OpenCASCADE PCurve终极问题
eryar@163.com
Abstract: Geometry Curves and Surfaces in BRep are parametric equations. So given a parametric space curve and a geometry surface can map to a 3d geometry curve. The parametric space curve is PCurve. When given a 3d geometry curve and surface, how to get the PCurve?
Keywords: OpenCASCADE, BRep, PCurve, Project, ProjLib
1 Introduction
看过《西游记》的对其中一些台词记忆深刻,像唐僧每次介绍自己时说“贫僧唐三藏,从东土大唐而来,去往西天拜佛取经。”一句话点明哲学的终极问题:我是谁?我从哪里来?我要到哪里去?纵观三藏的心路历程可知,他从来就知道自己是谁,不管取经路途多么艰辛困苦,他总是初心不改,志在其中。
在学习新东西的时候,也会经常会有这些问题。如XXX是什么,怎么定义的。怎么生成XXX?XXX有什么用?能把这三个问题回答清楚,新东西基本就掌握了。
本文主要来回答PCurve的这三个问题,即PCurve是什么?PCurve从哪里来?PCurve有什么用?帮助大家深入理解这个BRep表示法中的核心概念。
2 PCurve是什么
我们找到OpenCASCADE中的注释对PCurve的描述:A 2D curve associated to the curve on surface in the parametric space of the surface。字面意思是曲面上的一条三维曲线对应到曲面的参数空间中的一条二维曲线,即PCurve是Parametric Space Curve的缩写。也提醒我们BRep中几何的表达采用的是参数方程的形式,对于曲线是一个参数的方程C(u),而对于曲面是两个参数的方程S(u, v)。曲面的参数空间就是曲面参数方程的定义域,是二维空间。给定曲面参数空间一条线(即PCurve)根据曲面的参数方程总是能映射到得到一条模型空间的三维曲线或退化的曲线。
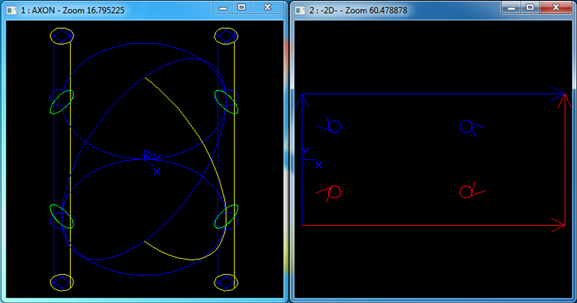
3 PCurve从哪里来
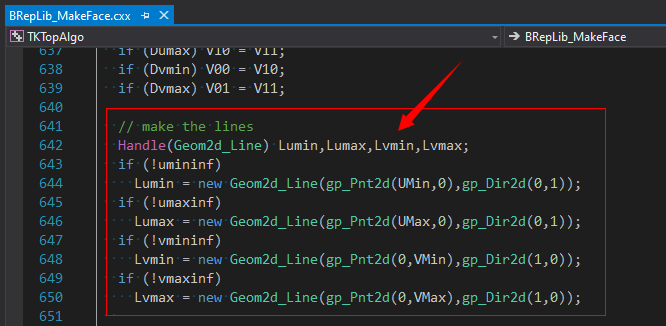
关于PCurve有两个要素:一是Curve,一是Surface。在生成Face的代码里,最关键的就是设置PCurve。从生成Face的类BRepLib_MakeFace中,我们可以看到,对于已经有参数范围的曲面,其PCurve就是参数范围在参数空间的一个矩形,这里是手动创建的。
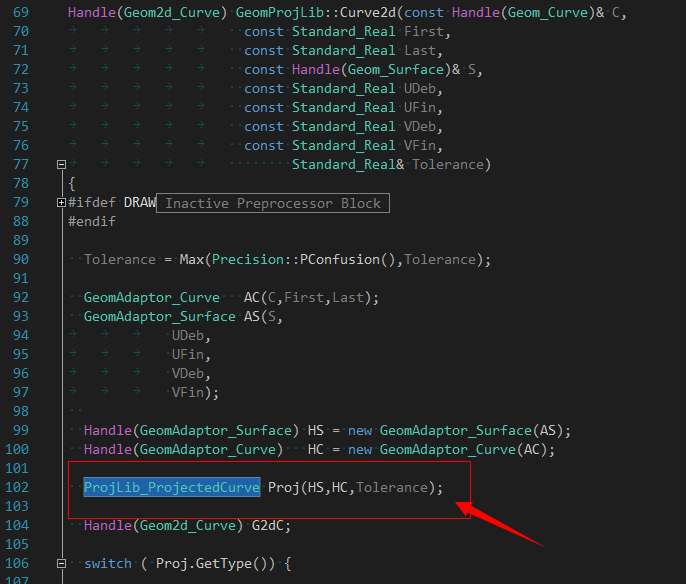
那更一般的情况怎么办呢?如已知曲面及曲面上的一条曲线,怎么得到PCurve?在OpenCASCADE中提供了一个静态函数来计算:

最终是调用类ProjLib_ProjectedCurve来计算的:
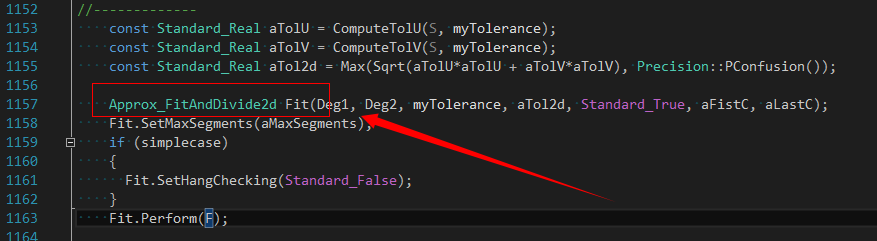
前面还介绍过了曲线向曲面投影的算法原理,知道是通过计算曲线上的点与曲面法向上的交点来求出曲面上的拟合曲线,这里的拟合曲线仍然是模型空间的三维曲线。那么怎么计算出曲线在曲面参数空间的PCurve呢?我们来看看类ProjLib_ComputeApprox,从中找出答案。
//=======================================================================
//function : Value
//purpose :
//=======================================================================
static gp_Pnt2d Function_Value(const Standard_Real U,
const Handle(Adaptor3d_Curve)& myCurve,
const Handle(Adaptor3d_Surface)& mySurface,
const Standard_Real U1,
const Standard_Real U2,
const Standard_Real V1,
const Standard_Real V2,
const Standard_Boolean UCouture,
const Standard_Boolean VCouture )
{
Standard_Real S = 0., T = 0.;
gp_Pnt P3d = myCurve->Value(U);
GeomAbs_SurfaceType SType = mySurface->GetType();
switch ( SType ) {
case GeomAbs_Plane:
{
gp_Pln Plane = mySurface->Plane();
ElSLib::Parameters( Plane, P3d, S, T);
break;
}
case GeomAbs_Cylinder:
{
gp_Cylinder Cylinder = mySurface->Cylinder();
ElSLib::Parameters( Cylinder, P3d, S, T);
break;
}
case GeomAbs_Cone:
{
gp_Cone Cone = mySurface->Cone();
ElSLib::Parameters( Cone, P3d, S, T);
break;
}
case GeomAbs_Sphere:
{
gp_Sphere Sphere = mySurface->Sphere();
ElSLib::Parameters(Sphere, P3d, S, T);
break;
}
case GeomAbs_Torus:
{
gp_Torus Torus = mySurface->Torus();
ElSLib::Parameters( Torus, P3d, S, T);
break;
}
default:
throw Standard_NoSuchObject("ProjLib_ComputeApprox::Value");
}
if ( UCouture) {
if(S < U1 || S > U2)
{
S = ElCLib::InPeriod(S, U1, U2);
}
}
if ( VCouture) {
if(SType == GeomAbs_Sphere) {
if ( Abs( S - U1 ) > M_PI ) {
T = M_PI - T;
S = M_PI + S;
}
if(S > U1 || S < U2)
S = ElCLib::InPeriod(S, U1, U2);
}
if(T < V1 || T > V2)
T = ElCLib::InPeriod(T, V1, V2);
}
return gp_Pnt2d(S, T);
}
上面是拟合PCurve的拟合函数,从拟合函数的定义可知,对于简单曲面上的曲线,给定参数U可以计算出曲线的点P3d,根据P3d计算出曲面的参数空间的参数S, T,最后将参数空间的点返回。即将这些参数空间的二维点进行拟合得到就是PCurve。
原来百思不得其解的问题终于有了头绪,可以看出这个方法还是很巧妙的。这里就回答了PCurve从哪来的问题:若你知道PCurve,可以自己手动设置;若对于任意曲面上曲线的PCurve,可以通过Project得到。从中可以看出拟合功能的重要性。
4 PCurve有什么用
从PCurve的定义上可以看出,通过PCurve相当于建立了Edge与Face的联系。从目前的理解来看PCurve主要还是用在Mesh,将Face网格化。因为网格化目前的算法主要还是在曲面的参数空间进行三角剖分:
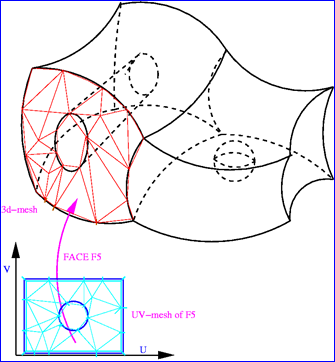
5 Conclusion
综上所述,在理解PCurve是什么后,大家可以自己思考下,如果让你实现生成PCurve的算法,你会怎么做呢?PCurve除了用于Mesh,还有哪些应用呢?期待大家的发掘。
理解PCurve后,相信OpenCASCADE的大部分源码大家已能看懂,为大家钻研源码打下基础。