OpenCASCADE Quaternion
eryar@163.com
Abstract. The quaternions are members of a noncommutative division algebra first invented by William Rowan Hamilton. The idea for quaternions occurred to him while he was walking along the Royal Cannal on his way to a meeting of the Irish Academy, and Hamilton was so pleased with his discovery that he scratched the fundamental formula of quaternion algebra. There are several different ways we can express orientation and angular displacement in 3D. Here we discuss the three most important methods-matrices, Euler angles, and quaternions.
Key Words. OpenCASCADE, Quaternion, Euler angles, Rotation, Transformation
1. Introduction
物体在三维空间中经常需要进行一些变换操作,如移动、旋转等。在CAD软件中如果提供的便利的交互方式来对模型的位置进行编辑,则软件的用户体验就很好。对模型位置编辑的结果需要在计算机中保存起来,这就需要用一种方式来记录模型的变换。如下图所示:
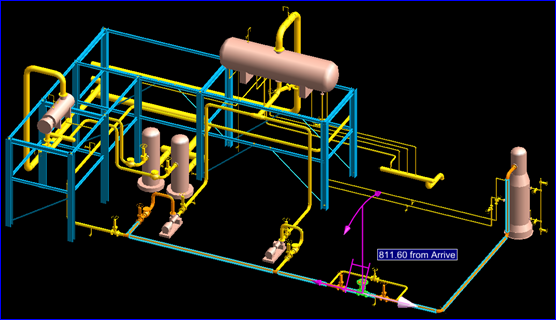
Figure 1.1 Modify the location of a Valve
上图所示为三维工厂软件PDMS中使用交互的方式来修改一个阀件的位置,直接使用鼠标拖动高亮的箭头即可实现对阀件位置的编辑。
物体在三维空间中的旋转变换操作常见的有三种表示方法:Matrix、Euler Angles、Quaternion。每种表示方式各用利弊,根据需要选择合适的旋转的表示方式。本文详细介绍了这三种方式及在OpenCASCADE中使用Quaternion和在这三种表示方式之间进行转换。
2.Rotation in Matrix Form
在3D空间中描述坐标系的方位(orientation)的一种方法就是列出这个坐标系的基向量,这些基向量是用其他的坐标系来描述的。用这些基向量构成一个3X3矩阵,然后就能用矩阵的形式来描述方位了。换句话说,能用一个旋转矩阵来描述这两个坐标系之间的相对方位,这个旋转矩阵用于把一个坐标系中的向量变换到另一个坐标系中,如下图所示:
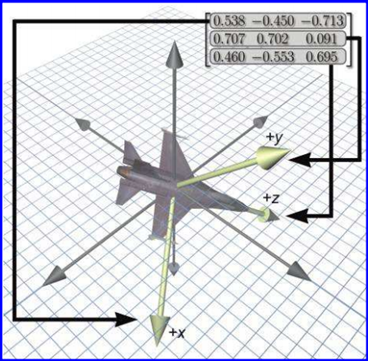
Figure 2.1 Defining an orientation using a matrix
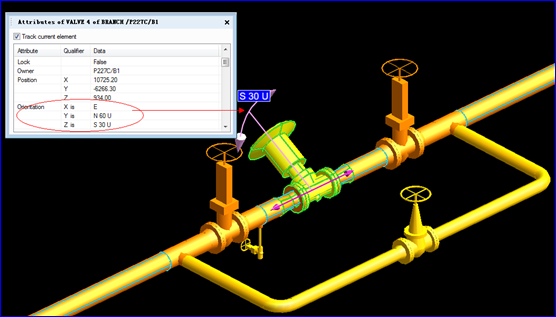
Figure 2.2 A Valve Orientation in PDMS
由上图可知,在PDMS中对模型的方位的保存也是采用了矩阵形式,其中X is E,Y is N 60U, Z is S 30 U这其实是三个向量。下面给出绕任意轴旋转一定角度的矩阵表示的证明:
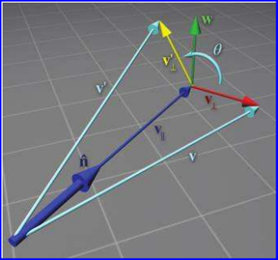
Figure 2.3 Rotating a vector about an arbitrary axis
根据向量的运算规则容易推出:
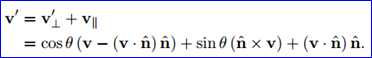
则绕轴旋转的矩阵形式如下:
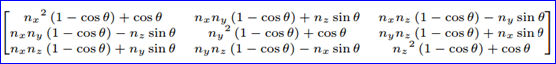
其中在OpenCASCADE的类gp_Mat中实现代码如下所示:
void gp_Mat::SetRotation (const gp_XYZ& Axis,
const Standard_Real Ang)
{
// Rot = I + sin(Ang) * M + (1. - cos(Ang)) * M*M
// avec M . XYZ = Axis ^ XYZ
// const Standard_Address M = (Standard_Address)&(matrix[0][0]);
gp_XYZ V = Axis.Normalized();
SetCross (V);
Multiply (sin(Ang));
gp_Mat Temp;
Temp.SetScale (1.0);
Add (Temp);
Standard_Real A = V.X();
Standard_Real B = V.Y();
Standard_Real C = V.Z();
Temp.SetRow (1, gp_XYZ(- C*C - B*B, A*B, A*C ));
Temp.SetRow (2, gp_XYZ( A*B, -A*A - C*C, B*C ));
Temp.SetRow (3, gp_XYZ( A*C, B*C, - A*A - B*B));
Temp.Multiply (1.0 - cos(Ang));
Add (Temp);
}
3.Rotation with Euler Angles
用Euler角的方式来表示旋转这项技术是以著名数学家Leonhard Euler(1707~1783)来命名的,他证明了角位移序列等价于单个角位移,即可以用一个合成的变换来表示多个连续的变换,证明过程详见苏步青《应用几何教程》。
Euler Angles的基本思想是将角位移分解为绕三个互相垂直的三个旋转组成的序列。这听起来有点复杂,其实是非常直观的,这也正是Euler Angle易于使用的优点之一。Euler Angle将方位Orientation分解为绕三个垂直轴的旋转,那么是哪三个轴?按什么顺序?其实任意三个轴和任意顺序都可以,但最有意义的是使用笛卡尔坐标系按一定顺序所组成的旋转序列。最常用的约定是所谓的“heading-picth-bank”,如下图所示为给定heading,picth和bank角度后,可以用四步法来确定Euler Angle对应的Orientation:
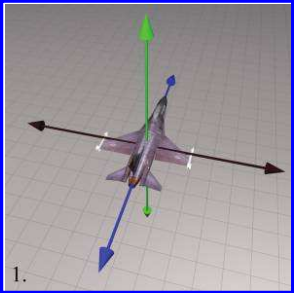
Figure 3.1 Step 1: An object in its identity orientation
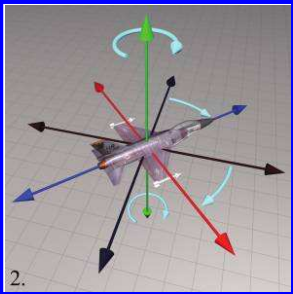
Figure 3.2 Step 2: Heading is the first rotation and rotates about the vertical axis(y-axis)
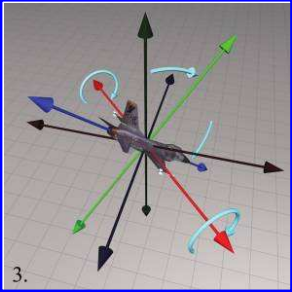
Figure 3.3 Step 3: Pitch is the second rotation and rotates about the object laterial axis(x-axis)
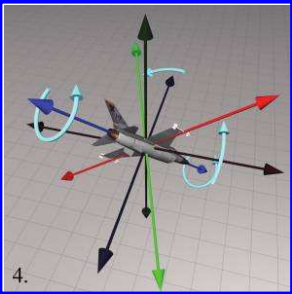
Figure 3.4 Step 4: Bank is the third and rotates about the object longitudinal axis(z-axis)
heading-pitch-bank系统不是唯一的Euler Angle系统。绕任意三个互相垂直的任意旋转序列都能定义一个方位orientation。所以多种选择导致了Euler Angle约定的多样性。如常用的术语roll-pitch-yaw,其中roll等价于bank,yaw基本上等价于heading,他的顺序与heading-pitch-bank相反。
因为Euler Angle的易用性,只需要约定旋转序列和三个角度即可表示方位了。可以仿照上述变换过程应用Euler Angle来实现模型旋转编辑的交互操作,实现交互方式友好的操作。即当鼠标移动到高亮的旋转handle上时,就可以绕一个轴旋转一定角度,不一定是按heading-pitch-bank的顺序来旋转。如下图所示:
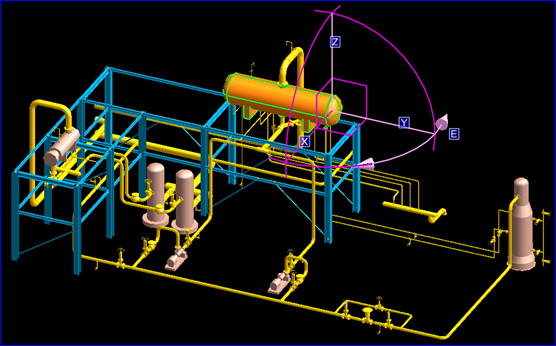
Figure 5. Model Editor in PDMS
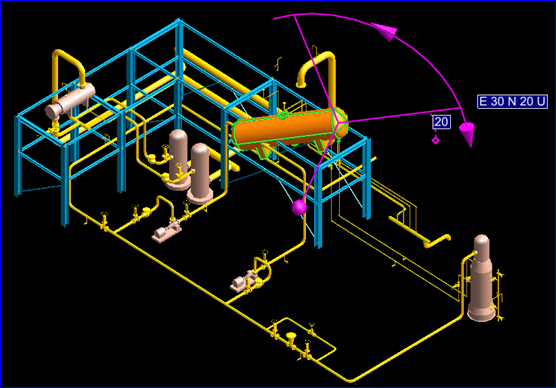
Figure 6. Euler Angle in Model Editor
由上图可知,对模型进行旋转时,实时显示的角度正是Euler Angle。如果约定了Euler Angle的顺序,如为heading-pitch-bank,只需要三个实数即可表示方位orientation,这在将方位数据保存到文件时有很大优势,可以节省大量存储空间。如下图所示:
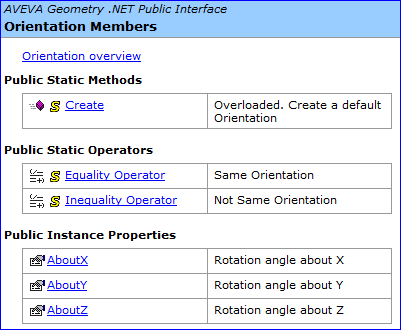
Figure 7. Orientation Properties in AVEVA Plant/PDMS
由上图可知,PDMS的数据库中保存orientation的方式使用了Euler Angle的方式,这样与矩阵的方式相比,数据量要少两倍,因为一般的模型都有这个属性,这样下来,节省的存储空间比较可观。
因为Euler Angles的方式最简单直观,就是三个角度,所以一般都是将Euler Angle转换到其他的形式,如Matrix和Quaternion。
4.Quaternions
一个Quaternion包含一个标量分量和一个3D向量分量,一般记标量分量为w,向量分量为V或分开的x,y,z,如Q=[w, V]或Q=[w,(x,y,z)]。
Quaternion能被解释为角位移的轴-角对方式。然而,旋转轴和角度不是直接存储在Quaternion的四个数中,它们的确在Quaternion中,但是不是那么直接,其关系式为:
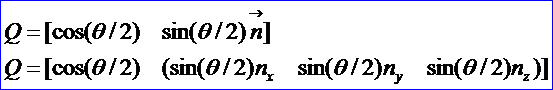
根据这个关系式即可实现绕轴旋转一定角度的Quaternion,其中OpenCASCADE中的实现代码如下所示:
//=======================================================================
//function : SetVectorAndAngle
//purpose :
//=======================================================================
void gp_Quaternion::SetVectorAndAngle (const gp_Vec& theAxis,
const Standard_Real theAngle)
{
gp_Vec anAxis = theAxis.Normalized();
Standard_Real anAngleHalf = 0.5 * theAngle;
Standard_Real sin_a = Sin (anAngleHalf);
Set (anAxis.X() * sin_a, anAxis.Y() * sin_a, anAxis.Z() * sin_a, Cos (anAngleHalf));
}
为了将Quaternion转换到矩阵形式,可以利用绕任意轴旋转的矩阵,公式如下所示:
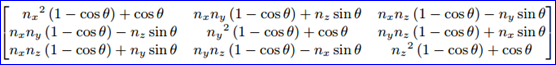
矩阵是由旋转轴n和旋转角度θ表示的,但是Quaternion是由下述分量表示的:
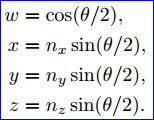
将R(n,θ)变换到R(w,x,y,z)是一个技巧性很强的推导,如果只是为了使用矩阵,那么就不必理解矩阵是如何推导的。如果对推导过程感兴趣,可参考Fletcher Dunn,Ian Parberry.所著《3D Math Primer for Graphics and Game Development》,其中有详细推导说明。下面就直接给出推导结果:
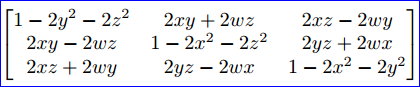
Figure 4.1 Converting a quaternion to a 3x3 matrix
在OpenCASCADE中取得Quaternion的矩阵数据是通过函数GetMatrix,其实现代码如下所示:
//=======================================================================
//function : GetMatrix
//purpose :
//=======================================================================
gp_Mat gp_Quaternion::GetMatrix () const
{
Standard_Real wx, wy, wz, xx, yy, yz, xy, xz, zz, x2, y2, z2;
Standard_Real s = 2.0 / SquareNorm();
x2 = x * s; y2 = y * s; z2 = z * s;
xx = x * x2; xy = x * y2; xz = x * z2;
yy = y * y2; yz = y * z2; zz = z * z2;
wx = w * x2; wy = w * y2; wz = w * z2;
gp_Mat aMat;
aMat (1, 1) = 1.0 - (yy + zz);
aMat (1, 2) = xy - wz;
aMat (1, 3) = xz + wy;
aMat (2, 1) = xy + wz;
aMat (2, 2) = 1.0 - (xx + zz);
aMat (2, 3) = yz - wx;
aMat (3, 1) = xz - wy;
aMat (3, 2) = yz + wx;
aMat (3, 3) = 1.0 - (xx + yy);
// 1 division 16 multiplications 15 addidtions 12 variables
return aMat;
}
由代码可知,即是对上述转换公式的直接实现。如其注释中所言,转换涉及到了1个除法、16个乘法、15个加法和12个变量。
OpenCASCADE中还实现了从Euler Angles转换到Quaternion的功能,实现代码如下所示:
//=======================================================================
//function : GetEulerAngles
//purpose :
//=======================================================================
void gp_Quaternion::GetEulerAngles (const gp_EulerSequence theOrder,
Standard_Real& theAlpha,
Standard_Real& theBeta,
Standard_Real& theGamma) const
{
gp_Mat M = GetMatrix();
gp_EulerSequence_Parameters o = translateEulerSequence (theOrder);
if ( o.isTwoAxes )
{
double sy = sqrt (M(o.i, o.j) * M(o.i, o.j) + M(o.i, o.k) * M(o.i, o.k));
if (sy > 16 * DBL_EPSILON)
{
theAlpha = ATan2 (M(o.i, o.j), M(o.i, o.k));
theGamma = ATan2 (M(o.j, o.i), -M(o.k, o.i));
}
else
{
theAlpha = ATan2 (-M(o.j, o.k), M(o.j, o.j));
theGamma = 0.;
}
theBeta = ATan2 (sy, M(o.i, o.i));
}
else
{
double cy = sqrt (M(o.i, o.i) * M(o.i, o.i) + M(o.j, o.i) * M(o.j, o.i));
if (cy > 16 * DBL_EPSILON)
{
theAlpha = ATan2 (M(o.k, o.j), M(o.k, o.k));
theGamma = ATan2 (M(o.j, o.i), M(o.i, o.i));
}
else
{
theAlpha = ATan2 (-M(o.j, o.k), M(o.j, o.j));
theGamma = 0.;
}
theBeta = ATan2 (-M(o.k, o.i), cy);
}
if ( o.isOdd )
{
theAlpha = -theAlpha;
theBeta = -theBeta;
theGamma = -theGamma;
}
if ( ! o.isExtrinsic )
{
Standard_Real aFirst = theAlpha;
theAlpha = theGamma;
theGamma = aFirst;
}
}
下面给出在OpenCASCADE中使用Quaternion的具体示例,代码如下所示:
/*
* Copyright (c) 2013 to current year. All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-11-29 10:18
* Version : OpenCASCADE6.8.0
*
* Description : Test OpenCASCADE quaternion.
*
* Key Words : OpenCASCADE, Quaternion
*
*/
#define WNT
#include <gp_Quaternion.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
void TestQuaternion(void)
{
gp_Quaternion aQuaternion;
// create quaternion by axis-angle.
aQuaternion.SetVectorAndAngle(gp_Vec(1.0, 0.0, 0.0), M_PI_2);
// convert quaternion to matrix.
gp_Mat aMatrix = aQuaternion.GetMatrix();
Standard_Real aYaw = 0.0;
Standard_Real aPitch = 0.0;
Standard_Real aRoll = 0.0;
// convert quaternion to Euler Angles.
aQuaternion.GetEulerAngles(gp_YawPitchRoll, aYaw, aPitch, aRoll);
}
int main(int argc, char* argv[])
{
TestQuaternion();
return 0;
}
5.Conclusions
综上所述,Euler Angles最容易被使用,当需要为世界中的物体指定方位时,Euler Angles能大简化人机交互,包括直接的键盘、鼠标输入及在调试中测试。
如果需要要坐标系之间进行转换向量,那么就选矩阵形式。当然这并不意味着你不能使用其他格式来保存方位,并在需要的时候转换到矩阵形式。另一种方法是用Euler Angles作为方位的“主拷贝”,并同时维护一个旋转矩阵,当Euler Angles发生变化时矩阵也同时进行更新。
当需要大量保存方位数据时,就使用Euler Angles或Quaternion。Euler Angles将少占用25%的空间,但它在转换到矩阵时要稍微慢点。如果动画数据需要进行坐标系之间的连接,Quaternion可能是最好的选择了。
平滑的插值只能用Quaternion来完成,这在OpenSceneGraph中有大量的应用。如果你使用其他形式,也可先转换成Quaternion再进行插值,插值完成后再转换回原来的形式。
OpenCASCADE的Quaternion类中实现了Matrix, Euler Angles的转换,即通过gp_Quaternion即可将旋转操作在这三种形式之间进行转换。
6. References
1. WolframMathWorld, http://mathworld.wolfram.com/Quaternion.html
2. Ken Shoemake. Conversion between quaternion and Euler angles. Graphics Gems IV, P222-22
http://tog.acm.org/resources/GraphicsGems/gemsiv/euler_angle/EulerAngles.c
3. 苏步青, 华宣积. 应用几何教程. 复旦大学出版计. 2012
4. 丘维声. 解析几何. 北京大学出版社. 1996
5. 同济大学应用数学系编. 线性代数(第四版). 高等教育出版社. 2003
6. Fletcher Dunn,Ian Parberry. 3D Math Primer for Graphics and Game Development. CRC Press
7. 史银雪,陈洪,王荣静. 3D数学基础:图形与游戏开发. 清华大学出版社. 2005
8. 苏步青. 神奇的符号. 湖南少年儿童出版社. 2010