1. Plot B-Spline Basis Function
When draw Bezier curve, you only need to know Bernstein basis function, life was easier.Bernstein basis function solely as a function of the number of control points. Now you have a lot more flexibility, but you also have a lot more to worry about. In addition to control points, the B-Spline basis function must account for the degree of the cruve, as well as the ranges defined by the knot vector. The resulting basis functions are defined not by Bernstein polynomials, but by the Cox-de Boor recursion formulas. [Ref. : Focus on Cruves and Surfaces]
当画Bezier曲线时,事情要简单些,因Bezier曲线由Bernstein基函数确定,而Bernstein基函数只与控制顶点数有关。当画B-Spline曲线时,有了更多的灵活性,即有了局部修改能力,但是你需要考虑的事就更多了。除了控制顶点外,B-Spline曲线的基函数必须解释曲线的次数和节点矢量定义的范围。即B-Spline曲线的基函数由Cox-de Boor递归方法定义:
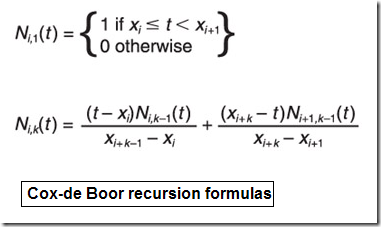
Imagine I want to draw a fourh-order(k=4) cubic curve with 4 control points and I choose a knot vector of [x]=[0,0,0,0,1,1,1,1]. The knot vector forces each control point to affect the entire curve.
假如我想画一个四个控制顶点形成的四阶三次曲线,选择节点矢量为[x]=[0,0,0,0,1,1,1,1]。节点矢量迫使每个控制顶点的改变影响到整个曲线。
使用B样条基函数的递归公式画出各阶基函数的图形。MATLAB代码如下:
1: %-------------------------------------------------------------------------
2: % Imagine I want to draw a fourth-order cubic curve with 4 control points
3: % and I choose a knot vector of [x]=[0,0,0,0,1,1,1,1].
4: %-------------------------------------------------------------------------
5:
6: t=0:0.01:1; % knot vector range
7:
8: %-------------------------------------------------------------------------
9: % 1. First-order basis functions for k=4 [x]=[0,0,0,0,1,1,1,1]
10: % N11=0;
11: % N21=0;
12: % N31=0;
13: % N41=1;
14: %-------------------------------------------------------------------------
15:
16: N11=0;
17: N21=0;
18: N31=0;
19: N41=1;
20:
21: subplot(2,2,1);
22: plot(t,N11,t,N21,t,N31,t,N41);
23:
24: %-------------------------------------------------------------------------
25: % 2. Second-order basis functions for k=4 [x]=[0,0,0,0,1,1,1,1]
26: % N12=0;
27: % N22=0;
28: % N32=1-t;
29: % N42=t;
30: %-------------------------------------------------------------------------
31:
32: N12=0;
33: N22=0;
34: N32=1-t;
35: N42=t;
36:
37: subplot(2,2,2);
38: plot(t,N12,t,N22,t,N32,t,N42)
39:
40: %-------------------------------------------------------------------------
41: % 3. Third-order basis functions for k=4 [x]=[0,0,0,0,1,1,1,1]
42: % N13=0;
43: % N23=(1-t)^2;
44: % N33=2t(1-t);
45: % N43=t^2;
46: %-------------------------------------------------------------------------
47:
48: N13=0;
49: N23=(1-t).^2;
50: N33=2*t.*(1-t);
51: N43=t.^2;
52:
53: subplot(2,2,3);
54: plot(t,N13,t,N23,t,N33,t,N43);
55:
56: %-------------------------------------------------------------------------
57: % 4. Fourth-order basis functions for k=4 [x]=[0,0,0,0,1,1,1,1]
58: % N14=(1-t)^3;
59: % N24=3t(1-t)^2;
60: % N34=3(1-t)t^2;
61: % N44=t^3;
62: %-------------------------------------------------------------------------
63:
64: N14=(1-t).^3;
65: N24=3*t.*(1-t).^2;
66: N34=3*(1-t).*t.^2;
67: N44=t.^3;
68:
69: subplot(2,2,4);
70: plot(t,N14,t,N24,t,N34,t,N44);
.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }
用MATLAB画出各阶基函数如下图所示:
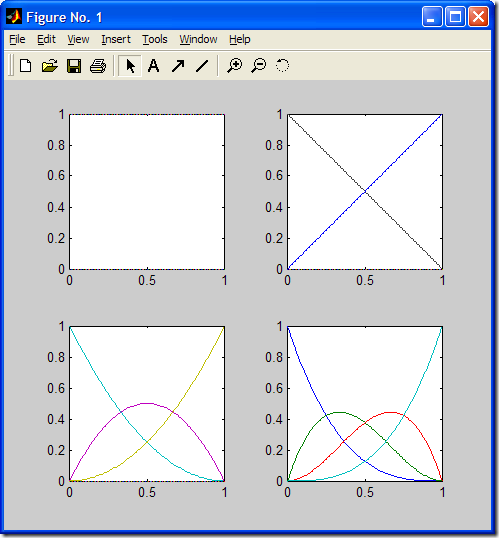
三次均匀B样条基函数Ni,3(u)的图形由MATLAB生成如下所示:
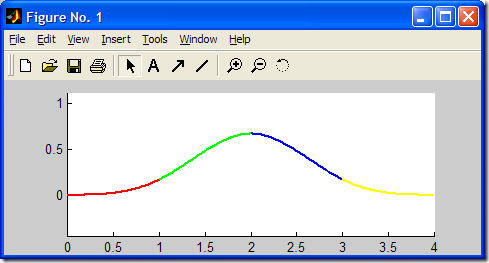
生成此图形的MATLAB代码如下:
1: %------------------------------------------------------------------------------
2: % 均匀B样条基最简单的形式是取节点为整数:Ti=i(i=0,1,2,...,n),
3: % 令:t-ti=u,则参数u的取值范围为[0,1]。则得Ni,3(u)如下式:
4: % | u^3 / 6; u=[0,1]
5: % | (-3u^3 + 3u^2 + 3u + 1) / 6; u=[0,1]
6: % Ni,3(u) = | (3u^3 - 6u^2 + 4) / 6; u=[0,1]
7: % | (-u^3 + 3u^2 - 3u + 1) / 6; u=[0,1]
8: %
9: %------------------------------------------------------------------------------
10:
11: u=0:0.01:1;
12: N03=u.^3/6;
13: N13=(-3*u.^3 + 3*u.^2 + 3*u + 1)/6;
14: N23=(3*u.^3 - 6*u.^2 + 4) / 6;
15: N33=(-u.^3 + 3*u.^2 - 3*u + 1) / 6;
16:
17: line(u, N03, 'Color', 'r');
18: line(u+1, N13, 'Color', 'g');
19: line(u+2, N23, 'Color', 'b');
20: line(u+3, N33, 'Color', 'y');
.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }
2. Plot B-Spline Curve
已知平面上五个顶点矢量V0(0,1), V1(1,1), V2(1,0), V3(1,-1), V4(2,-1), 要求构造一条三次均匀B样条曲线,并做出图形.
使用MATLAB代码如下:
1: %-----------------------------------------------------------
2: % Plot Cubic Uniform B-Spline Curve.
3: % Just for Testing, Welcome your advice: eryar@163.com
4: %
5: % Date : 2011-12-28 21:31
6: %
7: %-----------------------------------------------------------
8:
9: % Knot Vector range.
10: u=0:0.01:1;
11:
12: % Control Points.
13: % You can change the control point's number and value
14: % to test the effect.
15: V0=[0 1];
16: V1=[1 1];
17: V2=[1 0];
18: V3=[1 -1];
19: V4=[2 -1];
20:
21: % Basis Functions.
22: N03=(-u.^3 + 3*u.^2 - 3*u + 1) / 6;
23: N13=(3*u.^3 - 6*u.^2 + 4) / 6;
24: N23=(-3*u.^3 + 3*u.^2 + 3*u + 1)/6;
25: N33=u.^3/6;
26:
27: % Calculate every segment.
28: r0x=N03 * V0(1) + N13 * V1(1) + N23 * V2(1) + N33 * V3(1);
29: r0y=N03 * V0(2) + N13 * V1(2) + N23 * V2(2) + N33 * V3(2);
30: r1x=N03 * V1(1) + N13 * V2(1) + N23 * V3(1) + N33 * V4(1);
31: r1y=N03 * V1(2) + N13 * V2(2) + N23 * V3(2) + N33 * V4(2);
32:
33: % Plot the Control Polygon.
34: plot(V0(1), V0(2), 'Marker', 'o'); hold on;
35: plot(V0(1), V0(2), 'Marker', 'o'); hold on;
36: plot(V1(1), V1(2), 'Marker', 'o'); hold on;
37: plot(V2(1), V2(2), 'Marker', 'o'); hold on;
38: plot(V3(1), V3(2), 'Marker', 'o'); hold on;
39:
40: % Plot the Uniform B-Spline Curve.
41: line('XData', r0x, 'YData', r0y, 'Color', 'r'); 42: line('XData', r1x, 'YData', r1y, 'Color', 'g');
.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }
生成图形如下所示:
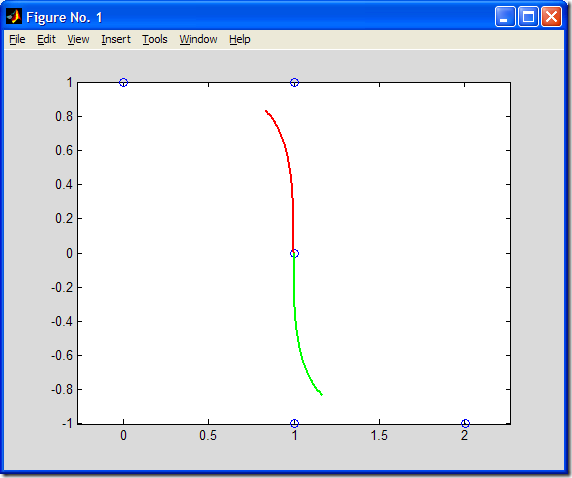
如图所示,B样条曲线由两段组成,控制顶点由“0”标出。
试求由特征顶点V0=[-1,1], V1=[1,1], V2=[1,-1], V3=[-1,-1]决定的闭合的三次均匀B样条曲线,并做出图形。适当修改上述MATLAB代码,即可得到所求B样条曲线,如下图所示:
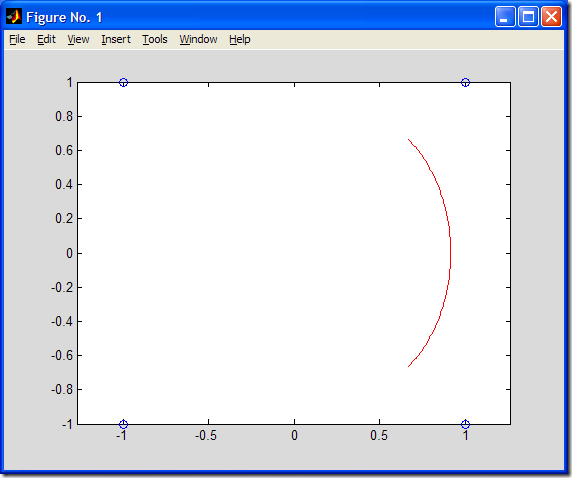
3.结论:
对于均匀B样条基函数,由于节点矢量均匀递增,所以在每两个节点组成的区间的距离相等。利用基函数的的递推公式可以计算出每个区间上的函数表达式。对于上例中的均匀B样条基每个区间取值范围都是从0到1,通过偏移X轴,可画出B样条的基函数。
通过MATLAB画出B样条曲线的基函数,操作简单,便于对B样条基函数的理解。在理解B样条基函数后,会对B样条曲线的理解更加深刻。继续加油!!