A*在游戏寻路算法里使用很广,可是感觉很多介绍它的文章故意让人看不懂。
仔细看了看gamedev.net的一片文章(
A* Pathfinding for Beginners
http://www.gamedev.net/reference/articles/article2003.asp
),对A*更了解了一点,写点东西记录一下。
A*是一种启发式的算法,所谓的"启发式",就是对每一个搜索的位置进行评估,也就是把找的位置离目标的距离当成找点的一个依据,然后猜测这个点是否最佳("启发式"就是猜测)。
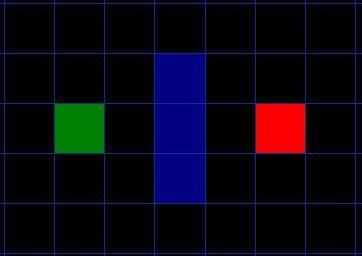
为了找到最佳的那个点
可以规定:
G = 从起点,沿着产生的路径,移动到网格上指定方格的距离。
H = 从网格上那个方格移动到终点B的预估移动距离。
F = G + H
F最小的点可以认为是该选的点。
引用一下原文的翻译:
我们令水平或者垂直移动的耗费为10,对角线方向耗费为14。我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号2(别怕),或者约1.414倍。为了简化,我们用10和14近似。比例基本正确,同时我们避免了求根运算和小数。
既然我们在计算沿特定路径通往某个方格的G值,求值的方法就是取它父节点的G值,然后依照它相对父节点是对角线方向或者直角方向(非对角线),分别增加14和10。例子中这个方法的需求会变得更多,因为我们从起点方格以外获取了不止一个方格。
H值可以用不同的方法估算。我们这里使用的方法被称为曼哈顿方法,它计算从当前格到目的格之间水平和垂直的方格的数量总和,忽略对角线方向。然后把结果乘以10。这被成为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数,在那里你不能沿对角线方向穿过街区。很重要的一点,我们忽略了一切障碍物。这是对剩余距离的一个估算,而非实际值,这也是这一方法被称为启发式的原因。想知道更多?你可以在这里找到方程和额外的注解。
第一步搜索的结果可以在下面的图表中看到。F,G和H的评分被写在每个方格里。正如在紧挨起始格右侧的方格所表示的,F被打印在左上角,G在左下角,H则在右下角。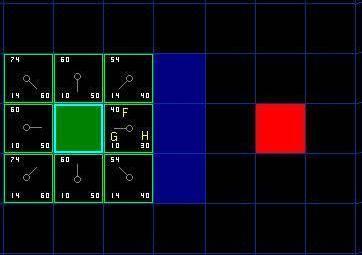
引用一下原文的翻译:
我们做如下操作开始搜索:
1,从点A开始,并且把它作为待处理点存入一个“开启列表”。开启列表就像一张购物清单。尽管现在列表里只有一个元素,但以后就会多起来。你的路径可能会通过它包含的方格,也可能不会。基本上,这是一个待检查方格的列表。
2,寻找起点周围所有可到达或者可通过的方格,跳过有墙,水,或其他无法通过地形的方格。也把他们加入开启列表。为所有这些方格保存点A作为“父方格”。当我们想描述路径的时候,父方格的资料是十分重要的。后面会解释它的具体用途。
3,从开启列表中删除点A,把它加入到一个“关闭列表”,列表中保存所有不需要再次检查的方格。
为了继续搜索,我们简单的从开启列表中选择F值最低的方格。然后,对选中的方格做如下处理:
4,把它从开启列表中删除,然后添加到关闭列表中。
5,检查所有相邻格子。跳过那些已经在关闭列表中的或者不可通过的(有墙,水的地形,或者其他无法通过的地形),把他们添加进开启列表,如果他们还不在里面的话。把选中的方格作为新的方格的父节点。
6,如果某个相邻格已经在开启列表里了,检查现在的这条路径是否更好。换句话说,检查如果我们用新的路径到达它的话,G值是否会更低一些。如果不是,那就什么都不做。
另一方面,如果新的G值更低,那就把相邻方格的父节点改为目前选中的方格(在上面的图表中,把箭头的方向改为指向这个方格)。最后,重新计算F和G的值。如果这看起来不够清晰,你可以看下面的图示。
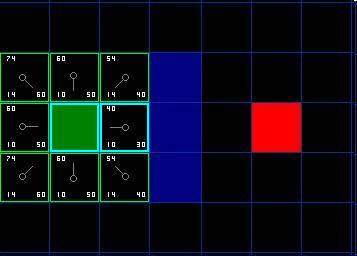
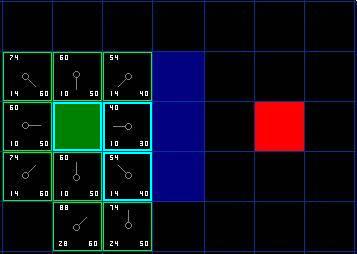
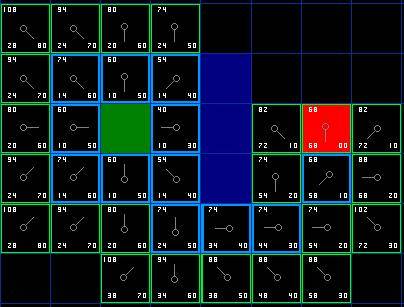
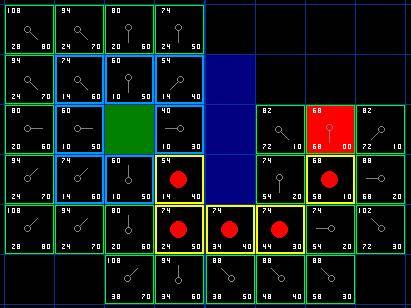
这样就可以找到最佳路径了。