一年十二月谁主春秋关注：基础系统工程密码学人工智能 - C++博客

随笔-166 评论-223 文章-30 trackbacks-0

关于格的行列式之解释

先摘自文献[1]中Lattice-based Cryptography章节引用的结论

再对上文三个结论稍作证明如下

参考文献

[1] Post-Quantum Cryptography

[2] 算法数论裴定一祝跃飞

[3] 高等代数丘维声

posted @ 2026-03-04 16:41 春秋十二月阅读(92) | 评论 (0) | 编辑收藏

NTRU格密码一处恒等式的证明

先摘取文献[1]的NTRU密码算法描述

矩阵T及T^*的定义如下

再给出证明过程

参考文献
[1] Post-Quantum Cryptography

posted @ 2026-01-27 18:00 春秋十二月阅读(93) | 评论 (0) | 编辑收藏

关于线性码的主要结论及应用

符号定义

主要结论

在密码学中的应用

上述McEliece公钥算法成立的关键之一是G^pub=SGP。由前面的定理1可得出G^pub与G等价，
但隐藏了码结构，另由于矩阵分解G^pub得到S和P是困难的，因为P随机且LU分解变形不唯一，
当n和t较大时，Goppa码的生成矩阵是天文数字。从而增加了密码分析的难度

上述红色下划线处的结论，其根据是推论1

这里的线性码下界定义本质跟定理7一样，从校验矩阵H的所有列向量中，选取0个向量（即向量0）生成的线性组合数 +
选取1个线性无关向量生成的线性组合数 + 选取2个无关向量生成的线性组合数 + … +
选取d₀-1个无关向量生成的线性组合数，不超过r个无关向量生成的线性组合总数。下面解释了红色下划线处的结论

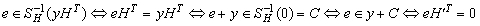
参考文献

[1] 高等代数丘维声

[2] Finite fields Rudolf Lidl Harald Niederreiter

[3] Post-Quantum Cryptography

posted @ 2026-01-25 20:30 春秋十二月阅读(116) | 评论 (0) | 编辑收藏

关于LLL算法的补充证明

先摘录文献[1]中的LLL算法描述流程，及LLL约化基的定义

LLL约化基的定义如下（文献[1]定义13.12）

再证明上图红色方框三行伪代码的正确性（其它部分文献[1]已讲得比较具体）

参考文献

[1] 算法数论裴定一祝跃飞

[2] 高等代数丘维声

posted @ 2025-09-28 17:43 春秋十二月阅读(383) | 评论 (0) | 编辑收藏

关于分圆域的一般结论

参考文献

[1]代数与数论李超周悦

[2]抽象代数II 徐明曜赵春来

posted @ 2025-07-28 12:01 春秋十二月阅读(460) | 评论 (0) | 编辑收藏

一个欧拉数整除问题的两种证法

参考文献

[1] 代数学基础与有限域林东岱

[2] 抽象代数赵春来徐明曜

posted @ 2025-06-20 18:41 春秋十二月阅读(575) | 评论 (0) | 编辑收藏

有限域上的特征与指数和之扩展

符号含义

关于特征的结论

关于指数和的结论

参考文献

[1] 代数学基础与有限域林东岱

[2] 代数与数论李超周悦

[3] 关于群的一些结论及应用本人

posted @ 2025-06-05 09:30 春秋十二月阅读(270) | 评论 (0) | 编辑收藏

二元二次型的相似变换、正定性与正交分解

本文主要阐述用两种方法判断给定两个二元二次型是否相似，相似情况下的具体变换。
相似变换如果确定了，也利于判断正定性，因为相似二次型的正定性相同。最后讲到了正交分解，
给出怎么求相似的整数对角矩阵

基本定义

下述定义来自文献[1] 12.1节，有所扩展

变换求解

先来看运用解方程的方法

再来看用矩阵的观点方法，求解变换。这种方法更适合求解到对角型的变换

正交分解

参考文献

[1] 华罗庚文集数论卷2

[2] 高等代数丘维声

posted @ 2025-04-25 19:05 春秋十二月阅读(403) | 评论 (0) | 编辑收藏

关于群的一些结论及应用

【命题1】所有群同态的原像个数相同，即为核的大小

下面看下这个结论在文献[1]中3.2节的应用

【命题2】所有元素阶小于等于2 的群为交换群，且其阶为2的整数幂

该结论在https://zhuanlan.zhihu.com/p/644888274中的推论2.2证明中用到

【命题3】群中任一元的相对于正规子群的指数次幂属于正规子群，2阶正规子群必

属于群的中心

【定理1】模奇合数的既约乘法群，其中雅可比符号为1的元素构成它的子群，其阶为

既约乘法群群阶的一半

【定理2】设G是群，H、K是有限子群，则HK的大小等于H的阶与K的阶乘积除以H与K交群的阶

参考文献

[1] 椭圆曲线及其在密码学中的应用—导引 Andreas Enge

[2] 抽象代数I 赵春来徐明曜
[3] 华罗庚文集数论卷2

[4] 组合数学冯荣权宋春伟

posted @ 2025-04-22 21:18 春秋十二月阅读(403) | 评论 (0) | 编辑收藏

不定方程的代数数论解法

符号含义与适用前提

二次域的基本结论

x²-dy²=±1

x² + d = y³

x² + y² = n

参考文献
[1] 代数与数论李超周悦

posted @ 2024-12-23 11:33 春秋十二月阅读(420) | 评论 (0) | 编辑收藏

仅列出标题