http://en.wikipedia.org/wiki/Taylor_series

Taylor series in several variables

The Taylor series may also be generalized to functions of more than one variable with

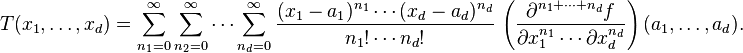
T(x_1,\dots,x_d) = \sum_{n_1=0}^\infty \sum_{n_2=0}^\infty \cdots \sum_{n_d = 0}^\infty \frac{(x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d}}{n_1!\cdots n_d!}\,\left(\frac{\partial^{n_1 + \cdots + n_d}f}{\partial x_1^{n_1}\cdots \partial x_d^{n_d}}\right)(a_1,\dots,a_d).\!

For example, for a function that depends on two variables, x and y, the Taylor series to second order about the point (a, b) is:

\begin{align} f(x,y) & \approx f(a,b) +(x-a)\, f_x(a,b) +(y-b)\, f_y(a,b) \\ & {}\quad + \frac{1}{2!}\left[ (x-a)^2\,f_{xx}(a,b) + 2(x-a)(y-b)\,f_{xy}(a,b) +(y-b)^2\, f_{yy}(a,b) \right], \end{align}

where the subscripts denote the respective partial derivatives.

A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as

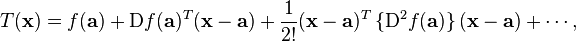
T(\mathbf{x}) = f(\mathbf{a}) + \mathrm{D} f(\mathbf{a})^T (\mathbf{x} - \mathbf{a}) + \frac{1}{2!} (\mathbf{x} - \mathbf{a})^T \,\{\mathrm{D}^2 f(\mathbf{a})\}\,(\mathbf{x} - \mathbf{a}) + \cdots\! \,,

where 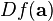D f(\mathbf{a})\! is the gradient of 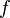\,f evaluated at 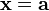\mathbf{x} = \mathbf{a} and D^2 f(\mathbf{a})\! is the Hessian matrix. Applying the multi-index notation the Taylor series for several variables becomes

T(\mathbf{x}) = \sum_{|\alpha| \ge 0}^{}\frac{(\mathbf{x}-\mathbf{a})^{\alpha}}{\alpha !}\,({\mathrm{\partial}^{\alpha}}\,f)(\mathbf{a})\,,

which is to be understood as a still more abbreviated multi-index version of the first equation of this paragraph, again in full analogy to the single variable case.

[edit]Example

Second-order Taylor series approximation (in gray) of a function f(x,y) = e^x\log{(1+y)}around origin.

Compute a second-order Taylor series expansion around point (a,b) = (0,0) of a function

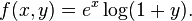
f(x,y)=e^x\log(1+y).\,

Firstly, we compute all partial derivatives we need

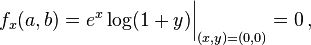
f_x(a,b)=e^x\log(1+y)\bigg|_{(x,y)=(0,0)}=0\,,
f_y(a,b)=\frac{e^x}{1+y}\bigg|_{(x,y)=(0,0)}=1\,,
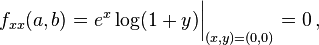
f_{xx}(a,b)=e^x\log(1+y)\bigg|_{(x,y)=(0,0)}=0\,,
f_{yy}(a,b)=-\frac{e^x}{(1+y)^2}\bigg|_{(x,y)=(0,0)}=-1\,,
f_{xy}(a,b)=f_{yx}(a,b)=\frac{e^x}{1+y}\bigg|_{(x,y)=(0,0)}=1.

The Taylor series is

\begin{align} T(x,y) = f(a,b) & +(x-a)\, f_x(a,b) +(y-b)\, f_y(a,b) \\ &+\frac{1}{2!}\left[ (x-a)^2\,f_{xx}(a,b) + 2(x-a)(y-b)\,f_{xy}(a,b) +(y-b)^2\, f_{yy}(a,b) \right]+ \cdots\,,\end{align}

which in this case becomes

\begin{align}T(x,y) &= 0 + 0(x-0) + 1(y-0) + \frac{1}{2}\Big[ 0(x-0)^2 + 2(x-0)(y-0) + (-1)(y-0)^2 \Big] + \cdots \\ &= y + xy - \frac{y^2}{2} + \cdots. \end{align}

Since log(1 + y) is analytic in |y| < 1, we have

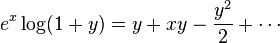
e^x\log(1+y)= y + xy - \frac{y^2}{2} + \cdots

for |y| < 1.