【适用前提】大整数N=pq的素因子p<q<2p,解密指数d<(1/3)N
1/4
【攻击方法】 1)用欧几里得算法计算e/N的各个渐近分数k
i/d
i,i>=1,直至d
i>=(1/3)N
1/4,记录此时的i为m。令i=1
2)计算T=(e*d
i-1)/k
i,若T不为整数则转到4),否则转到3)
3)解方程f(x)=x
2-(N-T+1)x+N=0的根,如果有正整数根且两个根皆小于N,则输出p、q,并返回成功。否则转到4)
4)递增i,若i<m则转回2),否则返回失败
该方法即
Wiener算法用到了关于连分数的一个
定理:若α为任一实数,有理数p/q适合|α-(p/q)|<1/(2q2),则p/q必为α的某一渐近分数。证明详见参考文献[2]。
由定理可知攻击方法是可行的,必能找到使f(x)=0有合理解的某渐近分数。下面证明:攻击迭代次数的上界为
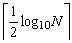 【证明】
【证明】

【例子】N = 9449868410449,e = 6792605526025,d<(1/3)N
1/4≈584,试分解N
 参考文献
参考文献
[1] 公钥密码学的数学基础 王小云、王明强、孟宪萌
[2] 算法数论 裴定一、祝跃飞
posted on 2024-04-04 18:19
春秋十二月 阅读(680)
评论(0) 编辑 收藏 引用 所属分类:
Algorithm