【定义】设整数N=P×Q，P与Q皆为素数，如果P≡Q≡3 (mod4)，则N为一个Blum（布卢姆）数

【定理】设N为Blum数，N ∤ d，若同余方程x²≡d (mod N)有解，则d的平方根中有一半的Jacobi符号为1，另一半Jacobi符号为-1；且仅有一个平方根为模N的二次剩余
    证明：
    

【推论】设N为Blum数，N=P×Q，令
    
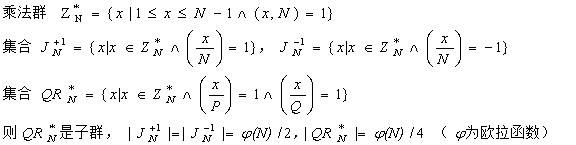   证明：
    

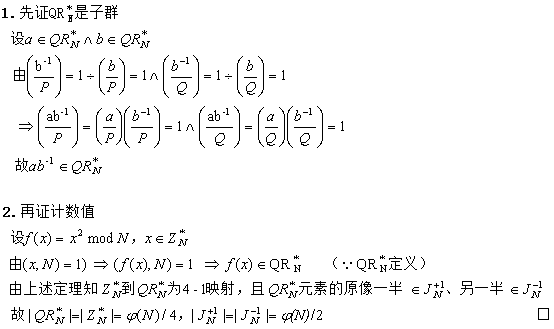【例子】由定义知N=21=3×7为Blum数，则相关乘法群、二次剩余子群、Jacobi集合如下
   


【应用一】Blum-Goldwasser公钥加密
      
    解密正确性是因为步骤1用到了欧拉定理及求平方根的如下算法，步骤2用到了中国剩余定理

       
       从上可得x=s^(P+1)/4 mod P或x=P-s^(P+1)/4 mod P，因(-1)^(P-1)/2等于-1 mod P，故前者为模P的二次剩余。从加密流程可知{s₁,s₂,...,s_n+1}正是模N二次剩余类的子集。
    所以从密文中r=s_n+1求它的(p+1)/4次幂、(q+1)/4次幂，迭代n次就得到了s₁模p的解、s₁模q的解，又因p、q、n在迭代中不变，故用欧拉定理预计算d_p mod (p-1)、d_q mod (q-1)。
    另一种（不太高效而直接的）解密如下
       
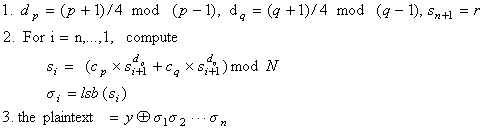
    另加密与明文异或的那部分实际是伪随机比特发生器，因为平方模N构成二次剩余类上的单向陷门置换，其最低有效位是核心断言，故从s_i+1求出lsb(s_i)是不可行的。简单证明如下
       
      由于均匀选择一个种子s₀，所以为概率加密，进而由可证明安全定理（每个概率公钥加密都是多项式安全的，及每个多项式安全的公钥加密都是语义安全的）知满足IND-CPA安全性
    易知IND-CCA2安全性是不满足的，因为敌手可用如下攻击方法获取明文：已知目标密文C=(r, m⊕σ₁σ₂⋯σ_n)，构造新密文C’=(r, m’⊕m⊕σ₁σ₂⋯σ_n)，将C’发给解密预言机得到m’’，则m=m’’⊕m’。
    由于加密产生的r与σ₁σ₂⋯σ_n都是伪随机的，所以密文(r, x⊕σ₁σ₂⋯σ_n)的分布是伪随机的，在目标密文前的解密询问会得到若干密文与明文对，无论怎么构造一对明文，任选其一加密得到的密文都不可区分。因此IND-CCA1安全性是满足的

【应用二】无爪函数/置换构造
      
      
    如上构造用到Blum数的上述推论，及基于大整数因子分解的困难假设。这里主要解释下为什么由两个Jacobi符号不同的平方根可计算大整数的素因子
      

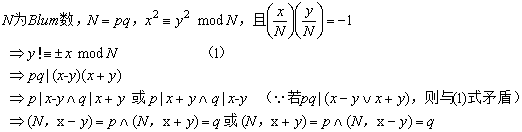【应用三】伪随机数发生器
                X_n+1=X_n² mod N      n=0、1、2...，X₀为种子
     显然种子不为1。若为一个非二次剩余，则从X₁开始就为二次剩余子群的元素，但最后必回到X₁而非X_0；若为二次剩余，则为了安全需要考究随机数数列的周期是否整周期（二次剩余子群的大小减1）。
  下面具体分析周期。先举例几个很小的Blum数
      
     从上面例子可以发现，由二次剩余子群构成的随机数数列不一定是整周期的，对于N=33无论种子怎么选，都是整周期4；对于N=57若种子选-8或7则周期为2，选其它则为6。
  现在一般化考虑，什么情况下才产生整周期？论证如下