变换的组合
设想世界中有一个任意方向、任意位置的物体,我们要把它渲染到任意方向、任意位置的摄像机中。为了做到这一点,必须将物体的所有顶点从物体坐标系变换到世界坐标系,接着再从世界坐标系变换到摄像机坐标系。其中的数学变换总结如下:

矩阵乘法满足结合律,所以我们能用一个矩阵直接从物体坐标系变换到摄像机坐标系:
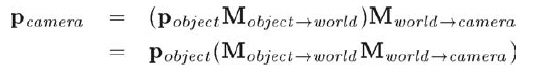
这样就能在渲染的循环外先将所有矩阵组合起来,使循环内作矩阵乘法的时候只需要和一个矩阵相乘即可(物体有很多顶点,省一次矩阵乘法就会提高不少效率),如下:

所以矩阵组合从代数角度看是利用了矩阵乘法的结合律。矩阵的行向量就是变换后的基向量,这在多个变换的情况下也是成立的。考虑矩阵乘法AB,结果中的每一行都是A中相应的行与矩阵B相乘的结果。换言之,设a1,
a2, a3为A的行,矩阵乘法能够写为:
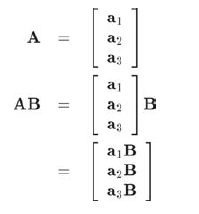
这使得结论更加清晰,AB结果中的行向量确实是对A的基向量进行B变换的结果。
变换分类
变换的类别并不是互斥的,也不存在一定的“次序”或“层次”使得某一类比另一类多或少一些限制。
当讨论一般意义上的变换时,我们将使用类似的术语:映射或函数。在最一般的意义上,映射就是一种简单的规则,接受输入,产生输出。我们把从a到b的F映射记作F(a)
= b。
线性变换
在数学上,如果满足下式,那么映射F(a)就是线性的:
F(a + b) = F(a) + F(b) 以及
F(ka) = kF(a)
如果映射F保持了基本运算:加法和数量乘,那么就可以称该映射为线性的。在这种情况下,将两个向量相加然后再进行变换得到的结果和先分别进行变换再将变换后的向量相加得到的结果相同。同样,将一个向量数量乘再进行变换和先进行变换再数量乘的结果也是一样的。
这个线性变换的定义有两条重要的引理:
(1) 映射F(a)
= aM,当M为任意方阵时,说映射是一个线性变换,这是因为:
F(a + b) = (a + b)M
= aM + bM = F(a) + F(b)
和
F(ka) = (ka)M = k(aM) =
kF(a)
(2) 零向量的任意线性变换的结果仍然是零向量。(如果F(0)
= a,a ≠ 0。那么F不可能是线性变换。因为F(k0)
= a,但F(k0) ≠ kF(0)),因此线性变换不会导致平移(原点位置上不会变化)。
在某些文献中,线性变换的定义是平行线变换后仍然是平行线。大多数情况下它是对的,但有一个小小的例外:投影(当一条直线投影后变成一个点,能认为这个点平行于什么?)除了这点理论上的例外,这种定义是正确的。线性变换可能造成“拉伸”,但直线不会”弯折“,所以平行线仍然保持平行。
仿射变换
仿射变换是指线性变换后接着平移。因此仿射变换的集合是线性变换的超集,任何线性变换都是仿射变换,但不是所有仿射变换都是线性变换。
任何具有形式 v' = vM + b 的变换都是仿射变换。
可逆变换
如果存在一个逆变换可以”撤销“原变换,那么该变换是可逆的。换句话说,如果存在逆变换G,使得G(F(a))
= a,对于任意a,映射F(a)是可逆的。
存在非仿射变换的可逆变换,但暂不考虑它们。现在,我们集中精力于检测一个仿射变换是否可逆。一个仿射变换就是一个线性变换加上平移,显然,可以用相反的量”撤销“平移部分,所以问题变为一个线性变换是否可逆。
显然,除了投影以外,其他变换都能”撤销“。当物体被投影时,某一维有用的信息被抛弃了,而这些信息时不可能恢复的。因此,所有基本变换除了投影都是可逆的。
因为任意线性变换都能表达为矩阵,所以求逆变换等价于求矩阵的逆。如果矩阵是奇异的,则变换不可逆;可逆矩阵的行列式不为0。
等角变换
如果变换前后两向量夹角的大小和方向都不改变,该变换是等角的。只有平移,旋转和均匀缩放是等角变换。等角变换将会保持比例不变,镜像并不是等角变换,因为尽管两向量夹角的大小不变,但夹角的方向改变了。所有等角变换都是仿射和可逆的。
正交变换
术语“正交”用来描述具有某种性质的矩阵。正交变换的基本思想是轴保持互相垂直,而且不进行缩放变换。
平移、旋转和镜像是仅有的正交变换。长度、角度、面积和体积都保持不变。(尽管如此,但因为镜像变换被认为是正交变换,所以一定要密切注意角度、面积和体积的准确定义)。
正交矩阵的行列式为1或者负1,所有正交矩阵都是仿射和可逆的。
刚体变换
刚体变换只改变物体的位置和方向,不包括形状。所有长度、角度、面积和体积都不变。平移和旋转是仅有的刚体变换,镜像并不被认为是刚体变换。刚体变换也被称作正规变换,所有刚体变换都是正交、等角、可逆和仿射的,某些刚体变换旋转矩阵的行列式为1。