Mersenne twister -- From Wikipedia, the free encyclopedia
The Mersenne twister is a pseudorandom number generator
developed in 1997 by Makoto Matsumoto (松本 眞, Makoto Matsumoto?) and Takuji Nishimura (西村 拓士, Takuji Nishimura?)[1]
that is based on a matrix linear recurrence
over a finite binary field F2. It provides for
fast generation of very high-quality pseudorandom numbers, having been designed
specifically to rectify many of the flaws found in older algorithms.
Its name derives from the fact that period length is chosen to be a Mersenne
prime. There are at least two common variants of the algorithm, differing
only in the size of the Mersenne primes used. The newer and more commonly used
one is the Mersenne Twister MT19937, with 32-bit word length. There is also a
variant with 64-bit word length, MT19937-64, which generates a different sequence.
Application
Unlike Blum Blum Shub, the algorithm in its native form is
not suitable for cryptography. Observing a sufficient number of iterates
(624 in the case of MT19937) allows one to predict all future iterates.
Another issue is that it can take a long time to turn a non-random initial
state into output that passes randomness
tests, due to its size. A small lagged Fibonacci generator or linear congruential generator gets
started much quicker and usually is used to seed the Mersenne Twister. If only
a few numbers are required and standards aren't high it is simpler to use the
seed generator. But the Mersenne Twister will still work.
For many other applications, however, the Mersenne twister is quickly
becoming the pseudorandom number generator of choice[citation needed]. Since the
library is portable, freely available and quickly generates good quality
pseudorandom numbers it is rarely a bad choice.
It is designed with Monte Carlo simulations and other
statistical simulations in mind. Researchers primarily want good quality numbers
but also benefit from its speed and portability.
The commonly used variant of Mersenne Twister, MT19937 has the following
desirable properties:
- It was designed to have a
period of 219937 − 1 (the creators of the algorithm
proved this property). In practice, there is little reason to use larger
ones, as most applications do not require 219937 unique
combinations (219937 is approximately 4.3 × 106001).
- It has a very high order
of dimensional equidistribution (see linear congruential generator).
This implies that there is negligible serial correlation between
successive values in the output sequence.
- It passes numerous tests
for statistical randomness, including the Diehard
tests. It passes most, but not all, of the even more stringent TestU01 Crush randomness
tests.
The Mersenne Twister algorithm has received some criticism in the computer
science field, notably by George
Marsaglia. These critics claim that while it is good at generating random
numbers, it is not very elegant and is overly complex to implement. Marsaglia
has provided several examples of random number generators that are less complex
yet which he claims provide significantly larger periods. For example, a simple
complementary multiply-with-carry generator can have a period
1033000 times as long, be significantly faster, and maintain better
or equal randomness.[2][3]
Algorithmic detail
The Mersenne Twister algorithm is a twisted generalised
feedback shift register[4] (twisted GFSR, or TGFSR) of rational normal form (TGFSR(R)), with state
bit reflection and tempering. It is characterized by the following quantities:
- w: word size (in number of bits)
- n: degree of recurrence
- m: middle word, or the number of parallel sequences,
1 ≤ m ≤ n
- r: separation point of one word, or the number of
bits of the lower bitmask, 0 ≤ r ≤ w - 1
- a: coefficients of the rational normal form twist
matrix
- b, c: TGFSR(R) tempering bitmasks
- s, t: TGFSR(R) tempering bit shifts
- u, l: additional Mersenne Twister tempering
bit shifts
with the restriction that 2nw − r − 1
is a Mersenne prime. This choice simplifies the primitivity test and k-distribution
test that are needed in the parameter search.
For a word x with w bit width, it is expressed as the
recurrence relation
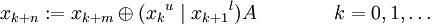
with | as the bitwise or and ⊕ as the bitwise exclusive
or (XOR), xu, xl
being x with upper and lower bitmasks applied. The twist
transformation A is defined in rational normal form
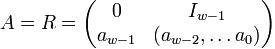
with In − 1 as the (n − 1) × (n − 1)
identity matrix (and in contrast to normal matrix multiplication, bitwise XOR
replaces addition). The rational normal form has the benefit that it can be
efficiently expressed as
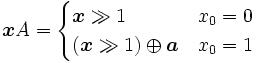
where
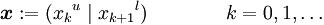
In order to achieve the 2nw − r − 1
theoretical upper limit of the period in a TGFSR, φB(t)
must be a primitive polynomial, φB(t)
being the characteristic polynomial of
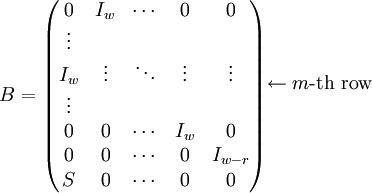
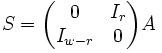
The twist transformation improves the classical GFSR with the following
key properties:
- Period reaches the
theoretical upper limit 2nw − r − 1
(except if initialized with 0)
- Equidistribution in n
dimensions (e.g. linear congruential generators
can at best manage reasonable distribution in 5 dimensions)
As like TGFSR(R), the Mersenne Twister is cascaded with a tempering transform to
compensate for the reduced dimensionality of equidistribution (because of the
choice of A being in the rational normal form), which is equivalent to
the transformation A = R → A = T−1RT,
T invertible. The tempering is defined in the case of Mersenne Twister
as
y := x ⊕ (x >> u)
y := :y ⊕ ((y << s) & b)
y := :y ⊕ ((y << t) & c)
z := y ⊕ (y >> l)
with <<, >> as the bitwise left and right shifts, and & as
the bitwise and. The first and last transforms are added in
order to improve lower bit equidistribution. From the property of TGFSR, 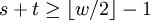 is
required to reach the upper bound of equidistribution for the upper bits.
is
required to reach the upper bound of equidistribution for the upper bits.
The coefficients for MT19937 are:
- (w, n, m,
r) = (32, 624, 397, 31)
- a = 9908B0DF16
- u = 11
- (s, b) = (7,
9D2C568016)
- (t, c) = (15,
EFC6000016)
- l = 18
Pseudocode
The following generates uniformly 32-bit integers in the range [0, 232 − 1]
with the MT19937 algorithm:
// Create a
length 624 array to store the state of the generator
int[0..623]
MT
int index =
0
// Initialize
the generator from a seed
function
initializeGenerator(int seed) {
MT[0] := seed
for i from
1 to 623 { // loop over each other element
MT[i] := last
32 bits of(1812433253 * (MT[i-1] xor (right shift by 30 bits(MT[i-1])))
+ i) // 0x6c078965
}
}
// Extract a
tempered pseudorandom number based on the index-th value,
// calling
generateNumbers() every 624 numbers
function
extractNumber() {
if
index == 0 {
generateNumbers()
}
int y
:= MT[index]
y := y xor
(right shift by 11 bits(y))
y := y xor
(left shift by 7 bits(y) and (2636928640)) // 0x9d2c5680
y := y xor
(left shift by 15 bits(y) and (4022730752)) // 0xefc60000
y := y xor
(right shift by 18 bits(y))
index :=
(index + 1) mod 624
return
y
}
// Generate an
array of 624 untempered numbers
function
generateNumbers() {
for i from
0 to 623 {
int
y := 32nd bit of(MT[i]) + last 31 bits of(MT[(i+1) mod
624])
MT[i] :=
MT[(i + 397) mod 624] xor (right shift by 1 bit(y))
if
(y mod 2) == 1 { // y is odd
MT[i]
:= MT[i] xor (2567483615) // 0x9908b0df
}
}
}
SFMT
SFMT, the SIMD-oriented
Fast Mersenne Twister, is a variant of Mersenne Twister, introduced in 2006[5], designed to be
fast when it runs on 128-bit SIMD.
- It is roughly twice as
fast as Mersenne Twister.[6]
- It has a better equidistribution property of v-bit accuracy
than MT but worse than WELL ("Well Equidistributed Long-period
Linear").
- It has quicker recovery
from zero-excess initial state than MT, but slower than WELL.
- It supports various
periods from 2607-1 to 2216091-1.
Intel SSE2 and PowerPC AltiVec
are supported by SFMT. It is also used for games with the Cell BE in the Playstation
3.[7]
References
- ^ M. Matsumoto & T.
Nishimura, "Mersenne twister: a 623-dimensionally equidistributed
uniform pseudorandom number generator", ACM Trans. Model. Comput.
Simul. 8, 3 (1998).
- ^ Marsaglia
on Mersenne Twister 2003
- ^ Marsaglia
on Mersenne Twister 2005
- ^ M. Matsumoto & Y.
Kurita, "Twisted GFSR generators", ACM Trans. Model. Comput.
Simul. 2, 179 (1992); 4, 254 (1994).
- ^ SIMD-oriented
Fast Mersenne Twister (SFMT)
- ^ SFMT:Comparison
of speed
- ^ PLAYSTATION 3 License
External links
Implementations
这里有这种算法三个版本的C/C++实现代码:http://www.cppblog.com/Files/Chipset/random.zip