Stride is an important concept in digital image processing. It allows performing several operations with an image in a very fast manner (in constant time) by simple modification of image metadata. If you are interested in finding out what stride is and how to use it stick with us.
Pixel representation in a computer memory
Before we dive into the concept of stride we first need to revise how digital images are stored in a computer memory. We will start from a pixel.
An image pixel is represented in a computer memory by a fixed number of bits. Typical pixel bit depth (amount of bits per pixel) is 32, 16, 8 or, for binary images, 1 bit. In typical RGB images, 8 bits are often used to store the color value of a single channel. Thus, the total bit depth of one pixel is 24. Processing 32 and 16-bit chunks of data is simple and effective on a typical 32 and 64-bit processors. Therefore, the pixels are stored in the format of 32 bits, where the older (or younger, depending on the implementation) 8 bits remain unused. Such an approach to storing pixels requires more memory, but it allows speeding up image processing by using the standard size of the machine word. Thus, a standard RGB image occupies 32 bits in memory and has a depth of 24 bits. We will call another 8 bits necessary to supplement the size of the memory occupied by a pixel to the value of a multiple of degree 2, pixel padding. The total number of bytes occupied by a pixel in memory is called pixel stride (See Image 1).
Image representation in a computer memory
Images are stored in computer memory pixel-by-pixel, line by line. The upper left corner of the image is usually chosen as a coordinate origin (the upper left pixel of the image has the index [0, 0]). The image is stored in memory as a one-dimensional array. Pixels of the first line of the image are first written to the memory, then pixels of the second line and so on up to the last line. Each line in addition to the pixel bytes may also contain additional bytes — line padding. Additional bytes usually do not contain useful information and do not affect the visualization of an image when, for example, displayed on the screen. These additional bytes serve to complement a line, which is necessary for more efficient image processing and is caused by the specificity of the hardware used. For example, Cairo (a popular open source vector graphics software library) requires alignment of rows to multiple 4 bytes, which allows for more efficient image processing algorithms using vectorized processor operations and processing several image pixels simultaneously.
Introducing the term of line padding requires to introduce another closely coupled term — line stride.
Line stride (increment, pitch or step size) is the number of bytes that one needs to add to the address in the first pixel of a row in order to go to the address of the first pixel of the next row. It is important to note that an image width is measured in pixels and describes an image itself (and doesn’t depend on how an image is stored in a computer memory). In contrast, a line stride depends on how an image is represented in memory and is measured in bytes.
In program source code, an image is usually represented by a data structure containing metadata (image width and height, line stride, number of channels, encoding type, etc.), as well as a pointer to the address of the first image pixel in memory (further we will refer to this address as data_begin). This information allows us to unambiguously read and decode an image from memory, as well as to perform a series of fast image operations by changing only a metadata associated with an image.
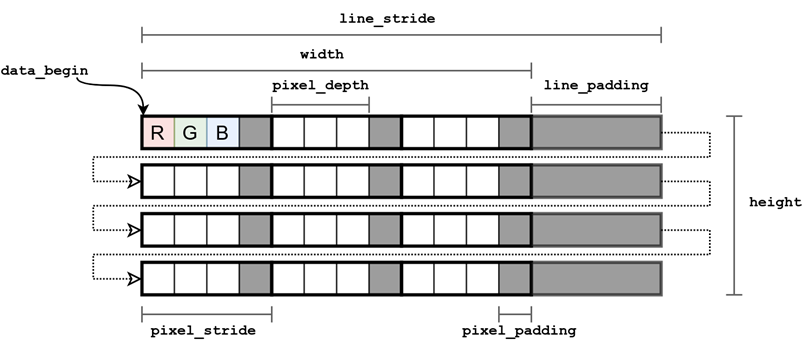
An image representation in a computer memory. Lines of an image are stored one by one in one-dimensional array.
Image operations:
Let’s summarize all the terms which we introduced to this moment:
pixel_address — a pixel address in memory
pixel depth —the number of bits per pixel (containing valuable information)
pixel_stride — the number of bytes occupied in memory by a pixel of an image
data_begin — the address of the first image pixel in memory
channels — the number of image channels (3 for an RGB-image)
channel_address — the address of a particular pixel channel in memory
height — the image height in pixels
width — the image width in pixels
line_stride — the number of bytes occupied in memory by a line of an image
Operations:
1. Computing pixel address in memory
The equation relating pixel memory address to its coordinates [y, x] in the image coordinate system can be represented as:
pixel_address = data_begin + y * line_stride + x * pixel_stride, (1)
where data_begin — the address of the first image pixel in memory.
Equation (1) is used whenever you access an image in memory. In the rest of operations, presented in this post, we will only change a metadata associated with an image and assume, that the equation (1) is applied after in order to access image.
2. Pixel decoding (for RGB image with an equal amount of bits per channel):
channel_address = pixel_address + n * depth / channels, (2)
where n is a channel index: n = 0, 1, …, channels — 1. Thus, for instance, for the typical RGB-image with an equal amount of bits per channel, a channel address in memory can be computed as follows:
R = pixel_address,
G = pixel_address + depth / channels,
B = pixel_address + 2 * depth / channels.
It is important to note that these equations depend on the type of the image stored. There are formats in which different number of bytes is used to store different channels.
3. Image flip
3.1 Vertical flip
data_begin = data_begin + (height- 1) * line_stride ,
line_stride = -line_stride.
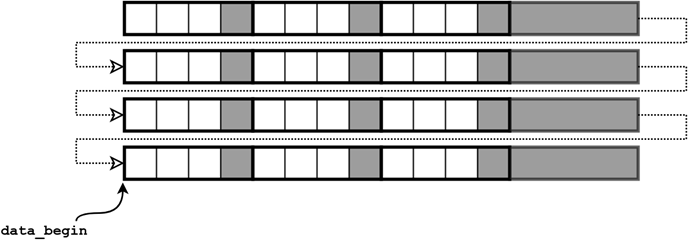
Pointer to the first image pixel for the vertical flip
The negative line stride being inserted into equation (1) allows us to move upwards reading (or visualizing) an image from the last row to the first, thus, realizing vertical flip.
3.2 Horizontal flip
data_begin = data_begin + (width — 1) * pixel_stride ,
pixel_stride = -pixel_stride.
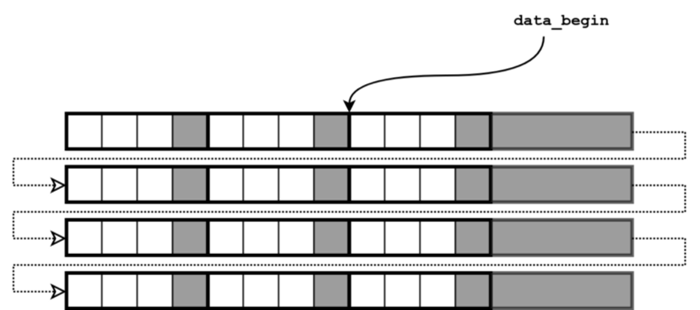
Pointer to the first image pixel for the horizontal flip
In the same manner as with negative line stride in the previous example, the negative pixel stride here allows us to move from right to left and to read (or visualize) an image flipped horizontally.
3.3 Vertical and horizontal flip
The combination of previous two approaches allows to flip an image in both directions at once:
data_begin = data_begin + (height-1) * line_stride + (width-1) * pixel_stride,
line_stride = -line_stride,
pixel_stride = -pixel_stride.
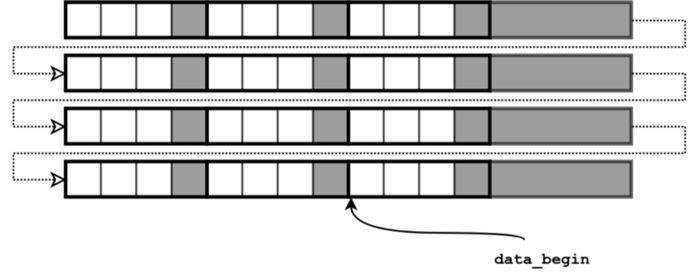
Pointer to the first image pixel for the simultaneous vertical and horizontal flip
4. Extracting image subwindow
data_begin = new_data_begin,
width = new_width,
height = new_height.
With this approach we set a new origin of our image (inside a boundary of the original image) and set a width and height which basically tell us how many time we should apply an equation (1) to read all pixels (width x height) and after which amount of pixels read we should increase the y coordinate (to start reading pixels of the next row). Note that such parameters as line stride remain unchanged.
5. Extracting single image channel
To extract a single image channel we can use a combination of equations (1) and (2):
pixel_address = data_begin + y * line_stride + x * pixel_stride + n * depth / channels,
where n — channel index, n = 0, 1, …, channels — 1.
REFERENCES
1. A programmer’s view on digital images: the essentials: https://www.collabora.com/news-and-blog/blog/2016/02/16/a-programmers-view-on-digital-images-the-essentials/
2. Microsoft Media Foundation Programming Guide: Image Stride:Image Stride When a video image is stored in memory, the memory buffer might contain extra padding bytes after each row of pixels…docs.microsoft.com
3. Wikipedia: Stride of an array: https://en.wikipedia.org/wiki/Stride_of_an_array
4. Cairo library: https://cairographics.org/