Bernoulli Equation

The Bernoulli Equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. The qualitative behavior that is usually labeled with the term "Bernoulli effect" is the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy.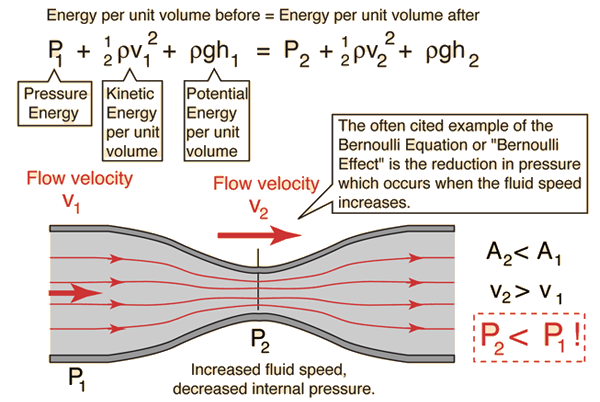

Steady-state flow caveat: While the Bernoulli equation is stated in terms of universally valid ideas like conservation of energy and the ideas of pressure, kinetic energy and potential energy, its application in the above form is limited to cases of steady flow. For flow through a tube, such flow can be visualized as laminar flow, which is still an idealization, but if the flow is to a good approximation laminar, then the kinetic energy of flow at any point of the fluid can be modeled and calculated. The kinetic energy per unit volume term in the equation is the one which requires strict constraints for the Bernoulli equation to apply - it basically is the assumption that all the kinetic energy of the fluid is contributing directly to the forward flow process of the fluid. That should make it evident that the existence of turbulence or any chaotic fluid motion would involve some kinetic energy which is not contributing to the advancement of the fluid through the tube.

It should also be said that while conservation of energy always applies, this form of parsing out that energy certainly does not describe how that energy is distributed under transient conditions. A good visualization of the Bernoulli effect is the flow through a constriction, but that neat picture does not describe the fluid when you first turn on the flow.

Another approximation involved in the statement of the Bernoulli equation above is the neglect of losses from fluid friction. Idealized laminar flow through a pipe can be modeled by Poiseuille's law, which does include viscous losses resulting in a lowering of the pressure as you progress along the pipe. The statement of the Bernoulli equation above would lead to the expectation that the pressure would return to the value P₁ past the constriction since the radius returns to its original value. This is not the case because of the loss of some energy from the active flow process by friction into disordered molecular motion (thermal energy). More accurate modeling can be done by combining the Bernoulli equation with Poiseuille's law. A real example which might help visualize the process is the pressure monitoring of the flow through a constricted tube.

Bernoulli Calculation

Curve of a Baseball

A non-spinning baseball or a stationary baseball in an airstream exhibits symmetric flow. A baseball which is thrown with spin will curve because one side of the ball will experience a reduced pressure. This is commonly interpreted as an application of the Bernoulli principle and involves the viscosity of the air and the boundary layer of air at the surface of the ball.

The roughness of the ball's surface and the laces on the ball are important! With a perfectly smooth ball you would not get enough interaction with the air.

There are some difficulties with this picture of the curving baseball. The Bernoulli equation cannot really be used to predict the amount of curve of the ball; the flow of the air is compressible, and you can't track the density changes to quantify the change in effective pressure. The experimental work of Watts and Ferrer with baseballs in a wind tunnel suggests another model which gives prominent attention to the spinning boundary layer of air around the baseball. On the side of the ball where the boundary layer is moving in the same direction as the free stream air speed, the boundary layer carries further around the ball before it separates into turbulent flow. On the side where the boundary layer is opposed by the free stream flow, it tends to separate prematurely. This gives a net deflection of the airstream in one direction behind the ball, and therefore a Newton's 3rd law reaction force on the ball in the opposite direction. This gives an effective force in the same direction indicated above.

Similar issues arise in the treatment of a spinning cylinder in an airstream, which has been shown to experience lift. This is the subject of the Kutta-Joukowski theorem. It is also invoked in the discussion of airfoil lift.

Airfoil

The air across the top of a conventional airfoil experiences constricted flow lines and increased air speed relative to the wing. This causes a decrease in pressure on the top according to the Bernoulli equation and provides a lift force. Aerodynamicists (see Eastlake) use the Bernoulli model to correlate with pressure measurements made in wind tunnels, and assert that when pressure measurements are made at multiple locations around the airfoil and summed, they do agree reasonably with the observed lift.

Illustration of lift force and angle of attack Bernoulli vs Newton for airfoil lift Airfoil terminology

Others appeal to a model based on Newton's laws and assert that the main lift comes as a result of the angle of attack. Part of the Newton's law model of part of the lift force involves attachment of the boundary layer of air on the top of the wing with a resulting downwash of air behind the wing. If the wing gives the air a downward force, then by Newton's third law, the wing experiences a force in the opposite direction - a lift. While the "Bernoulli vs Newton" debate continues, Eastlake's position is that they are really equivalent, just different approaches to the same physical phenonenon. NASA has a nice aerodynamics site at which these issues are discussed. Increasing the angle of attack gives a larger lift from the upward component of pressure on the bottom of the wing. The lift force can be considered to be a Newton's 3rd law reaction force to the force exerted downward on the air by the wing. At too high an angle of attack, turbulent flow increases the drag dramatically and will stall the aircraft.

A vapor trail over the wing helps visualize the air flow. Photo by Frank Starmer, used by permission.