四、从正则表达式到ε-NFA

通过第二节所描述的内容，我们知道一个正则表达式的基本元素就是字符集。通过对规则的串联、并联、重复、可选等操作，我们可以构造除更复杂的正则表达式。如果从正则表达式构造状态机的时候也可以用这几种操作对状态图进行组合的话，那么方法将会变得很简单。接下来我们将一一对这5个构造正则表达式的方法进行讨论。使用下文描述的算法构造出来的所有ε-NFA都有且只有一个结束状态。

1：字符集

字符集是正则表达式最基本的元素，因此反映到状态图上，字符集也会是构成状态图的基本元素。对于字符集C，如果有一个规则只接受C的话，这个规则对应的状态图将会被构造成以下形式：

 

 

图4.1

这个状态图的初始状态是Start，结束状态是End。Start状态读入字符集C跳转到End状态，不接受其他字符集。

2：串联

如果我们使用A⊙B表示规则A和规则B的串联，我们可以很容易的知道串联这个操作具有结合性，也就是说(A⊙B)⊙C=A⊙(B⊙C)。因此对于n个规则的串联，我们只需要先将前n-1个规则进行串连，然后把得到的规则看成一个整体，跟最后一个规则进行串联，那么就得到了所有规则的串联。如果我们知道如何将两个规则串联起来的话，也就等于知道了如何把n个规则进行串联。

为了将两个串联的规则转换成一个状态图，我们只需要先将这两个规则转换成状态图，然后让第一个状态的结束状态跳转到第二个状态图的起始状态。这种跳转必须是不读入字符的跳转，也就是令这两个状态等价。因此，第一个状态图跳转到了结束状态的时候，就可以当成第二个状态图的起始状态，继续第二个规则的检查。因此我们使用了ε边连接两个状态图：

 

 

图4.2

3：并联

并联的方法跟串联类似。为了可以在起始状态读入一个字符的时候就知道这个字符可能走的是并联的哪一些分支并进行跳转，我们需要先把所有分支的状态图构造出来，然后把起始状态连接到所有分支的起始状态上。而且，在某个分支成功接受了一段字符串之后，为了让那个状态图的结束状态反映在整个状态图的结束状态上，我们也把所有分支的结束状态都连接到大规则的结束状态上。如下所示：

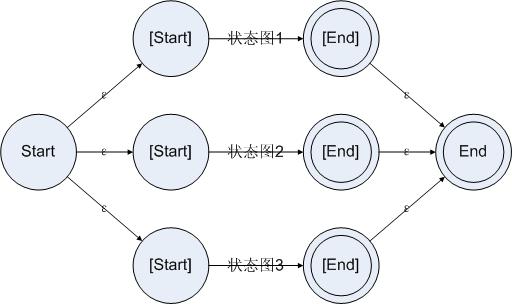
图4.3

4：重复

对于一个重复，我们可以设立两个状态。第一个状态是起始状态，第二个状态是结束状态。当状态走到结束状态的时候，如果遇到一个可以让规则接受的字符串，则再次回到结束状态。这样的话就可以用一个状态图来表示重复了。于是对于重复，我们可以构造状态图如下所示：

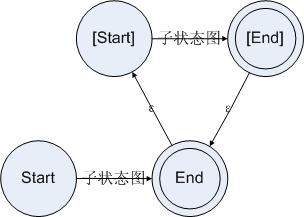
图4.4

5：可选

为可选操作建立状态图比较简单。为了完成可选操作，我们需要在接受一个字符的时候，如果字符串的前缀被当前规则接受则走当前规则的状态图，如果可选规则的后续规则接受了字符串则走后续规则的状态图，如果都接受的话就两个图都要走。为了达到这个目的，我们把规则的状态图的起始状态和结束状态连接起来，得到了如下状态图：

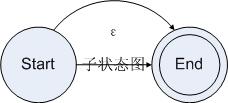
图4.5

如果重复使用的是0次以上重复，也就是原来的重复加上可选的结果，那么可以简单地把图4.4的Start状态去掉，让End状态同时拥有起始状态和结束状态两个角色，[Start]和[End]则保持原状。

至此，我们已经将5种构造状态图的办法都对应到了5种构造规则的办法上了。对于任意的一个正则表达式，我们仅需要把这个表达式还原成那5种构造的嵌套，然后把每一步构造都对应到一个状态图的构造上，就可以将一个正则表达式转换成一个ε-NFA了。举个例子，我们使用正则表达式来表达“一个字符串仅包含偶数个a和偶数个b”，然后把它转换成ε-NFA。

我们先对这个问题进行分析。如果一个字符串仅包含偶数个a和偶数个b的话，那么这个字符串一定是偶数长度的。于是我们可以把这个字符串分割成两个两个的字符段。而且这些字符段只有四种：aa、bb、ab和ba。对于aa和bb来说，无论出现多少次都不会影响字符串中a和b的数量的奇偶性(理由：在一个模2加法系统里，0是不变项，也就是说对于任何属于模2加法的数X有X+0 = 0+X = X)。对于ab和ba的话，如果一个字符串的开始和结束是ab或者ba，中间的部分是aa或者bb的任意组合，这个字符串也是具有偶数个a和偶数个b的。我们现在得到了两种构造偶数个a和偶数个b的字符串的方法。把串联、并联、可选、重复等操作应用在这些字符串上，仍然会得到具有偶数个a和偶数个b的字符串。于是我们可以把正则表达式书写成以下形式：

((aa|bb)|((ab|ba)(aa|bb)*(ab|ba)))*

根据上文提到的方法，我们可以把这个正则表达式转换成以下状态机：

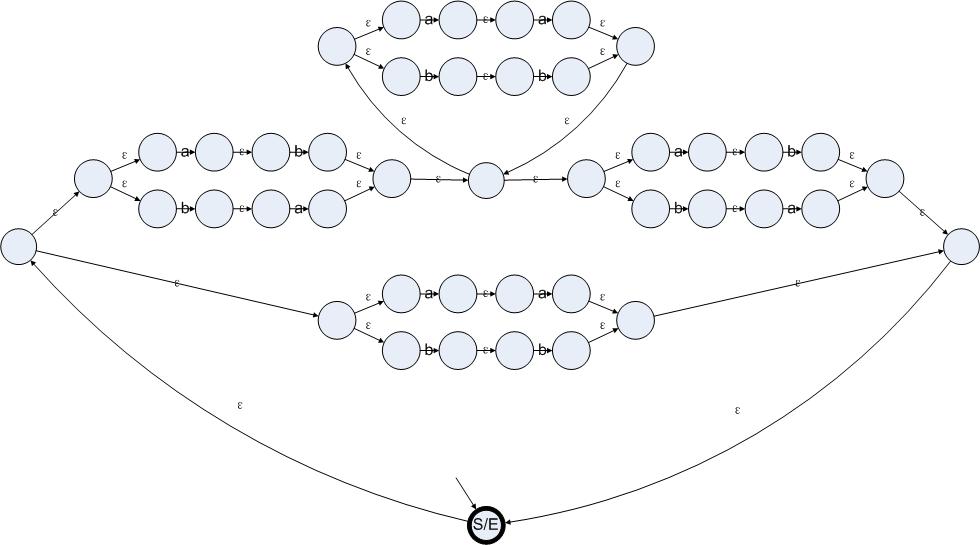
图4.6

至此，我们已经得到了把一个正则表达式转换为ε-NFA的方法了。但是只得到ε-NFA还是不行的，因为ε-NFA的不确定性太大了，直接根据ε-NFA跑的话，每一次都会得到大量的临时状态集合，会极大地降低效率。因此，我们还需要一个办法消除一个状态机的非确定性。