In statistics, an expectation-maximization (EM) algorithm is a method for finding maximum likelihood ormaximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. EM is an iterative method which alternates between performing an expectation (E) step, which computes the expectation of the log-likelihood evaluated using the current estimate for the latent variables, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.
EM算法可用于很多问题的框架，其中需要估计一组描述概率分布的参数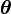
，只给定了由此产生的全部数据中能观察到的一部分！
EM算法是一种迭代算法，它由基本的两个步骤组成：
E step：估计期望步骤
使用对隐变量的现有估计来计算log极大似然
M step: 最大化期望步骤
计算一个对隐变量更好的估计，使其最大化log似然函数对隐变量Y的期望。用新计算的隐变量参数代替之前的对隐变量的估计，进行下一步的迭代！
观测数据：观测到的随机变量X的IID样本：
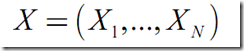
缺失数据：未观测到的隐含变量(隐变量)Y的值：
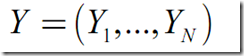
完整数据： 包含观测到的随机变量X和未观测到的随机变量Y的数据，Z=(X,Y)
似然函数：(似然函数的几种写法)
D_HBNI489~H%7DGCRMWVJ_thumb.jpg "JL})D_HBNI489~H}GCRMWVJ")
log似然函数为：
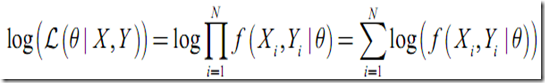
E step：用对隐变量的现有估计
计算隐变量Y的期望
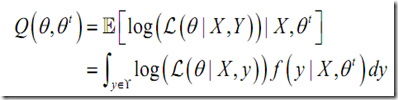
其中需要用到贝叶斯公式：
M step：最大化期望，获得对隐变量更好的估计
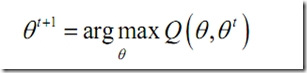
维基中的表述是这样子：
Given a statistical model consisting of a set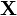 
of observed data, a set of unobserved latent data or missing values Y, and a vector of unknown parameters 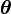, along with a likelihood function 
, the maximum likelihood estimate (MLE) of the unknown parameters is determined by the marginal likelihood of the observed data
)%25ZR_thumb.jpg "CR%M2I[QD88[N5$3(H))%ZR")
However, this quantity is often intractable.
The EM algorithm seeks to find the MLE of the marginal likelihood by iteratively applying the following two steps:
- Expectation step (E-step): Calculate the expected value of the log likelihood function, with respect to the conditional distribution of Y given 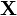under the current estimate of the parameters :
![A7DFNWMY)KAI]T5)_OMKRUD](http://www.cppblog.com/images/cppblog_com/sosi/WindowsLiveWriter/Expectationmaximizationalgorithm_C294/A7DFNWMY)KAI%5DT5)_OMKRUD_thumb.jpg "A7DFNWMY)KAI]T5)_OMKRUD")
- Maximization step (M-step): Find the parameter that maximizes this quantity:
Note that in typical models to which EM is applied:
- The observed data points 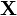may be discrete (taking one of a fixed number of values, or taking values that must be integers) or continuous (taking a continuous range of real numbers, possibly infinite). There may in fact be a vector of observations associated with each data point.
- The missing values (aka latent variables) Y are discrete, drawn from a fixed number of values, and there is one latent variable per observed data point.
- The parameters are continuous, and are of two kinds: Parameters that are associated with all data points, and parameters associated with a particular value of a latent variable (i.e. associated with all data points whose corresponding latent variable has a particular value).
However, it is possible to apply EM to other sorts of models.
The motivation is as follows. If we know the value of the parameters 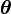, we can usually find the value of the latent variables Y by maximizing the log-likelihood over all possible values of Y, either simply by iterating over Y or through an algorithm such as the Viterbi algorithm for hidden Markov models. Conversely, if we know the value of the latent variables Y, we can find an estimate of the parameters 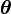fairly easily, typically by simply grouping the observed data points according to the value of the associated latent variable and averaging the values, or some function of the values, of the points in each group. This suggests an iterative algorithm, in the case where both 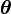and Y are unknown:
- First, initialize the parameters 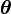to some random values.
- Compute the best value for Y given these parameter values.
- Then, use the just-computed values of Y to compute a better estimate for the parameters 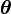. Parameters associated with a particular value of Y will use only those data points whose associated latent variable has that value.
- Finally, iterate until convergence.
The algorithm as just described will in fact work, and is commonly called hard EM. The K-means algorithm is an example of this class of algorithms.
However, we can do somewhat better by, rather than making a hard choice for Y given the current parameter values and averaging only over the set of data points associated with a particular value of Y, instead determining the probability of each possible value of Y for each data point, and then using the probabilities associated with a particular value of Y to compute a weighted average over the entire set of data points. The resulting algorithm is commonly called soft EM, and is the type of algorithm normally associated with EM. The counts used to compute these weighted averages are called soft counts (as opposed to the hard counts used in a hard-EM-type algorithm such as K-means). The probabilities computed for Y areposterior probabilities and are what is computed in the E-step. The soft counts used to compute new parameter values are what is computed in the M-step.
总结：
EM is frequently used for data clustering in machine learning and computer vision.
EM会收敛到局部极致，但不能保证收敛到全局最优。
EM对初值比较敏感，通常需要一个好的，快速的初始化过程。
这是我的Machine Learning课程，先总结到这里， 下面的工作是做一个GM_EM的总结，多维高斯密度估计！