是技术，更是艺术

     摘要: cout遇到的这个小问题，主要有两点值得注意：其一，参数入栈的顺序在c++默认调用约定下是从右向左的；其二，第一趟将每个参数计算出当前参数表达式的值。另外，当我们发现有些问题不好理解时候，最好的方法就是查看反汇编代码。  阅读全文

 

如果要返回环的入口节点
一种效率比较低的方法是
一个指针p1从表头开始，指针p2 初始化为判环时找到的指针，p1每前进一步，由p2遍历一次环中各结点，遍历过程中每次都要判断p1是否p2
当p2 == fast时候，p1 = p1.next，继续循环。这样肯定能找到入口，但是效率为O(n^2)

这个问题源于《编程之美》2.14 求数组的子数组之和的最大值扩展问题2

输出子数组的最大和同时输出子数组下标，时间复杂度为O(N)
源码：

    引理：如果 a 是一个大于1的整数，而所有小于或等于根号 a  的素数都除不尽 a ，则 a 是素数。
理想的判断素数的方法应该是将所有小于或等于根号n的素数去除n，但是n是一个随机大于1的整数，小于这个数的平方根的素数表不好给定。下面介绍的方法，本意是动态的构建素数表，但是引入了很多冗余的除数。

代码：

分析：
　　相对于sqrt(n)次除，上面的程序需要sqrt(n)*8/30次除，效率提升了15/4倍。
　　自然数n，我们假设小于n的素数数F(n),F(n)的分布规律为：当n趋向于无穷大时，F(n)/(x/logx) = 1;
        所以，动态的冗余度近似为：(sqrt(n)*4/15-x/logx)/sqrt(n)*4/15

其他更好的判断素数的算法，希望你能给我留言或者写在评论上，谢谢！

    申明：Blog上的文章只是个人学习的一些记录和总结，这些记录部分来自于网络，加上自己的一些理解，有些已经找不到最原始的出处了，在此对大牛们的贡献表示感谢，如有侵权的地方，请通知我，我会尽快删除。
         对关注性能的程序开发人员而言，一个好的计时部件既是益友，也是良师。计时器既可以作为程序组件帮助程序员精确的控制程序进程，又是一件有力的调试武器，在有经验的程序员手里可以尽快的确定程序的性能瓶颈，或者对不同的算法作出有说服力的性能比较。GPU程序性能瓶颈测试，比较常用的工具是NVIDIA PerfHUD ，它能准确测量出渲染管线的每个阶段消耗的时间，从时间轴上可以很明显的看出在渲染一帧是，渲染瓶颈在哪个阶段，从而根据具体情况进行优化。CPU程序性能分析工具，Intel公司的 VTune在业界比较常用，一直想用，还没试过。
         然而下面将要介绍的，从网上搜集到的一些关于程序代码段时间统计函数，用于单个算法的性能分析，比上面提及的工具，更加方便，轻量，易用，根据你对时间统计的精度要求，选择不同的时间统计函数。
1.C语言时间库<time.h>的clock()函数
2. RDTSC :(Read Time Stamp Counter) _[1]
在Intel   Pentium以上级别的CPU中，有一个称为“时间戳（Time   Stamp）”的部件，它以64位无符号整型数的格式，记录了自CPU上电以来所经过的时钟周期数。由于目前的CPU主频都非常高(1GHz = 10⁹⁾，因此这个部件可以达到纳秒级(一秒的10亿分之一，即等于10的负9次方秒)的计时精度。这个精确性是上述方法所无法比拟的。在Pentium以上的CPU中，提供了一条机器指令RDTSC（Read   Time   Stamp   Counter）来读取这个时间戳的数字，并将其保存在EDX:EAX寄存器对中。由于EDX:EAX寄存器对恰好是Win32平台下C++语言保存函数返回值的寄存器，所以我们可以把这条指令，嵌入汇编代码的方式，看成是一个普通的函数调用。像这样：   
但是不行，因为RDTSC不被C++的内嵌汇编器直接支持，所以我们要用_emit伪指令直接嵌入该指令的机器码形式0X0F、0X31，如下：   
   以后在需要计数器的场合，可以调用两次GetCycleCount函数，比较两个返回值的差，像这样：   
我的CPU是2.0GHz
所以输出结果：
时间：1995027270
程序所花时间秒数   =   RDTSC读出的周期数T1-RDTSC读出周期数T2   /   CPU主频速率（Hz）
缺点：
    1.数据抖动比较厉害，每次测得结果都不一样，波动幅度上百甚至上千
    2.在多核下不准确或不可用，有以下几个方面的原因_[2]：
       a.两个CPU核的内部计数器不同步。如果程序两次读取这个计数器的时候恰好被轮换到不同的核上，那么用来计时就会有比较大的误差。
       b.CPU 的时钟频率可能变化，例如笔记本电脑的节能功能；
       c.乱序执行导致 RDTSC 测得的周期数不准，这个问题从 Pentium Pro 时代就存在。
解决方法_[3]：可以采用设定线程亲核性的方法。函数SetThreadAffinityMask可以指定某线程只在某些核上运行（由第二个参数设定，每个位代表一个核）。例如，在需要调用RDTSC的那个线程里执行SetThreadAffinityMask(GetCurrentThread(), 0x00000001);就能保证该线程只在第一个核上运行，不会因为两个核的RDTSC计数器不同步而造成计时误差。我在windows7和VS2005下测试，测出的数据和我CPU主频不符，我一度怀疑刚买的笔记本是不是被刷屏了，后来还找了其他的一些测CPU的工具，比如CPU-Z，这个问题还没解决。
3.使用QueryPerformanceCounter查询函数方法
这个方法在多核下照常有效，QueryPerformanceFrequency()参数只和主板上的高精度定时器的晶振频率相关
在面的例子是两种求平方根的算法的性能比较，一种采用库函数的sqrt(),另一种方法是《编程珠玑》上介绍的牛顿迭代法求平方根，原理类似于二分查找，但是牛顿迭代法收敛速度相比快很多。

两种求平方根所需时间对比如下：

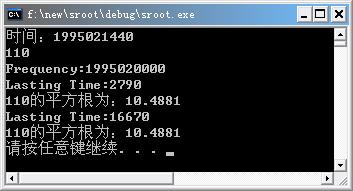
在图形学中求平方根使用频率非常高，尤其是在碰触检测中，尽量提高求平方根的效率是非常有必要的。
总结：效率就是生命，在平时的项目开发中尽量做到简单，简单代表高效。这是检测高效的第一步。
引用：
[1]:http://zhidao.baidu.com/question/41853032.html
[2]:http://blog.csdn.net/Solstice/archive/2010/01/16/5196544.aspx
[3]:http://blog.21ic.com/user1/5184/archives/2009/65439.html

《more effective c++》条款19：
c++真正的所谓临时对象是不可见的----不会在你的源代码出现。

无名临时对象通常发生在两种情况：
1. 当隐式类型转换(implicit type conversions)发生时；
2. 当函数返回对象时。

了解这些临时对象如何被产生和被销毁，很重要，因为这些对象伴随的构造成本和析构成本可能对你的程序性能产生值得注意的冲击。

     摘要: 之前遇到QT不支持TGA图片显示的缺陷，人家写的一种弥补的办法，借用一下，手动写一个函数，加载TGA图片，希望对遇到同样问题的朋友有用。如果你有更好的方法也不妨告诉我，非常感谢！   1#define QT3_SUPPORT   2#include <QtGui/QApplication.h>  ...  阅读全文

我们现在想做的是类似Unreal 3中材质编辑器
设计思想就是，美工可以很容易的实现想要实现的材质，而不需要动手编码，只需要拉你需要的表示进行组织，通过带箭头的线连接起来，what you see is what you play：基本框架已经出来，能实现少量几种材质效果，比如：法线，视差，Relief

我希望结识一些研究实时渲染的朋友，一起交流GPU编程！！！

贴几张效果图：

1.没有添加任何特效的贴图：


2.加上法线贴图的贴图：


3.加一张黑白图做偏移参照，视差偏移贴图：

1 string转CString

CString.format("%s",string.c_str());

2 CString 转 string

UNICODE编码：
CString inStr;
setlocale(LC_ALL,"chs");
char* p = new char[...];//足够长
wcstombs( p , str , str.GetLength() );
string outStr = p; 
ASCII编码：
CString inStr;
string outStr = (const char*)str;

3 Char* 转CString

CSstring.format("%s",char*);

4 CString互转char*   

CString strtest;  
char * charpoint;  
charpoint=strtest.GetBuffer(strtest.GetLength());  

5 char *转 string 

string s(char*);

6 string 转 char * 

char *p = string.c_str();  

《C++标准函数库》中说的  
有三个函数可以将字符串的内容转换为字符数组和C—string  
1.data(),返回没有”\0“的字符串数组  
2,c_str()，返回有”\0“的字符串数组  
3，copy()  

7 CString转int 

CString ss="1212.12";  
int temp=atoi(ss); 

//CString aaa = "16" ; 
//int int_chage = atoi((lpcstr)aaa) ; 

8 int转CString

CString aa;  
aa.Format("%d",temp); 
Format函数的功能很强，好好研究一下。

9 int 转 string

int a = 2;
char p[NUM];//NUM够用
string desStr = itoa(a,p,10)//第三个参数很有意思，这里的10代表的是10进制，如果你的例子中 a =10 ,itoa(a,p,16)的话，desStr = "a";

10 string 转 int

string srcStr= "222";
int a = atoi(srcStr);