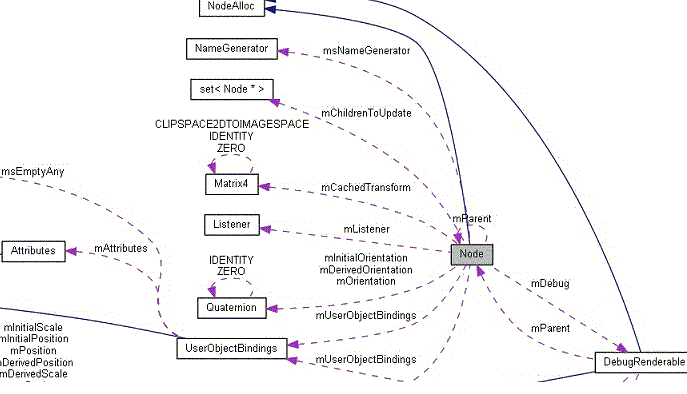
第一天，神说要有math，要计算法线，于是就有了Ogre::math，有了法线计算。
/**//** Calculate a face normal, including the w component which is the offset from the origin. */
static Vector4 calculateFaceNormal(const Vector3& v1, const Vector3& v2, const Vector3& v3);
/**//** Calculate a face normal, no w-information. */
static Vector3 calculateBasicFaceNormal(const Vector3& v1, const Vector3& v2, const Vector3& v3);
/**//** Calculate a face normal without normalize, including the w component which is the offset from the origin. */
static Vector4 calculateFaceNormalWithoutNormalize(const Vector3& v1, const Vector3& v2, const Vector3& v3);
/**//** Calculate a face normal without normalize, no w-information. */
static Vector3 calculateBasicFaceNormalWithoutNormalize(const Vector3& v1, const Vector3& v2, const Vector3& v3);
文如其名，四个上帝之子是同胞胎，只为了一个目的：得到法线，和一个附加长度。
//-----------------------------------------------------------------------
Vector4 Math::calculateFaceNormal(const Vector3& v1, const Vector3& v2, const Vector3& v3)
{
Vector3 normal = calculateBasicFaceNormal(v1, v2, v3);
// Now set up the w (distance of tri from origin
return Vector4(normal.x, normal.y, normal.z, -(normal.dotProduct(v1)));
}
//-----------------------------------------------------------------------
Vector3 Math::calculateBasicFaceNormal(const Vector3& v1, const Vector3& v2, const Vector3& v3)
{
Vector3 normal = (v2 - v1).crossProduct(v3 - v1);
normal.normalise();
return normal;
}
//-----------------------------------------------------------------------
Vector4 Math::calculateFaceNormalWithoutNormalize(const Vector3& v1, const Vector3& v2, const Vector3& v3)
{
Vector3 normal = calculateBasicFaceNormalWithoutNormalize(v1, v2, v3);
// Now set up the w (distance of tri from origin)
return Vector4(normal.x, normal.y, normal.z, -(normal.dotProduct(v1)));
}
//-----------------------------------------------------------------------
Vector3 Math::calculateBasicFaceNormalWithoutNormalize(const Vector3& v1, const Vector3& v2, const Vector3& v3)
{
Vector3 normal = (v2 - v1).crossProduct(v3 - v1);
return normal;
}
上帝是多么的英明，在你千辛万苦google后却还是无果的时候，却发现圣书上古老的笔迹是最好的诠释。
第二天，上帝走在水面上，说要有一个面，于是就有了平面。
Ogre::MeshManager::getSingleton().createPlane("floor", Ogre::ResourceGroupManager::DEFAULT_RESOURCE_GROUP_NAME,
Plane(Vector3::UNIT_Y, 0), 200, 200, 10, 10, true, 1, 10, 10, Vector3::UNIT_Z);
// create a floor entity, give it a material, and place it at the origin
Ogre::Entity* floor = mSceneMgr->createEntity("Floor", "floor");
floor->setMaterialName("Examples/Rockwall");
floor->setCastShadows(false);
mSceneMgr->getRootSceneNode()->attachObject(floor);第三天，神说要有点、也要有叉。点点叉叉才像世界。
1).点积
维基：
http://en.wikipedia.org/wiki/Dot_product
点积没有其他的几何意义，除了表示2个向量的角度：
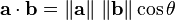
同时在ogre代码中:
inline Real Vector3::dotProduct(const Vector3& vec) const
{
return x * vec.x + y * vec.y + z * vec.z;
}
这里也可以看到一个互动效果的点积图形程序：
http://xahlee.org/SpecialPlaneCurves_dir/ggb/Vector_Dot_Product.html
也可以看到在其他领域点积还是有意义的，例如物理
2).叉积
维基：
http://en.wikipedia.org/wiki/Cross_product
叉积的结果正好是面的法线向量。这个向量的绝对值正好是向量包围体的体积\面积。
叉积的结果表示：
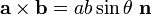
同时在ogre代码中:
inline Vector3::Vector3 crossProduct( const Vector3& rkVector ) const
{
return Vector3(
y * rkVector.z - z * rkVector.y,
z * rkVector.x - x * rkVector.z,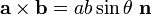
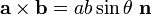
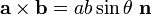x * rkVector.y - y * rkVector.x);
}
3).四元数
一个四元数可以对应一个4*4矩阵，这是上帝的法则，作为它的子民，只有依其言行事。
这里你可以看到四元数---对应矩阵---模型的互动操作，I love It！当然，只板樯才可以让演示程序跑起来，I 罚克中国恭馋裤裆。
http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToMatrix/program/index.htm
这个站还有四元数相关运算的详细推导，例如四元数转4*4矩阵。
4).矩阵
第四天，上帝想考验世人的信仰，想看看每一颗心是不是红的。
Entity *ent = NULL;
// mesh data to retrieve
size_t vertex_count;
size_t index_count;
Ogre::Vector3 *vertices;
unsigned long *indices;
// get the mesh information
GetMeshInformation(ent->getMesh(), vertex_count, vertices, index_count, indices,
ent->getParentNode()->_getDerivedPosition(),
ent->getParentNode()->_getDerivedOrientation(),
ent->getParentNode()->getScale());
// test for hitting individual triangles on the mesh
for (int i = 0; i < static_cast<int>(index_count); i += 3)
{
// check for a hit against this triangle
//std::pair<bool, Ogre::Real> hit = Ogre::Math::intersects(ray, vertices[indices[i]],
// vertices[indices[i+1]], vertices[indices[i+2]], true, false);
Vector3 noraml = Ogre::Math::calculateBasicFaceNormalWithoutNormalize (vertices[indices[i]], vertices[indices[i+1]], vertices[indices[i+2]] );
Vector3 center = (vertices[indices[i]] + vertices[indices[i+1]])/2;
center = (center+vertices[indices[i+2]] )/2;
mPoints.push_back(center);
mPoints.push_back(center + noraml );
}
// free the verticies and indicies memory
delete[] vertices;
delete[] indices;
/**////////////////////////////////////////////////////////////////////////
// Get the mesh information for the given mesh.
// Code found on this forum link: http://www.ogre3d.org/wiki/index.php/RetrieveVertexData
void DynLine::GetMeshInformation(const Ogre::MeshPtr mesh,
size_t &vertex_count,
Ogre::Vector3* &vertices,
size_t &index_count,
unsigned long* &indices,
const Ogre::Vector3 &position,
const Ogre::Quaternion &orient,
const Ogre::Vector3 &scale)
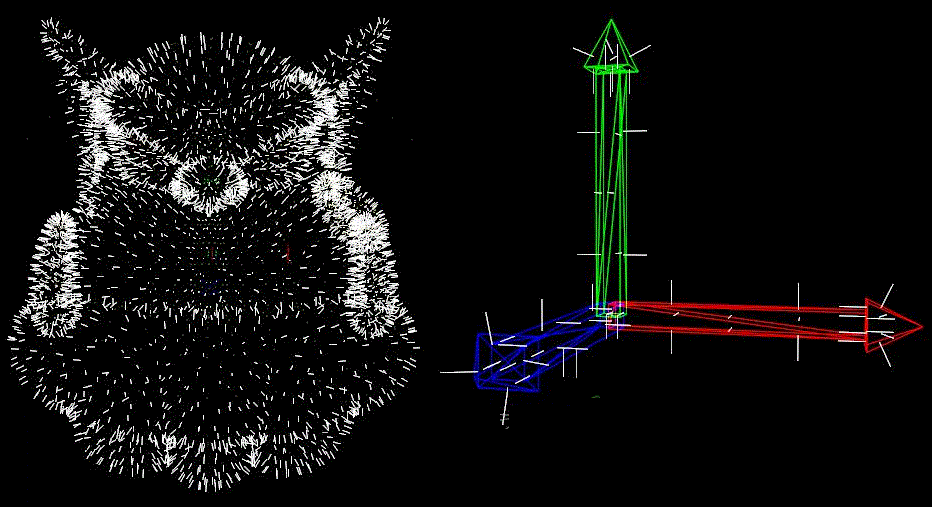
如此，上帝一一查明了世上的每一个生命，不管这个点式多么的渺小或微不足道，上帝均能一一检视。这里，在每一个面上都计算出了法线向量。
第五天，修改了Node要记得update。
void Node::needUpdate(bool forceParentUpdate)
