很多大公司的笔试题都会有一些逻辑题推理题,趁着今天公司不太忙,我把它整理一下,而且我的目标是把这些逻辑推理题各个击破,希望我提供的答案是正确的,以下是网上的逻辑推理题,我争取在每道题的下边公布出我的答案,至于说所用到的逻辑知识,我暂时说一下自己的情况吧,本人硕士毕业,有C/C+ code经验,对数据结构有简单的了解,并且对模拟/数字电路的概念,所以分析的时候可能会参考一些专业的推理方式来进行解答。
转载请注明出处:
http://www.cppblog.com/xinxin/archive/2009/11/24/101783.html很少有关于逻辑趣题的书出版,但乔治•萨默斯先生就奉献了两本(另一本为《逻辑推理新趣题》)。每本50 道精心设计的逻辑趣题,从易到难,顺次排列。后面最难的那几道题,就是解题专家,也会感到棘手。你大概还未曾有机会测试一下自己的逻辑推理能力吧?现在测试一下,怎么样?但愿每道题后所附的提示能帮你抵挡马上去翻书后答案的诱惑。顺便说一下,除了少数题目需要一些简单的初中代数知识外,只要求你有——灵活的思路和机智的推理。序 言本书中的趣题,都被写成“到底是谁干的”之类的短小谜案。每道趣题提供了若干线索,要求读者,或者说“侦探”,根据这些线索在一些不同的对象中判别出哪一个是题目要求寻找的对象(或者继续上面的比喻,在一些可疑分子中判定哪一个是真正的罪犯)。在这些趣题中,有些是真的要你去查出一个罪犯,但是绝大多数趣题只涉及基本上属于守法的公民或者纯粹的数字。解答这些趣题的一般方法是:在每道趣题末尾提出的问题中,陈述了要寻找的对象所必须满足的一个条件。例如,“第六号纸牌是A、K、Q 还是J?” 就是把“第六号纸牌”规定为一个条件。题目中的线索也或明或暗地规定着各个“可疑分子”所必须满足的条件。“侦探”要做的事,是发现全部的条件,然后判定哪一个——而且是唯一的一个——“可疑分子”,能够满足问题中陈述的条件。在这50 道趣题中,有40 道并不要求读者具有专门的知识。有些题目涉及一些数字,但并不需要代数知识。有10 道趣题需要用到简单的初中代数知识。
1、阿德里安、布福德和卡特三人去餐馆吃饭,他们每人要的不是火腿就是猪排。
(1)如果阿德里安要的是火腿,那么布福德要的就是猪排。
(2)阿德里安或卡特要的是火腿,但是不会两人都要火腿。
(3)布福德和卡特不会两人都要猪排。
谁昨天要的是火腿,今天要的是猪排?
答案:布福德昨天要的是火腿,今天要的是猪排。
推理如下:
假设阿德里要的是火腿,则由(1)知布福德要的必定是猪排。又由(2)知卡特要的是猪排。而由此又和(3)矛盾,故阿德里要的肯定是猪排;现在已经确定阿德里要的是猪排了,那么由(2)知卡特要的是火腿。由此可知每天阿德里必定要的是猪排,卡特必定要的是火腿,只有布福德每天可以要火腿或者要猪排都能够满足这三个条件。所以昨天要的是火腿,而今天要的是猪排的人必定是布福德。
2 、瓦尔、林恩和克里斯瓦尔、林恩和克里斯是亲缘关系,但他们之间没有违反伦理道德的问题。
(1)他们三人当中,有瓦尔的父亲、林恩唯一的女儿和克里斯的同胞手足。
(2)克里斯的同胞手足既不是瓦尔的父亲也不是林恩的女儿。
他们中哪一位与其他两人性别不同?
提示:以某一人为瓦尔的父亲并进行推断;若出现矛盾,换上另一个人。
答案:根据(1),三人中有一位父亲、一位女儿和一位同胞手足。如果瓦尔的父亲是克里斯,那么克里斯的同胞手足必定是林恩。于是,林恩的女儿必定是瓦尔。从而瓦尔是林恩和克里斯二人的女儿,而林恩和克里斯是同胞手足这是乱伦关系,是不允许的。因此,瓦尔的父亲是林恩。于是,根据(2),克里斯的同胞手足是瓦尔。从而,林恩的女儿是克里斯。再根据(1),瓦尔是林恩的儿子。因此,克里斯是唯一的女性。
3 、医务人员问题
“医院里的医务人员,包括我在内,总共是16 名医生和护士。下面讲到的人员情况,无论是否把我计算在内,都不会有任何变化。在这些医务人员中:
(1)护士多于医生。
(2)男医生多于男护士。
(3)男护士多于女护士。
(4)至少有一位女医生。”
这位说话的人是什么性别和职务?提示:确定一种不与题目中任何陈述相违背的关于男护士、女护士、男医生和女医生的人员分布情况。
答案:从(1)得知:护士至少有9 名,医生最多有7名。
又有(4)得知:男医生最多是6 名。于是,按照(2),男护士必定不到6 名,即男护士最多是5名。
根据(3),女护士少于男护士,所以女护士最多是4名;又由于护士至少是9名,则男护士最少是5名。
男护士最多是5名,男护士最少是5名,则男护士必定是5名。于是,护士必定不低于9 名,而女护士最多是4名,从而护士正好是9 名,包括5 名男性和4 名女性。
又根据(2),于是男医生则不能少于6 名。而医生最多有7名,且至少有一位女医生,这样,必定只有一位名女医生,6名男医生。
现在可以确定,有6名男医生,1名女医生,5名男护士,4名女护士。
如果把一名男医生排除在外,则与(2)矛盾;把一名男护士排除在外,则与(3)矛盾;把一名女医生排除在外,则与(4)矛盾;把一名女护士排除,则与任何一条都不矛盾。因此,说话的人是一位女护士。
4 、弗里曼先生的未婚妻
弗里曼先生认识埃达、比、茜德、黛布、伊芙这五位女士。
(1)五位女士分为两个年龄档:三位女士小于30 岁,两位女士大于30 岁。
(2)两位女士是教师,其他三位女士是秘书。
(3)埃达和茜德属于相同的年龄档。
(4)黛布和伊芙属于不同的年龄档。
(5)比和伊芙的职业相同。
(6)茜德和黛布的职业不同。
(7)弗里曼先生将同其中一位年龄大于30 岁的教师结婚。
谁是弗里曼先生的未婚妻?
提示:确定哪几位女士的年龄小于30 岁,哪几位女士是秘书。
答案:弗里曼的未婚妻是黛比女士。
推理过程:
以这五位女士的名字的首字母命名,可以分别将她们表示为ABCDE五个人。
由(3),假设A和C年龄大于30岁,又根据(1),则剩下的BDE应该都小于30岁;这与(4)中所说D和E属于不同的年龄档矛盾,故A和C年龄应该小于30岁。
现在已经知道A和C年龄小于30岁,而由(4)知道D和E应该是一个大于30,一个小于30 ,现在已经知道ACDE中有三个小于30岁的女士,所以B应该是大于三十岁的。这与才满足条件(1)。
由(5)B和E的职业相同,则她们必定都是女秘书,否则的话将和(6)矛盾,这和上边的推理过程是一样的。现在已经确定了B是大于三十岁的女秘书,而(7)告诉我们这其中必定有一位大于三十岁的女教师,且她就是弗里曼先生的未婚妻,现在可能另外一个大于三十岁的人只能在D和E中,而E确定是女秘书,所以另外一个大于三十岁的人必定是D,且为女教师,她就是弗里曼显示的未婚妻。
如果还要往下推理,可以得出:A 小于30岁教师;B大于三十岁秘书;C小于三十岁秘书;D大于三十岁教师;E小于三十岁秘书。
我做以上的推断时,用到了类似捆绑理论的观点。已经知道这里边年龄是3和2组合,而职业也是3和2组合,则由另个人年龄相同和另外另个人年龄不同可以确定相同年龄的两个人必定应该归到3的队伍里边去。呵呵,在网上搜了一下答案,还真的和我的不谋而合,看来啊,我这智商和思维模式都是普通之极啊
5、六个A 在这下面两个加法算式中,每个字母都代表0~9 的一个数字,而且不同的字母代表不同的数字。请问A 代表哪一个数字?提示:判定 A+B+C 和 A+D+E 的值。
这道题应该是题目不全,所以没法做了
6、 并非腰缠万贯
安妮特、伯尼斯和克劳迪姬是三位杰出的女性,她们各有一些令人注目的特点。
(1)恰有两位非常聪明,恰有两位十分漂亮,恰有两位多才多艺,恰有两位腰缠万贯。
(2)每位女性至多只有三个令人注目的特点。
(3)对于安妮特来说,下面的说法是正确的:如果她非常聪明,那么她也腰缠万贯。
(4)对于伯尼斯和克劳迪娅来说,下面的说法是正确的:如果她十分漂亮,那么她也多才多艺。
(5)对于安妮特和克劳迪娅来说,下面的说法是正确的:如果她腰缠万贯,那么她也多才多艺。
哪一位女性并非腰缠万贯?提示:判定哪几位女性多才多艺。
呵呵,目前为止xinxin我还没想出来呢
7、 网球选手
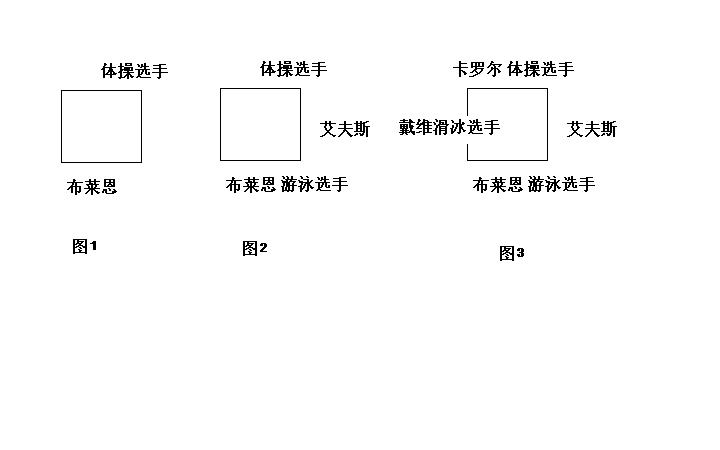
有两位女士,艾丽斯和卡罗尔,还有两位先生,布赖恩和戴维,他们四人都是运动员。其中一位是游泳选手,一位是滑冰选手,一位是体操选手,一位是网球选手。有一天,他们围着一张方桌而坐:(1)游泳选手坐在艾丽斯的左边。(2)体操选手坐在布赖恩的对面。(3)卡罗尔和戴维相邻而坐。(4)有一位女士坐在滑冰选手的左边。谁是网球选手?
提示:按姓名给出这四人的各种可能的坐法。然后确定可以把哪些运动项目分配给哪些人而不会与任何陈述发生矛盾。
xinxin的答案:爱丽丝为网球选手:
推理过程如下:从(2)可以画图1,再由(3)知道艾夫斯只能坐在布莱恩的左边或者右边,又有(1),所以爱丽丝一定坐在布莱恩的右边(如果坐在布莱恩的左边的话爱丽丝的左边则会是体操选手),且又有(1)知道布莱恩为游泳选手,即可画图2;又有4,知道女士卡罗尔必定是体操选手,所以戴维坐在布莱恩的左边,且为滑冰选手,所以知道艾里斯为网球选手
8 一轮牌安东尼、伯纳德和查尔斯三人玩了一轮牌,其中每盘只有一个赢家。(1)谁首先赢了三盘谁就是这一轮的赢家。(2)没有人连续赢两盘。(3)安东尼是第一盘的发牌者,但不是最后一盘的发牌者。(4)伯纳德是第二盘的发牌者。(5)他们三人围着桌子坐在固定的坐位上,按顺时针方向轮流发牌。(6)无论谁发牌,他发牌的那一盘都没赢。谁赢了这一轮牌?提示:判定总共玩了多少盘和谁赢了最后一盘。 9 三个D 在下面的乘法算式中,每个字母代表0~9 的一个数字,而且不同的字母代表不同的数字。请问D 代表哪一个数字?提示:首先判定111 的整数因子。 10 律师们的供词艾伯特、巴尼和柯蒂斯三人,由于德怀特被谋杀而受到传讯。犯罪现场的证据表明,可能有一名律师参与了对德怀特的谋杀。这三人中肯定有一人是谋杀者,每一名可疑对象所作的两条供词是:艾伯特:(1)我不是律师。(2)我没有谋杀德怀特。巴尼:(3)我是个律师。(4)但是我没有杀害德怀特。柯蒂斯:(5)我不是律师。(6)有一个律师杀了德怀特。**最后发现: Ⅰ.上述六条供词中只有两条是实话。 Ⅱ.这三个可疑对象中只有一个不是律师。是谁杀害了德怀特?提示:判定(2)和(4)这两条供词都是实话,还是其中只有一条是实话。 11 点子的排列方向正常的骰子,相对两面的点子数目之和总是7;就此而言,上图中的三只骰子是正常的。但是,从点子的排列方向来看,其中有一只与其他两只不同。在A、B、C 这三只骰子中,哪一只与其他两只不同?提示:判定哪些面上的点子可以有不同的排列方向;然后判定这些排列方向在不同的骰子中是否一致。 12 科拉之死科拉死了,是中毒死的。为此,安娜和贝思受到了**的传讯。安娜:如果这是谋杀,那肯定是贝思干的。贝思:如果这不是自杀,那就是谋杀。**作了如下的假定:(1)如果安娜和贝思都没有撒谎,那么这就是一次意外事故。(2)如果安娜和贝思两人中有一人撒谎,那么这就不是一次意外事故。最后的事实表明,这些假定是正确的。科拉的死究竟是意外事故,还是自杀,甚至是谋杀?提示:根据安娜的供词是真是假,判定科拉之死的性质;然后判定**的哪个假定能够适用。 13 兰瑟先生的坐位 “五对夫妇参加兰瑟先生的生日晚宴。坐位是按照如下图所示的L 形餐桌安排的:在餐桌周围:(1)每位男士坐在一位女士的对面。(2)我坐在坐位a,在我丈夫的对面。(3)没有一位女士坐在两位男士之间。(4)兰瑟先生坐在两位女士之间。兰瑟先生坐的是哪个坐位?” 注:“在两位男士(或女士)之间”,指的是沿桌子边缘,左侧是一位男士(或女士),右侧是另一位男士(或女士)。提示:先判定在不考虑具体坐位的情况下,五对夫妇围桌而坐的可能坐位安排;然后,从说话者的位置开始,判定具体坐位的安排情况。 14 被乘数首位变末位在下面这个乘法算式中,每个字母代表0~9 的一个数字,而且不同的字母代表不同的数字。有趣的是,把被乘数的首位数字移作末位数字,就变成了积。 M 代表哪一个数字?提示:选择M 和A 的值以判定其他字母的相应值。 15 单 张多拉、洛伊丝和罗斯玩一种纸牌游戏,一共35 张牌,其中有17 个对子,还有一个单张。(1)多拉发牌,先给洛伊丝一张,再给罗斯一张,然后给自己一张;如此反复,直到发完所有的牌。(2)在每个人把手中成对的牌打出之后,每人手中至少剩下一张牌,而三人手中的牌总共是9 张。(3)在剩下的牌中,洛伊丝和多拉手中的牌加在一起能配成的对子最多,罗斯和多拉手中的牌加在一起能配成的对子最少。单张发给了谁?提示:判定给每个人发了几张牌以及每两个人手中的牌加在一起能配成的对子的数目。 16 姐妹俩阿格尼丝、贝齐、辛迪、迪莉娅这四位女士在工作间歇去用了些咖啡点心,正在付款。(1)有两位女士,身上带有的硬币各为60 美分,都是银币,且枚数相同,但彼此间没有一枚硬币面值相同。(2)有两位女士,身上带有的硬币各为75 美分,都是银币,且枚数相同,但彼此间没有一枚硬币面值相同。(3)阿格尼丝的账单是10 美分,贝齐的账单是20 美分,辛迪的账单是 45 美分,迪莉娅的账单是55 美分。(4)每位女士都一分不少地付了账,而且不用找零。(5)有两位女士是姐妹俩,她们付账后剩下的硬币枚数相同。哪两位女士是姐妹?注:“银币”是指5 美分、10 美分、25 美分或50 美分的硬币。提示:先判定四种符合题意的持币情况,然后判定每人符合哪种情况。 17 第二次联赛艾伦、巴特、克莱、迪克和厄尔每人都参加了两次网球联赛。(1)每次联赛只进行了四场比赛:艾伦对巴特艾伦对厄尔克莱对迪克克莱对厄尔(2)只有一场比赛在两次联赛中胜负情况保持不变。(3)艾伦是第一次联赛的冠军。(4)在每一次联赛中,输一场即被淘汰,只有冠军一场都没输。谁是第二次联赛的冠军?注:每场比赛都不会有平局的情况。提示:从一个人必定胜的比赛场数,判定在第一次联赛中每一场的胜负情况;然后判定哪一位选手在两场联赛中输给了同一个人。 18 缺失的数字在下列加法算式中,每个字母代表0~9 的一个数字,而且不同的字母代表不同的数字:请问缺了0~9 中的哪一个数字?提示:从 A、E 和 F 的值判定 B 的可能值;然后判定从 C+C 是否进位。 19 见习医生的一星期有三位见习医生,他们在同一家医院中担任住院医生。(1)一星期中只有一天三位见习医生同时值班。(2)没有一位见习医生连续三天值班。(3)任两位见习医生在一星期中同一天休假的情况不超过一次。(4)第一位见习医生在星期日、星期二和星期四休假。(5)第二位见习医生在星期四和星期六休假。(6)第三位见习医生在星期日休假。三位见习医生星期几同时值班?提示:判定星期日、星期二和星期四是谁值班;然后判定在题目中没有提到的三天中分别是谁休假。 20 电影主角亚历克斯•怀特有两个妹妹:贝尔和卡斯;亚历克斯•怀特的女友费伊•布莱克有两个弟弟:迪安和埃兹拉。他们的职业分别是:亚历克斯:舞蹈家迪安:舞蹈家怀特家 贝尔:舞蹈家布莱克家埃兹拉:歌唱家卡斯:歌唱家费伊:歌唱家六人中有一位担任了一部电影的主角;其余五人中有一位是该片的导演。(1)如果主角和导演是亲属,则导演是个歌唱家。(2)如果主角和导演不是亲属,则导演是位男士。(3)如果主角和导演职业相同,则导演是位女士。(4)如果主角和导演职业不同,则导演姓怀特。(5)如果主角和导演性别相同,则导演是个舞蹈家。(6)如果主角和导演性别不同,则导演姓布莱克。谁担任了电影主角?提_________示:根据陈述中的假设与结论,判定哪三个陈述组合在一起不会产生矛盾。 21 鼓 手有两位女士,阿琳和谢里尔,有两位男士,伯顿和唐纳德,他们都是音乐家。一位是钢琴手,另一位是小提琴手,第三位是长笛手,第四位是鼓手。有一天他们围着方桌而坐:(1)坐在伯顿对面的是钢琴手。(2)坐在唐纳德对面的不是长笛手。(3)坐在阿琳左侧的是小提琴手。(4)坐在谢里尔左侧的不是鼓手。(5)长笛手与鼓手是夫妻。谁是鼓手?提示:按姓名给出这四人的各种可能的坐法。然后确定可以把哪些音乐专长分配给哪些人而不会与任何陈述发生矛盾。 22 左邻右舍奥斯汀、布鲁克斯和卡尔文三人住在一幢公寓的同一层上。一人的房间居中,与其他两人左右相邻。(1)每人都只养了一只宠物:不是狗就是猫;每人都只喝一种饮料:不是茶就是咖啡;每人都只采用一种抽烟方式:不是烟斗就是雪茄。(2)奥斯汀住在抽雪茄者的隔壁。(3)布鲁克斯住在养狗者的隔壁。(4)卡尔文住在喝茶者的隔壁。(5)没有一个抽烟斗者喝茶。(6)至少有一个养猫者抽烟斗。(7)至少有一个喝咖啡者住在一个养狗者的隔壁。(8)任何两人的相同嗜好不超过一种。谁住的房间居中?提示:判定哪些三嗜好组合可以符合这三人的情况;然后判定哪一个组合与住在中间的人相符合。 23 三个城市阿灵顿、布明汉和坎顿韦尔这三个城市,它们的形状都呈长方形。(1)每个城市沿边界街段(指两条平行街道之间的一段街道)的数目都是整数,而且市内街段总是都与沿边界的街段平行。(2)沿城市北部边界的街段的数目,阿灵顿最少,布明汉比阿灵顿多3 段,坎顿韦尔又比布明汉多3 段。(3)有两个城市,它们市内街段的数目,等于沿整个边界的街段的数目。哪个城市其市内街段的数目不等于沿整个边界的街段的数目?提示:列出表示一个城市沿整个边界的街段的数目的代数式和表示市内街段的数目的代数式;然后求出使两者相等的整数解。 24 骰子面的方位正常的骰子,相对两面的点子数目之和总是7;就此而言,上图中的三只骰子是正常的。但是,从各个面的方位来看,其中有一只与其他两只不同。在A、B、C 这三只骰子中,哪一只与其他两只不同?注:如果你觉得难以同时看到骰子的六个面,可以照下图画出骰子的多面图。这样除了底下的一面外,其他各面都可同时看到。提示:翻动这三个立方体,使相同的相邻面处于同样的空间方位;然后判定其余面上的点数。 25 需要找零阿莫斯、伯特、克莱姆、德克四人刚刚在一家餐馆吃完午餐,正在付账。(1)这四人每人身上所带的硬币总和各为1 美元,都是银币,而且枚数相等。(2)25 美分的硬币,阿莫斯有三枚,伯特有两枚,克莱姆有一枚,德克一枚也没有。(3)四人要付的款额相同。其中三人能如数付清,不必找零,但另一个人却需要找零。谁需要找零?注:“银币”是指5 美分、10 美分、25 美分或50 美分的硬币。提示:先判定每个人所带硬币的枚数;然后判定什么款额不能使四个人都不用找零。 26 谁是医生布兰克先生有一位夫人和一个女儿;女儿有一位丈夫和一个儿子。这些人有如下的情况:(1)五人中有一人是医生,而在其余四人中有一人是这位医生的病人。(2)医生的孩子和病人父母亲中年龄较大的那一位性别相同。(3)医生的孩子(3a)不是病人,(3b)不是病人父母亲中年龄较大的那一位。谁是医生?提示:分别判定谁不可能是医生,谁不可能是病人;然后判定在某人是医生的情况下,谁不能是病人。 27 乘积首位变末位下面这个乘法算式中,每个字母代表0~9 的一个数字,而且不同的字母代表不同的数字。有趣的是,把乘积的首位数字移作末位数字,就成为被乘数。 M 代表哪一个数字?提示:选择M 和A 的值以判定F 和B 的相应值。然后用已经确定的数值去判定余下字母的相应值。 28 健身俱乐部肯和利兹是在一家健身俱乐部首次相遇并相互认识的。(1a)肯是在一月份的第一个星期一那天开始去健身俱乐部的。(1b)此后,肯每隔四天(即第五天)去一次。(2a)利兹是在一月份的第一个星期二那天开始去健身俱乐部的。(2b)此后,利兹每隔三天(即第四天)去一次。(3)在一月份的31 天中,只有一天肯和利兹都去了健身俱乐部,正是那一天他们首次相遇。肯和利兹是在一月份的哪一天相遇的?提示:判定利兹是在肯之前还是之后开始去健身俱乐部的;然后判定肯和利兹是从哪一天开始去健身俱乐部的。 29 达纳之死达纳溺水死亡,为此,阿洛、比尔和卡尔被一位警探讯问。(1)阿洛说:如果这是谋杀,那肯定是比尔干的。(2)比尔说:如果这是谋杀,那可不是我干的。(3)卡尔说:如果这不是谋杀,那就是自杀。(4)警探如实地说:如果这些人中只有一个人说谎,那么达纳是自杀。达纳是死于意外事故,还是自杀,甚至是谋杀?提示:在分别假定陈述(1)、陈述(2)和陈述(3)为谎言的情况下,推断达纳的死亡原因;然后判定这些陈述中有几条能同时为谎言。 30 最后一个划船渡河的人三个男人和两个女人要渡过一条河,但渡河的小船只能坐两个人。(1)女人们要求:任何时候都不能让一个女人单独地和一个男人在一起。(2)每次渡河只能有一个人划船。因此,男人们要求:不能让一个人连续划船两次。(3)船上只有一个人独自划船的情况,先是轮到阿特,其次是本,第三是考尔。谁最后一个划船渡河?注:要求以尽可能少的次数渡河。提示:确定从原岸向对岸渡河时船上只有两个男人或只有两个女人的一种方案。 31 倒霉者哈里和妻子哈丽雅特举办晚餐会,邀请的客人有:弟弟巴里和他的妻子巴巴拉;妹妹萨曼莎和她的丈夫塞缪尔;还有邻居内森和他的妻子纳塔利。在他们全都就席之后,不慎有一碗汤泼在某个人身上。餐桌周围的坐位安排如下图所示:(1)被泼了一身汤的倒霉者坐在标有V 的坐位上。(2)每位男士都坐在一位女士的对面。(3)每位男士都坐在一位男士与一位女士之间。(4)没有任何男士坐在自己妻子的对面。(5)男主人坐在倒霉者的右侧。(6)巴里坐在女主人的旁边。(7)萨曼莎坐在倒霉者配偶的旁边。谁是倒霉者?提示:先判定在不考虑具体人物的情况下,人们围桌而坐的可能坐位安排;然后,从男主人的坐位开始,判定各人具体的坐位安排。 32 最小的和在下面的三个加法算式中,每个字母都代表0~9 的一个数字,而且不同的字母代表不同的数字。但是,每个字母在一个加法算式中所代表的数字,并不一定和它在其他加法算式中所代表的数字相同。哪一个加法算式的和最小,是Ⅰ,是Ⅱ,还是Ⅲ?提示:在每个加法算式中都有一个字母,它们的表现与同一个数字相关联。先确定这个数字,然后求出在每个加法算式中与它相关联的其他两个数字。说得更具体些,可将每个算式的右数第一列同其第三列加以比较。 33 李、戴尔、特里和马里恩李、戴尔、特里和马里恩是亲缘关系,但他们之间没有违反伦理道德的问题。(1)其中有一个人与其他三人的性别不同。(2)在这四个人中,有李的母亲、戴尔的哥哥、特里的父亲和马里恩的女儿。(3)最年长的与最年轻的性别不同。谁与其他三人性别不同?提示:要末母亲和女儿是指同一个人,要末父亲和哥哥是指同一个人。假定其中一种情况,继续进行推断。 34 圈出的款额两位女士和两位男士走进一家自助餐厅,每人从机器上取下一张如下图所示的标价单。 50 95 45 90 40 85 35 80 30 75 25 70 20 65 15 60 10 55 (1)四个人要的是同样的食品,因此他们的标价单被圈出了同样的款额(以美分为单位)。(2)每人都只带有四枚硬币。(3)两位女士所带的硬币价值相等,但彼此间没有一枚硬币面值相同;两位男士所带的硬币价值相等,但彼此间也没有一枚硬币面值相同。(4)每个人都能按照各自标价单上圈出的款额付款,不用找零。在每张标价单中圈出的是哪一个数目?注:“硬币”可以是1 美分、5 美分、10 美分、25 美分、50 美分或1 美元(合100 美分)。提示:设法找出所有这样的两组硬币(硬币组对):每组四枚,价值相等,但彼此间没有一枚硬币面值相同。然后从这些组对中判定能付清账目而不用找零的款额。 35 谁是教授阿米莉亚、比拉、卡丽、丹尼斯、埃尔伍德和他们的配偶参加在情侣餐馆中举行的一次大型聚会。这五对夫妇被安排坐在一张L 形的桌子的周围,如下图:(1)阿米莉亚的丈夫坐在丹尼斯妻子的旁边。(2)比拉的丈夫是唯一单独坐在桌子的一个边上的男士。(3)卡丽的丈夫是唯一坐在两位女士之间的男士。(4)没有一位女士坐在两位女士之间。(5)每位男士都坐在自己妻子的对面。(6)埃尔伍德的妻子坐在教授的右侧。谁是教授?注:“在两位女士之间”,指的是沿桌子边缘,左侧是一个女士,右侧是另一个女士。提示:先判定在不考虑具体人物的情况下,五对夫妇围桌而坐的可能坐位安排;然后再确定具体人物的坐位就比较容易了。 36 三个J 在下列的加法算式中,每个字母代表0~9 的一个数字,而且不同的字母代表不同的数字。 J 代表哪一个数字?注:假定A、D 和C 都不能为0。提示:在J 为某些特定值的情况下,判定每一列的可能的和;然后把这三个和与J 相加,看看其总和是否等于45。 37 谁没有输过多丽丝、劳拉、雷内三人玩了两盘纸牌游戏,其玩法是:(a)通过抽牌来配成对子,(b)尽量避免手中只留下一个单张。游戏者轮流从别人手中抽牌,直到有一人手中只剩下一个单张,此人便是输者。在抽牌后配成了对子,便打出这对牌。如果一个人从第二个人手中抽了一张牌并打出一个对子之后,手中已经无牌,则轮到第三个人抽牌时就从第二个人手中抽。在每一盘接近尾声的时候:(1)多丽丝只有一张牌,劳拉只有两张牌,雷内也只有两张牌;这五张牌包括两个对子和一个单张,但任何人手中都没有对子。(2)多丽丝从劳拉手中抽了一张牌,但没能配成对。(3)劳拉从雷内手中抽了一张牌,随后雷内从多丽丝手中抽了一张牌。(4)在任何一盘中,没有一人手中两次拿着同样的一手牌。(5)没有一人连输两盘。在两盘游戏中,谁没有输过?提示:判定三人手中纸牌的可能分布;然后判定一盘游戏该怎样进行才能做到没有一人手中两次拿着同样的一手牌。 38 谁是凶手阿伦•格林的妹妹是贝蒂和克拉拉;他女友弗洛拉•布朗的哥哥是杜安和埃德温。他们的职业是:阿伦:医生杜安:医生格林家 贝蒂:医生布朗家埃德温:律师克拉拉:律师弗洛拉:律师这六人中的一人杀了其余五人中的一人。(1)如果凶手与受害者有亲缘关系,则凶手是男性。(2)如果凶手与受害者没有亲缘关系,则凶手是个医生。(3)如果凶手与受害者职业相同,则受害者是男性。(4)如果凶手与受害者职业不同,则受害者是女性。(5)如果凶手与受害者性别相同,则凶手是个律师。(6)如果凶手与受害者性别不同,则受害者是个医生。谁是凶手?提示:根据陈述中的假设与结论,判定哪三个陈述组合在一起不会产生矛盾。 39 没有出黑桃男女二人玩一种纸牌游戏:(a)在可能的情况下,后手在每一圈(即先后各出一张牌)中都必须按先手出的花色出牌,而先手则可以随意出牌;(b)每一圈的胜方即为下一圈的先手。(1)双方手中各有四张牌,其花色分布是:男方手中:黑桃—黑桃—红心—梅花;女方手中:方块—方块—红心—黑桃。(2)双方都各做了两次先手。(3)双方都各胜了两圈。(4)在每一圈中先手出的花色都不一样。(5)在每一圈中都出了两种不同的花色。在打出的这四圈牌中,哪一圈没有出黑桃?注:王牌至少胜了一圈。(王牌是某一种花色中的任何一张牌,它可以:(a)在手中没有先手出的花色的情况下,出王牌——这样,一张王牌将击败其他三种花色中的任何牌;(b)与其他花色的牌一样作为先手出的牌。)提示:从先手和胜方的可能序列中判定王牌的花色;然后判定在哪一圈时先手出了王牌并取胜。最后判定在哪一圈时出了黑桃。 40 勒索者海伦和她的丈夫赫尔穆特举行晚餐会,邀请的客人有:她的弟弟布莱尔和布莱尔的妻子布兰奇;她的姐姐希拉和希拉的丈夫舍曼;邻居诺拉和诺拉的丈夫诺顿。八人之中有一人是勒索者,其他七人之中有一人是勒索者的受害者。当他们全部在桌旁就坐的时候,受害者试图用切牛排的餐刀去刺勒索者,但没有成功。围绕桌子的坐位安排,如下图所示:(1)勒索者坐在坐位E。(2)受害者坐在坐位V。(3)每位男士坐在一位女士的对面。(4)每位男士坐在一位男士和一位女士之间。(5)勒索者的配偶与受害者的配偶相邻而坐。(6)男主人坐在受害者与女主人之间。(7)布莱尔坐在希拉与诺顿之间。谁是勒索者?提示:在不考虑具体人物的情况下,判定人们坐位的各种可能安排;然后,通过逐步判定各个具体人物的坐位,把这些可能的安排减少到剩下唯一的一种。 41 没有放上的数字有人把0~9 这十个数字中的九个用字母代表,如上图那样放在两个三角形的每一个周围。(1)三角形各边上四个数字之和为14。(2)在第一个三角形中没有放上的数字,不同于在第二个三角形中没有放上的数字。在两个三角形中没有放上的是十个数字中的哪两个?提示:建立一个方程,把没有放上的数字同三个角上的数字之和联系起来。(注意把三条边上的数字之和加起来时,三个角上的数字用了两次。)然后,根据可能的三个角数字之和,判定各个角上的可能的数字。最后判定放在各个角之间的数字。 42 指认罪犯**叫四个男人排成一行,然后让一位目击者从这四个人中辨认出一个罪犯。目击者寻找的男人,长得不高,不白,不瘦,也不漂亮,尽管这些特征中的任何一个都可能让人拿不准。在这一排人之中:(1)四个男人每人身旁都至少站着一个高个子。(2)恰有三个男人每人身旁至少站着一个皮肤白皙的人。(3)恰有两个男人每人身旁至少站着一个骨瘦如柴的人。(4)恰有一个男人身旁至少站着一个长相漂亮的人。在这四个男人中:(5)第一个皮肤白皙,第二个骨瘦如柴,第三个身高过人,第四个长相漂亮。(6)没有两个男人具有一个以上的共同特征(即高个、白皙、消瘦、漂亮)。(7)只有一个男人具有两个以上的寻找特征(即不高、不白、不瘦、不漂亮)。此人便是目击者指认的罪犯。目击者指认的罪犯是哪一个人——是第一个,第二个,第三个,还是第四个?提示:判定在四个人排成的一行中,高个、白皙、消瘦、漂亮者的可能位置。然后判定每个男人的全部可能特征。最后,辨出只具备高个、白皙、消瘦、漂亮这四个特征中的一个的男人。 43 最后一个划船过湖的人四个男人和四个女人要渡过一个湖,但他们的那条小船只能坐三个人。(1)女人们要求:任何时候都不能让一个女人单独地和一个男人在一起。(2)每次摆渡只能有一个人划船。因此,男人们要求:不能让一个人连续划船两次。(3)大家一致认为:不应该让女人划船。(4)亚伯拉罕轮到第一个划船,巴雷特其次,克林顿在第三,道格拉斯最后。(5)在每次划回原地时,船上只有一个划船的人。谁最后一个划船渡过湖泊?注:假定以尽可能少的次数渡过湖泊。提示:判定一种划船过湖的方案,其中有一个男人在第一次过湖时不是他划船,从而在第二次过湖(返回原地)时他能够在船上并且是他划船,而且,有一个男人在倒数第二次过湖(返回原地)时不是他划船,从而在最后一次过湖时他能够在船上并且是他划船。 44 第六号纸牌八张编了号的纸牌扣在桌上,它们的相对位置如下图所示:这八张纸牌:(1)每张A 挨着一张K。(2)每张K 挨着一张Q。(3)每张Q 挨着一张J。(4)没有一张Q 与A 相邻。(5)没有两张相同的牌彼此相邻。(6)八张牌中有两张A,两张K,两张Q,两张J。编为第六号的是哪一种牌——是A、K、Q 还是J?提示:假定第六号牌分别是A、K、Q 或J。只在一种情况下不会产生矛盾。 45 最短的时间一天晚上,威尔逊、泽维尔、约曼、曾格和奥斯本五人沿着一条河岸分别扎下帐篷露营。翌日早晨,前四人都到奥斯本的帐篷碰头,然后各自返回自己的帐篷。(1)威尔逊和泽维尔的帐篷在奥斯本帐篷的下游,约曼和曾格的帐篷在奥斯本帐篷的上游。(2)威尔逊、泽维尔、约曼和曾格各有一艘汽艇;如果河水静止不动,每艘汽艇只用一个小时便可把主人带到奥斯本的帐篷。(3)河流非常湍急。(4)翌日早晨,四人驾汽艇抵达奥斯本帐篷所花的时间,威尔逊是75 分钟,泽维尔是70 分钟,约曼是50 分钟,曾格是45 分钟。四人中谁花在往返路程上的时间最短?提示:把每个人逆流而上和顺流而下所需的时间列成代数方程;然后解出各人返回自己帐篷所需的时间。 46 仁爱的人亚当、布拉德和科尔是三个不同寻常的人,每个人都恰有三个不同寻常的特点。(1)两个人非常聪明,两个人非常漂亮,两个人非常强壮,两个人非常诙谐,一个人非常仁爱。(2)对于亚当来说,下面是说法是正确的:(2a)如果他非常诙谐,那么他也非常漂亮;(2b)如果他非常漂亮,那么他不是非常聪明。(3)对于布拉德来说,下面的说法是正确的:(3a)如果他非常诙谐,那么他也非常聪明;(3b)如果他非常聪明,那么他也非常漂亮。(4)对于科尔来说,下面的说法是正确的:(4a)如果他非常漂亮,那么他也非常强壮;(4b)如果他非常强壮,那么他不是非常诙谐。谁非常仁爱?提示:判定每个人的特点的可能组合。然后分别假定亚当、布拉德或科尔具有仁爱的特点。只有在一种情况下,不会出现矛盾。 47 “老处女” 多萝西、洛雷塔、罗莎琳三位女士玩一种叫做“老处女”的纸牌游戏,其玩法是:(a)通过抽牌来配成对子,(b)尽量避免手中只留下一个单张,即所谓“老处女”。游戏者轮流从别人手中抽牌,直到有一人手中只剩下一个“老处女”,此人便是输者。在抽牌后配成了对子,便打出这对牌。如果一个人从第二个人手中抽了一张牌并打出一个对子之后,手中已经无牌,则轮到第三个人抽牌时就从第二个人手中抽。在一盘游戏接近尾声时:(1)多萝西只有一张牌,洛雷塔只有两张牌,罗莎琳只有四张牌;这七张牌包括三个对子和一个单张,但任何人手中都没有对子。(2)多萝西从另一人手中抽了一张牌,可是没能配成对。(3)刚被多萝西抽走一张牌的那个人,接着从第三人手中抽了一张牌。(4)没有一人两次拿着同样的一手牌。(5)这一盘游戏自此在抽了五次牌(包括上面(2)、(3)这两次)后便告结束。谁的手中留下了“老处女”?提示:判定三个人手中的纸牌分布;然后判定怎样才能进行得既没有任何一人两次拿着同样的一手牌,又恰好经过五次抽牌便告结束。 48 史密斯家的人有两位女士,奥德丽和布伦达,还有两位男士,康拉德和丹尼尔,他们每人每星期(从星期日到星期六)都有两天做健美操。在一个星期中:(1)奥德丽在某天做了健美操后过五天再做健美操(即有四天不做,到第五天再做。下同)。(2)布伦达在某天做了健美操后过四天再做健美操。(3)康拉德在某天做了健美操后过三天再做健美操。(4)丹尼尔在某天做了健美操后过两天再做健美操。(5a)史密斯家的一男一女只有一次在同一天做健美操。(5b)在其余的日子里,每天都只有一个人做健美操。哪两位是史密斯家的人?提示:判定两位女士可能在哪四天做健美操;然后判定在余下的三天中每天是哪位男士做健美操。最后在女士做健美操的四天中判定有哪一天一位男士也可做健美操。 49 应 聘奥尔登、布伦特、克雷格、德里克四人应聘一个职务,此职务的要求条件是:高中毕业至少两年的工作经验退伍军人具有符合要求的证明书谁满足的条件最多,谁就被雇用。(1)把上面四个要求条件两两配对,可配成六对。每对条件都恰有一人符合。(2)奥尔登和布伦特具有同样的学历。(3)克雷格和德里克具有同样的工作年限。(4)布伦特和克雷格都是退伍军人。(5)德里克具有符合要求的证明书。谁被雇用了?提示:画一张如下的表格,其中大写字母分别代表那四个人,g 代表学历,w 代表工作年限,v 代表退伍军人,r 代表有符合要求的证明书。然后,如果一个人满足某项要求,就在相应的格子中填上X;如果一个人不能满足某项要求,则在相应的格子中填上O。排除那些无人能满足某对要求的表格。 50 罪恶累累阿斯特夫妇、布赖斯夫妇和克兰夫妇,六人围桌而坐,如下图所示。在桌子周围:(1)恰有三人身旁至少坐着一个谋杀犯。(2)恰有四人身旁至少坐着一个勒索犯。(3)恰有五人身旁至少坐着一个诈骗犯。(4)恰有六人身旁至少坐着一个盗窃犯。关于犯罪类型:(5)没有两人同犯一种以上的罪行。(6)有一个人犯的罪多于其他人。关于各个人物:(7)阿斯特和他的妻子都只犯了一种罪,尽管是不同的罪。(8)布赖斯和他的妻子都是诈骗犯。(9)克兰和他的妻子都是盗窃犯。(10)犯诈骗罪的女人多于男人。谁犯的罪最多?提示:分别判定谋杀犯、勒索犯、诈骗犯和盗窃犯的可能坐法。然后判定犯四种罪行的人的数目、犯三种罪行的人的数目、犯两种罪行的人的数目和只犯一种罪行的人的数目。最后判定每个人的具体犯罪类型。答 案 1.昨天火腿,今天猪排根据(1)和(2),如果阿德里安要的是火腿,那么布福德要的就是猪排,卡特要的也是猪排。这种情况与(3)矛盾。因此,阿德里安要的只能是猪排。于是,根据(2),卡特要的只能是火腿。因此,只有布福德才能昨天要火腿,今天要猪排。 2.瓦尔、林恩和克里斯根据(1),三人中有一位父亲、一位女儿和一位同胞手足。如果瓦尔的父亲是克里斯,那么克里斯的同胞手足必定是林恩。于是,林恩的女儿必定是瓦尔。从而瓦尔是林恩和克里斯二人的女儿,而林恩和克里斯是同胞手足,这是乱伦关系,是不允许的。因此,瓦尔的父亲是林恩。于是,根据(2),克里斯的同胞手足是瓦尔。从而,林恩的女儿是克里斯。再根据(1),瓦尔是林恩的儿子。因此,克里斯是唯一的女性。 3.医务人员由于医生和护士的总数是16 名,从(1)和(4)得知:护士至少有9 名,男医生最多是6 名。于是,按照(2),男护士必定不到6 名。根据(3),女护士少于男护士,所以男护士必定超过4 名。根据上述推断,男护士多于4 名少于6 名,故男护士必定正好是5 名。于是,护士必定不超过9 名,从而正好是9 名,包括5 名男性和4 名女性,于是男医生则不能少于6 名。这样,必定只有一测试你的逻辑推理能力名女医生,使得总数为16 名。如果把一名男医生排除在外,则与(2)矛盾;把一名男护士排除在外,则与(3)矛盾;把一名女医生排除在外,则与(4)矛盾;把一名女护士排除,则与任何一条都不矛盾。因此,说话的人是一位女护士。 4.弗里曼先生的未婚妻根据(1)、(3)和(4),黛布和伊芙当中必定有一位与埃达和茜德属于同一个年龄档;因此,埃达和茜德都小于30 岁。按照(7),弗里曼先生不会与埃达或茜德结婚。根据(2)、(5)和(6),茜德和黛布当中必定有一位与比和伊芙从事同样的职业;因此,比和伊芙是秘书。按照(7),弗里曼先生不会与比或伊芙结婚。排除以上四位,弗里曼先生将和黛布女士结婚,她必定是一位年龄大于30 岁的教师。从以上的推理中,我们还可以知道其他四位女士的情况:伊芙必定小于 30 岁,比必定大于30 岁;茜德必定是位秘书,而埃达必定是位教师。 5.六个A A+B+C 或A+D+E 都不可能大于27(即9+9+9)。因为G、H 和I 代表不同的数字,所以,右列要给中列进位一个数,而中列也要给左列进位一个数,并且这两个进位的数不能相同。在一列的和小于或等于27 的情况下,唯一能满足这种要求的是一列的和为19。因此,A+B+C 或A+D+E 必定等于19。于是,F G H I 等于2109。排除了0、1、2、9 这四个数字之后,哪三个不同数字之和为19 呢?经过试验,可以得出这样的两组数字:4、7、8 与5、6、8。因此,A 代表8。两种可能的加法是: 6.并非腰缠万贯根据(3)和(5),如果安妮特非常聪明,那她也多才多艺。根据(5),如果安妮特富有,那她也多才多艺。根据(1)和(2),如果安妮特既不富有也不聪明,那她也是多才多艺。因此,无论哪一种情况,安妮特总是多才多艺。根据(4),如果克劳迪娅非常漂亮,那她也多才多艺。根据(5),如果克劳迪娅富有,那她也多才多艺。根据(1)和(2),如果克劳迪娅既不富有也不漂亮,那她也是多才多艺。因此,无论哪一种情况,克劳迪娅总是多才多艺。于是,根据(1),伯尼斯并非多才多艺。再根据(4),伯尼斯并不漂亮。从而根据(1)和(2),伯尼斯既聪明又富有。再根据(1),安妮特和克劳迪娅都非常漂亮。于是根据(2)和(3),安妮特并不聪明。从而根据(1),克劳迪娅很聪明。最后,根据(1)和(2),安妮特应该很富有,而克劳迪娅并非腰缠万贯。 7.网球选手根据(3),这四个人的坐法有4 种可能(A 代表艾丽斯,B 代表布赖恩, C 代表卡罗尔,D 代表戴维):根据(1)和(2),Ⅰ和Ⅱ可以排除,而Ⅲ和Ⅳ变成:根据(4),Ⅲ可排除,而且滑冰选手必定是戴维。因此,艾丽斯是网球选手。 8.一轮牌根据(1)和(2),至少玩了5 盘;根据(1)和(3),最多玩了6 盘。如果是玩了5 盘,那么根据(2),这一轮的赢家必然赢了第一、第三和第五盘。但是,根据(3)、(4)和(5),在这三盘中,每人必定会轮上一次发牌。这样,与(6)发生矛盾,因此无疑是玩了6 盘。由于是玩了6 盘,根据(3)、(4)和(5),查尔斯是最后一盘也就是第六盘的发牌者。根据(1),最后一盘也就是第六盘的赢家便是这一轮的赢家;于是根据(6),安东尼或伯纳德赢了最后一盘也就是第六盘,是这一轮的赢家。如果安东尼赢了第六盘,根据(6),他就不会赢第一盘或第四盘;而根据(2),他也不会赢第五盘。于是,他只会赢了第二和第三盘,这种情况与(2)有矛盾。因此,安东尼在第六盘中没有获胜。这样,伯纳德必定赢了第六盘,也就是说伯纳德是这一轮的赢家。这一轮牌中按各盘获胜者排出的序列可能有4 种(A 代表安东尼,B 代表伯纳德,C 代表查尔斯):发牌者A B C A B C Ⅰ 获胜者B A B C A B Ⅱ 获胜者B C B C A B Ⅲ 获胜者B C A B A B Ⅳ 获胜者B C A B C B 9.三个D A×CB=DDD。 A×CB=D×111。 A×CB=D×3×37。因而CB 为37 或74(即2×37)。如果CB 为37,则A=3D。如果CB 为74,则2A=3D。于是A、B、C 和D 的值有六种可能,如下表: CB D A (a)37 1 3 (b)37 2 6 (c)37 3 9 (d)74 2 3 (e)74 4 6 (f)74 6 9 由于每个字母各代表一个不同的数字,(a)、(c)、(e)这三种可能可以排除。以(b)、(d)、(f)的数值作实际运算,可以确定在每种情况下E、 F 和C 所代表的数字。我们得到如下三个式子:其中只有(b)是每个字母各代表一个不同的数字。所以D 代表数字2。 10.律师们的供词供词(2)和(4)之中至少有一条是实话。如果(2)和(4)都是实话,那就是柯蒂斯杀了德怀特;这样,根据Ⅰ,(5)和(6)都是假话。但如果是柯蒂斯杀了德怀特,(5)和(6)就不可能都是假话。因此,柯蒂斯并没有杀害德怀特。于是,(2)和(4)中只有一条是实话。根据Ⅱ,(1)、(3)和(5)中不可能只有一条是实话。而根据Ⅰ,现在(1)、(3)和(5)中至多只能有一条是实话。因此(1)、(3)和(5)都是假话,只有(6)是另外的一条真实供词了。由于(6)是实话,所以确有一个律师杀了德怀特。还由于:根据前面的推理,柯蒂斯没有杀害德怀特;(3)是假话,即巴尼不是律师;(1)是假话,即艾伯特是律师。从而,(4)是实话,(2)是假话,而结论是:是艾伯特杀了德怀特。 11.点子的排列方向无论骰子怎样摆,一点、四点和五点的排列方向总是不变的。但是,两点、三点和六点却可以有如下不同的排列方向:以下的推理,是以相对两面点数之和为7 的事实为依据的。如果骰子B 和骰子A 相同,则骰子B 上的两点的排列方向必定与图中所示的呈对称相反。所以骰子A 和骰子B 不是相同的。如果骰子C 和骰子A 相同,则骰子C 上的三点的排列方向必定与图中所示的呈对称相反。所以骰子A 和骰子C 是不相同的。如果骰子C 和骰子B 相同,则骰子C 上的六点应该是像图中所示的排列方向。由于题目中指明有两只骰子相同,因此相同的必定是骰子B 和骰子C。与它们不同的便是骰子A 了。 12.科拉之死根据安娜和贝思的供词的真伪,可以把科拉的死因列表如下:安娜的供词贝思的供词真被贝思所杀害或自杀或意外事故被谋杀或自杀伪被谋杀但非贝思所为意外事故由于无论这两位女士的供词是真是假,**的两个假定覆盖了一切可能的情况,又由于两个假定不能同时适用,所以只有一个假定是适用的。假定(1)不能适用,因为如果这个假定能适用,则贝思的供词就不是实话。所以只有假定(2)是适用的。既然假定(2)是适用的,那贝思的供词就不能是虚假的,所以只有安娜的供词是虚假的。于是,科拉必定是死于被谋杀。 13.兰瑟先生的坐位根据(3)和(4),围绕桌子的坐位安排只可能是下面两种情况中的一种(M 代表男士,W 代表女士):根据(2),有一位女士坐在坐位a。再根据(1)和(2),一部分坐位的安排为下面两图之一:从根据(3)和(4)推断出的坐位安排可以判定,在Ⅰ中g 和h 必定是男士的坐位。同样,在Ⅱ中h 不能是女士的坐位。因为这样一来,根据(1),一位男士必定坐在坐位b;又根据(3),一位女士必定坐在坐位g;这种情况与从(3)和(4)所得出的坐位安排相矛盾。因此,在Ⅱ中h 和g 必定是男士的坐位。于是,从以上推理并且根据(1),一部分坐位的安排变为下图两者之一:于是,根据只有一位女士坐在两位女士之间(见第一组图形)以及(1)中的要求,完全的坐位安排为下图两者之一:因此,无论是哪一种情况,按(4)的要求,兰瑟先生的坐位总是c。 14.被乘数首位变末位 M 大于1,M×A 小于10,因此,如果A 不是1,则M 和A 是下面两对数字中的一对:(1)2 和4 或 (2)2 和3 以M 和A 的这些数字代入算式,我们寻求F 的值,使得M×F 的末位数为 A。为了寻求适当的F 值,我们还得寻求E 的值,使得M×E 加上进位的数字后末位数为F。如此逐步进行,我们会发现:在(1)的情况下,当M=2 时, D 不会有合适的数值,而当M=4 时,D 或E 不会有合适的数值;在(2)的情况下,当M=2 时,F 不会有合适的数值,但当M=3 时,出现一个合适的乘法算式:上述推理是假定A 不是1。如果A 是1,则M 和F 一个是7 另一个是3。当M 是7 时,E 和F 都是3;但当M 是3 时,则出现一个合适的乘法算式:所以无论哪一种情况,M 都是代表数字3。 15.单 张根据(2),三人手中剩下的牌总共可以配成4 对。再根据(3),洛伊丝和多拉手中的牌加在一起能配成3 对,洛伊丝和罗斯手中的牌加在一起能配成一对,而罗斯和多拉手中的牌加在一起一对也配不成。根据以上的推理,各个对子的分布(A、B、C 和D 各代表一个对子中的一张)如下:洛伊丝手中的牌多拉手中的牌罗斯手中的牌 ABCD ABC D 根据(1)和总共有35 张牌的事实,洛伊丝和罗斯各分到12 张牌,多拉分到11 张牌。因此,在把成对的牌打出之后,多拉手中剩下的牌是奇数,而洛伊丝和罗斯手中剩下的牌是偶数。于是,单张的牌一定是在罗斯的手中。 16.姐妹俩运用(1)和(2),通过反复试验可以发现如下的四种持币情况(H 代表50 美分,Q 代表25 美分,D 代表10 美分,N 代表5 美分): 60 美分75 美分 Ⅰ QQD Ⅲ HNNNNN Ⅱ NNH Ⅳ QDDDDD 于是,根据(3)和(4),辛迪的持币情况必定是Ⅳ。再从(3)和(4),贝齐的持币情况必定是Ⅲ。再从(3)和(4),迪莉娅的持币情况必定是Ⅱ。再从(3)和(4),阿格尼丝的持币情况必定是Ⅰ。因此,在付账之后,各人持有的硬币为:阿格尼丝(Ⅰ)——QQ 贝齐(Ⅲ)——HN 迪莉娅(Ⅱ)——N 辛迪(Ⅳ)——DDD 根据(5),阿格尼丝和贝齐是姐妹俩。 17.第二次联赛根据(1),艾伦、克莱和厄尔各比赛了两场;因此,从(4)得知,他们每人在每一次联赛中至少胜了一场比赛。根据(3)和(4),艾伦在第一次联赛中胜了两场比赛;于是克莱和厄尔第一次联赛中各胜了一场比赛。这样,在第一次联赛中各场比赛的胜负情况如下:艾伦胜巴特艾伦胜厄尔(第四场)克莱胜迪克克莱负厄尔(第三场)根据(2)以及艾伦在第二次联赛中至少胜一场的事实,艾伦必定又打败了厄尔或者又打败了巴克。如果艾伦又打败了厄尔,则厄尔必定又打败了克莱,这与(2)矛盾。所以艾伦不是又打败了厄尔,而是又打败了巴特。这样,在第二次联赛中各场比赛的胜负情况如下:艾伦胜巴特(第一场) 艾伦负厄尔(第二场)克莱负迪克(第四场) 克莱胜厄尔(第三场)在第二次联赛中,只有迪克一场也没有输。因此,根据(4),迪克是第二场比赛的冠军。注:由于输一场即被淘汰,各场比赛的顺序如上面括号内所示。 18.缺失的数字由于B+B 必须进位,而进位的数字充其量是1,所以A 是9,E 是1,F 是0。于是B 必定大于4。如果B 是5,则G 是0 或1,这与不同字母代表不同数字的要求相违背。所以,B 不能是5。如果B 是6,则G 是2 或3;如果B 是7,则G 是4 或5;如果B 是8,则G 是6 或7。这六种可能是:在(1)、(3)、(5)中,C+C 没有进位,所以C 必定小于5。在(2)、(4)、(6)中,C+C 进位1,所以C 必定大于4。这样,上述六种可能可以发展成十五个式子:继续用前面的方法进行推理,可以排除掉十一种可能,从而留下四种可能:因此,无论是哪一种情况,缺失的数字总是3。 19.见习医生的一星期根据(4)和(5),第一位和第二位见习医生在星期四休假;根据(4)和(6),第一位和第三位见习医生在星期日休假。因此,根据(3),第二位见习医生在星期日值班,第三位见习医生在星期四值班。根据(4),第一位见习医生在星期二休假。再根据(3),第二位和第三位见习医生在星期二值班。上述信息可以列表如下(“X”表示值班,“-”表示休假):星期日一二三四五六第一位见习医生- - - 第二位见习医生X X - 第三位见习医生- X X 根据(2),第二位见习医生在星期一休假,第三位见习医生在星期三休假。根据(5),第二位见习医生在星期六休假。因此,根据(1),三位见习医生在星期五同时值班。一星期中其余三天的安排,可以按下述推理来完成。根据(2),第三位见习医生在星期六休假。根据(3),第一位见习医生在星期一、星期三和星期六值班;第二位见习医生在星期三值班;第三位见习医生在星期一值班。 20.电影主角根据陈述中的假设,(1)和(2)中只有一个能适用于实际情况。同样,(3)和(4),(5)和(6),也是两个陈述中只有一个能适用于实际情况。根据陈述中的结论,(1)和(5)不可能都适用于实际情况。同样,(2)和(3),(4)和(6),也是两个陈述不可能都适用于实际情况。因此,要么(1)、(3)和(6)组合在一起适用于实际情况,要么(2)、(4)和(5)组合在一起适用于实际情况。如果(1)、(3)和(6)适用于实际情况,则根据这些陈述的结论,导演是费伊,一位布莱克家的女歌唱家。于是,根据陈述中的假设,任电影主角的是埃兹拉,一位布莱克家的男歌唱家。如果(2)、(4)和(5)适用于实际情况,则根据陈述中的结论,导演是亚历克斯,一位怀特家的男舞蹈家。于是,根据陈述中的假设,任电影主角的是埃兹拉,一位布莱克家的男歌唱家。因此,无论是那一种情况,任电影主角的是埃兹拉。 21.鼓 手四位音乐家的坐位安排,有以下六种可能(A 代表阿琳,B 代表伯顿,C 代表谢里尔,D 代表唐纳德):根据(1)和(3),可以排除Ⅰ和Ⅱ,而Ⅲ、Ⅳ、Ⅴ和Ⅵ变为:根据(5),可以排除Ⅲ和Ⅳ。再根据(2),Ⅴ和Ⅵ变为:根据(4),可以排除Ⅴ。因此鼓手必定是谢里尔。 22.左邻右舍根据(1),每个人的三嗜好组合必是下列组合之一:(i)咖啡,狗,雪茄(v)咖啡,狗,烟斗(ii)咖啡,猫,烟斗(vi)咖啡,猫,雪茄(iii)茶,狗,烟斗(vii)茶,狗,雪茄(iv)茶,猫,雪茄(viii)茶,猫,烟斗根据(5),可以排除(iii)和(viii)。于是,根据(6),(ii)是某个人的三嗜好组合。接下来,根据(8),(v)和(vi)可以排除。再根据(8),(iv)和(vii)不可能分别是某两人的三嗜好组合;因此(i)必定是某个人的三嗜好组合。然后根据(8),排除(vii);于是余下来的(iv)必定是某个人的三嗜好组合。根据(2)、(3)和(4),住房居中的人符合下列情况之一: Ⅰ.抽烟斗而又养狗, Ⅱ.抽烟斗而又喝茶, Ⅲ.养狗而又喝茶。既然这三人的三嗜好组合分别是(i)、(ii)和(iv),那么住房居中者的三嗜好组合必定是(i)或者(iv),如下所示:( ii ) ( i ) ( iv ) ( ii ) ( iv ) ( i )咖啡咖啡茶咖啡茶咖啡猫狗猫或猫猫狗烟斗雪茄雪茄烟斗雪茄雪茄根据(7),(iv)不可能是住房居中者的三嗜好组合;因此,根据(4),卡尔文的住房居中。 23.三个城市如上图所示,对于(3)中所指的两个城市,以X 代表其长方形城区一条边界上的街段数目,以Y 代表另一条边界上的街段数目。于是整个边界的街段数目等于 X+Y+X+Y,即2X+2Y 而市内街段的数目等于 X(Y-1)+Y(X-1),即(XY-X)+(XY-Y)根据(3),对于两个城市而言 2X+2Y=XY-X+XY-Y 解出X, X=3Y/(2Y-3),解出Y, Y=3X/(2X-3)。这表明X 和Y 都得大于1。依次设Y 为2、3、4、5、6 和7,得出下列数值: Y X 2 6 3 3 4 12 5 5 15 7 6 2 7 21 11 既然X 必须大于1,而且根据(1)必须是整数,那么除了上列中的整数之外,X 再也没有别的整数值了。根据(1)和上列数值,这两个城市沿一侧边界的街段数目都是2、3 或 6。根据(2),沿北部边界,阿灵顿有3 个街段,布明汉有6 个街段,坎顿韦尔有9 个街段。由于沿北部边界有9 个街段的城市,不可能满足表示条件(3)的方程,所以坎顿韦尔就是那个市内街段数目不等于沿边界街段数目的城市。总而言之,阿灵顿的沿边界街段和市内街段的数目都是12,而布明汉的这两个数目都是16。 24.骰子面的方位在每只骰子的多面图上,填入题图中显示的点数:然后,依据相对两面点数之和为7 的事实,得出:在每个图形中都有2、5 和6,通过翻动骰子可以显示出三只骰子的相应各面,如下图:现在看得很清楚,骰子A 的面的方位不同于骰子B 和C。所以骰子A 与其他两只不同。 25.需要找零根据(2),阿莫斯有三枚25 美分的硬币。因此,根据(1),他持有的硬币是下列三种情况之一(Q 代表 25 美分,D 代表 10 美分,N 代表5 美分): QQQDDN,QQQDNNN,或QQQNNNNN 于是,根据(1),每个人的硬币枚数只可能是六枚、七枚或者八枚。反复试验表明,用只包括两枚25 美分硬币的六枚硬币组成1 美元,和用只包括一枚 25 美分硬币的八枚硬币组成1 美元都是不可能的。因此,每人身上都带有七枚硬币。各种不同的组合如下(H 代表50 美分):六枚硬币七枚硬币八枚硬币 QQQDDN QQQDNNN QQQNNNNN QQ???? QQDDDDD QQDDDDNN QHDNNN QHNNNNN Q??????? HDDDDD HDDDDNN HDDDNNNN 然后根据(3),每份账单的款额(以美分为单位)是以下各数之一:5, 10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90, 95,100。依次假定每份账单的款额为上列各数,我们发现:除了款额为5、 15、85 或95 美分之外,四人都能不用找零。如果款额为5、15、85 或95 美分,唯独是有两枚25 美分硬币的伯特需要找零。因此,伯特需要找零。 26.谁是医生根据(2),在五人之中有医生的一个孩子,所以除了女儿的儿子,其他人都可能是医生。同样是根据(2),在五人之中有病人的一位父亲或母亲,所以病人要么是女儿,要么是女儿的儿子。根据(3a),如果布兰克先生或者他的夫人是医生,那么他的女儿就不是病人;同时,如果他的女儿或者他女儿的丈夫是医生,他女儿的儿子就不是病人。因此,医生与病人的配对必定是下列情况之一:医生病人(A)布兰克先生他女儿的儿子(B)他的夫人他女儿的儿子(C)他的女儿他的女儿(D)他女儿的丈夫他的女儿根据(1),可排除情况(C)。情况(A)和(B)中,医生的孩子就是布兰克先生的女儿;但是根据(2),病人父母亲中年龄较大的那一位也是布兰克先生的女儿。这种情况与(3b)发生矛盾,因此情况(A)和(B)也可排除。(D)必定是实际的情况,也就是说,医生是布兰克先生女儿的丈夫。这也符合(2)和(3b)的要求,即医生的孩子和病人父母亲中年龄较大的那一位都是男性,但不是同一个人。 27.乘积首位变末位从题目中可以看出,M 不可能是0 或 1,而且 M×B 小于10;A 大于M,故M 不可能是9,而且A 必定大于2。因此,M、A、B 和F 的值必然是下列各种组合之一: a b c d e f g h i j k l m n o p q r M 8 7 7 6 6 6 5 5 5 5 4 4 4 4 4 3 3 3 3 3 3 2 2 2 2 2 2 2 A 9 8 9 7 8 9 6 7 8 9 5 6 7 8 9 4 5 6 7 8 9 3 4 5 6 7 8 9 B 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 2 2 2 3 1 2 2 3 3 4 4 F 2 6 3 2 8 4 0 5 0 5 0 4 8 2 6 2 5 8 1 4 7 6 8 0 2 4 6 8 上表中未标明字母者,是由于有重复数值而应加以排除。为了得出哪一组数值可以产生其余字母所代表的唯一数值,可采用以下方法。计算M×A 得F。类似地,再计算M×F,可能要加上进位的数字,得到E。如此类推。一旦出现某一字母的值不唯一的情况,便把该组排除。结果,只留下j 组,即所以,M 代表的数字是4。 28.健身俱乐部根据(1a)和(2a),利兹第一次去健身俱乐部的日子必定是以下二者之一:(A)肯第一次去健身俱乐部那天的第二天。(B)肯第一次去健身俱乐部那天前六天。如果(A)是实际情况,那么根据(1b)和(2b),肯和利兹第二次去健身俱乐部便是在同一天,而且在20 天后又是同一天去健身俱乐部。根据(3),他们再次都去健身俱乐部的那天必须是在二月份。可是,肯和利兹第一次去健身俱乐部的日子最晚也只能分别是一月份的第六天和第七天;在这种情况下,他们在一月份必定有两次是同一天去健身俱乐部:1 月11 日和1 月31 日。因此(A)不是实际情况,而(B)是实际情况。在情况(B)下,一月份的第一个星期二不能迟于1 月1 日,否则随后的那个星期一将是一月份的第二个星期一。因此,利兹是1 月1 日开始去健身俱乐部的,而肯是1 月7 日开始去的。于是根据(1b)和(2b),他二人在一月份去健身俱乐部的日期分别为:利兹:1 日,5 日,9 日,13 日,17 日,21 日,25 日,29 日;肯:7 日,12 日,17 日,22 日,27 日。因此,根据(3),肯和利兹相遇于1 月17 日。 29.达纳之死分别假定陈述(1)、陈述(2)和陈述(3)为谎言,则达纳的死亡原因如下表:陈述( 1 ) 陈述( 2 ) 陈述( 3 )如果为谎言谋杀,但不是比尔干的被比尔谋杀意外事故这个表显示,没有两个陈述能同时为谎言。因此,要么没有人说谎,要么只有一人说了谎。根据(4),不能只是一个人说谎。因此,没有人说谎。由于没有人说谎,所以既不是谋杀也不是意外事故。因此,达纳死于自杀。注:虽然(4)是真话,但(1)和(2)也都是真话,达纳居然是死于自杀,这似乎有点奇怪。存在这种情况的理由是:当一个陈述中的假设不成立的时候,不论其结论是正确还是错误,这个陈述作为一个整体还是正确的。 30.最后一个划船渡河的人根据(1)和(3),要实现渡河任务,必须采取下述两种方案之一(W 代表女人,M 代表男人,a 代表阿特,b 代表本,c 代表考尔): Ⅰ Ⅱ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ? ? ? ? ? ? ? ? ? ? i M WW M M i M WW M M ii M WW M M ii M WW M M iii M M WW M iii WW M M M iv M M M WW iv WW M M M v M M M WW v M WW M M vi M M M WW vi M M M c a b a c a b a a c b a a c b b a c c b a c c b c ® ® ¬ ¬ ® ® ¬ ¬ ® ® ¬ ¬ a c b c a WW vii M M M WW vii M M M WW ( ) ( ) ? ? ¬ ® 根据(2),在方案Ⅰ的第(v)步中,划船者不能是本也不能是考尔;所以是阿特划的船。于是,根据(2),若采用方案Ⅰ,则是本最后划船渡河。若采用方案Ⅱ,则根据(2),也是本划了最后一次船。因此,无论那一种方案,都是本最后一个划船渡河。在方案Ⅰ和Ⅱ的其余情节是:根据(2),在方案的Ⅱ第(iii)步中,划船者不能是阿特也不能是本,所以是考尔划的船。于是,根据(2),在方案Ⅱ中是本划了第一次船。另外,根据(2),在方案Ⅰ中也是本划了第一次船。 31.倒霉者运用(2)和(3),从反复试验得知,人们围桌而坐的坐位安排必定是下图所示的两种之一(M 代表男士,W 代表女士):根据(1)和(5),安排Ⅱ符合实际情况。接着,根据(4)和(6),巴里和女主人的坐位必定是以下两种情况之一:然后,根据(4)和(7),萨曼莎和倒霉者配偶的坐位必定是以下两种情况之一(曲线指出了夫妻关系):无论哪种情况,纳塔利总是倒霉者。这两种坐位安排的全貌如下图所示: 32.最小的和加法式Ⅰ中的E、Ⅱ中的A 和Ⅲ中的L 都有相同的表现:只有数字5 能有这种表现。例如: 5+3=8, 5+4=9, 5+8=10+3,5+9=10+4。因此得出:用数字替代Ⅰ中的L,Ⅱ中的E,Ⅲ中的A,以相应得出Ⅰ中的A 值,Ⅱ 中的L 值,Ⅲ中的E 值。经过反复试验,得到(已经删去那些从第二列向第三列进位1 从而造成替代结果不能成立的情况):从上述部分的加法算式中可以看出,Ⅰ的和最小。这些加法算式可以进一步补全。在每个算式中,留下来的字母,其数值不能同于已在该式中出现的数值,而且左端的第一个字母不能代表0。这样,可能的加法算式,Ⅰ有四种,Ⅱ有一种,Ⅲ有两种,如下所示: 33.李、戴尔、特里和马里恩运用(2)中的信息,可以进行如下的推理。李的母亲和马里恩的女儿或者是同一个人,或者不是同一个人。在情况Ⅰ下,戴尔的哥哥不是李就是马里恩①。因此,特里是李的母亲、马里恩的女儿,而特里的父亲不是马里恩就是戴尔。但特里的父亲不能是戴尔,因为戴尔的哥哥不是李就是马里恩。这样,特里的父亲就是马里恩。现在假设戴尔的哥哥是李,于是根据(1),戴尔是男性,这与(3)矛盾。所以戴尔的哥哥是马里恩。根据(3),戴尔和李都是女性。因此,在情况Ⅰ下,马里恩是唯一的男性。在情况Ⅱ下,根据(1),戴尔的哥哥与特里的父亲必定是同一个人,是唯一的男性。所以,马里恩必定是特里的父亲、戴尔的哥哥,而这意味着马里恩是情况Ⅱ下唯一的男性。因此,无论怎么说,马里恩是唯一的男性。 ①如果戴尔的哥哥既不是李也不是马里恩,那么他必定是特里,从而戴尔就是马里恩的女儿、李的母亲。根据(1),马里恩与李必定同性别,但这与(3)矛盾。——译者注 34.圈出的款额运用(2)和(3),经过反复试验,可以发现,只有四对硬币组能满足这样的要求:一对中的两组硬币各为四枚,总价值相等,但彼此间没有一枚硬币面值相同。各对中每组硬币的总价值分别为:40 美分、80 美分、125 美分和130 美分。具体情况如下(S 代表1 美元,H 代表 50 美分,Q 代表 25 美分, D 代表 10 美分, N 代表5 美分的硬币): DDDD DDDH QQQH DDDS QNNN QNQQ NDDS QNHH 运用(1)和(4),可以看出,只有30 美分和100 美分能够分别从两对硬币组中付出而不用找零。但是,在标价单中没有100。因此,圈出的款额必定是30。 35.谁是教授根据(2),在坐位a、d 和e 中,只有一个是男士的坐位。于是根据(2)和(5),一部分的坐位安排有三种方案(M 代表男士,W 代表女士):在方案Ⅰ中,根据(3),卡丽的丈夫坐在坐位 b、c、i 或 j 上。但是根据(5),卡丽的丈夫不可能是唯一坐在两位女士之间的男士。因此,方案Ⅰ可以排除。在方案Ⅱ中,一位男士已经坐在两位女士之间的坐位 f 上。因此,根据(3),他必定是卡丽的丈夫。接着,为了保证卡丽的丈夫是唯一坐在两个女士之间的男士,坐位i 上必须是位男士。可是这样一来,根据(5),一位女士一定要坐在坐位c 上,而这与(4)发生矛盾。因此,方案Ⅱ也可以排除。这样,Ⅲ便是正确的方案。在Ⅲ中,根据(2)和(3),坐位c 上坐的必定是一位男士;从而根据(5),坐位i 上坐的是一位女士。根据(4),坐在坐位j 上的不能是女士;因此,是一位男士坐在坐位j 上,而根据(3),这个人是卡丽的丈夫。最后,根据(5),坐在坐位b 上的是一位女士。这样,坐位安排的情况变成:测试你的逻辑推理能力然后,根据(2),比拉的丈夫坐在坐位d。接着,根据(1)和(5),阿米莉亚的丈夫坐在坐位h,丹尼斯的妻子坐在坐位i。再根据(5),埃尔伍德的妻子坐在坐位a。于是,根据(6),卡丽是教授。概括起来,完整的坐位安排如下: 36.三个J (i)由于A、D 和G 代表的是0 以外的三个不同的数字,所以J 必定是 6、7、8 或9。(ii)由于C、F、I 代表三个不同的数字,所以它们的和不会超过24;而为了保证J 是6、7、8 或9,它们的和不能超过19。(iii)如果任何两列的每列数字之和为6、7、8 或9,则余下一列的和也必定是6、7、8 或9;可是,从A 到I 的各个字母代表的是9 个不同的数字,不可能出现这种情况。因此,最多只能有一列的和为6、7、8 或9。从以上三点可以得出如下的结论:(a)如果 A+D+G=6,则C+F+I 必定是 16、7 或 17。(b)如果 A+D+G=7,则 C+F+I 必定是17、8 或 18。(c)如果A+D+G=8,则C+F+I 必定是 18、9 或 19。(d)如果 A+D+G=9,则 C+F+I 必定是 19。从(a)、(b)、(c)、(d)可以推导出B+E+H 的和,一共有十种可能: A+D+G B+E+H C+F+I J Ⅰ 6 5 16 6 Ⅱ 6 17 7 7 Ⅲ 6 16 17 7 Ⅳ 7 6 17 7 Ⅴ 7 18 8 8 Ⅵ 7 17 18 8 Ⅶ 8 7 18 8 Ⅷ 8 19 9 9 Ⅸ 8 18 19 9 Ⅹ 9 8 19 9 在上面的十种情况中,只有Ⅷ和Ⅹ中四栏的总和为 45,与 0~9 这十个数字之和相等。因此,J 必定代表9。进一步的验证表明,存在以下几种可能的组合: A+D+G B+E+H C+F+I Ⅷ 1+3+4 5+6+8 0+2+7 1+2+5 4+7+8 0+3+6 Ⅹ 2+3+4 0+1+7 5+6+8 1+3+5 0+2+6 4+7+8 1+2+6 0+3+5 4+7+8 37.谁没有输过根据(1),以下三种情况必有其一(A 和B 各代表一个对子中的一张牌, S 代表单张):多丽丝手中劳拉手中雷内手中 Ⅰ A AB BS Ⅱ A BS AB Ⅲ S AB AB 然后,根据(2)、(3)和(4),抽牌只能按下列某一过程进行:但是,过程Ⅰ、Ⅱa 和Ⅱb 不能满足(4),因此加以排除。根据(5),过程Ⅱc 必定在某一盘中出现,而过程Ⅲ必定在另一盘中出现。于是,多丽丝和雷内手中都剩下过单张。因此,只有劳拉手中没有剩下过单张,她没有输过。 38.谁是凶手根据陈述中的假设,(1)和(2)中只有一个能适用于实际情况。同样,(3)和(4),(5)和(6),也是两个陈述中只有一个能适用于实际情况。根据陈述中的结论,(2)和(5)不可能都适用于实际情况。因此,能适用于实际情况的陈述组合是下列组合中的一组或几组:(A)(1)、(4)和(5);(B)(1)、(3)和(5);(C)(1)、(4)和(6);(D)(1)、(3)和(6);(E)(2)、(4)和(6);(F)(2)、(3)和(6)。如果(A)能适用于实际情况,则根据(1)的结论,凶手是男性;根据(4)的结论,受害者是女性;可是根据(5)的假设,凶手与受害者性别相同。因此(A)不适用。如果(B)能适用于实际情况,则根据有关的假设,凶手与受害者有亲缘关系而且职业相同、性别相同。这与各个家庭的组成情况有矛盾,因此(B)不适用。如果(C)能适用于实际情况,则根据有关的结论,凶手是男性,受害者是个女性医生。接着根据(1)和(4)的假设,凶手是律师,凶手与受害者有亲缘关系。这与各个家庭的组成情况有矛盾,因此(C)不适用。如果(D)能适用于实际情况,则根据(1)的结论,凶手是男性;根据(3)的结论,受害者也是男性;可是根据(6)的假设,凶手与受害者性别不同。因此(D)不适用。如果(E)能适用于实际情况,则根据(2)的结论,凶手是医生;根据(6)的结论,受害者也是医生;可是根据(4)的假设,凶手与受害者职业不同。因此(E)不适用。因此只有(F)能适用于实际情况。根据有关的结论,凶手是医生,受害者是男性医生。于是根据(6)的假设,凶手是女性。接着,根据各个家庭的组成情况,凶手必定是贝蒂。(2)的假设则表明,受害者是杜安;而且,(3)的假设和(2)、(6)的结论相符合。 39.没有出黑桃总共玩了四圈牌;因此,根据(4)和(5),必定在某一圈先手出的牌是王牌而且这圈是先手胜。于是,根据(2)和(3),先手和胜方的序列是以下二者之一: I II X 先手,胜X 先手Y 胜 X 先手Y 胜Y 先手,胜 Y 先手,胜X 胜Y 先手 X 胜Y 先手X 先手,胜不是先出牌而能取胜,表明他或她打的是一张王牌。因此,无论是Ⅰ或 Ⅱ,都要求一方有两张王牌,而另一方有一张王牌。从而根据(1),黑桃是王牌。假定Ⅰ是符合实际情况的序列,则根据(1)和(5)以及第一圈时Y 手中必定有一张黑桃的事实,X 在第一圈时不是先出了王牌黑桃而取胜的;根据(1)和(5)以及X 在第四圈时必定要出黑桃的事实,Y 在第三圈时也不是先出了黑桃而取胜的。这同我们开始时分析所得的结论矛盾。所以Ⅱ是符合实际情况的序列。这样,根据(1)和(5)以及第二圈时 X 手中必定有一张黑桃的事实,Y 在第二圈时不是先出了黑桃而取胜的。因此在第四圈时,X 先出了黑桃并以之取胜。根据上述推理,在第一、三、四圈都出了黑桃。因此,在第二圈中没有出黑桃。其他的情况是:X 在第一圈时先出的是Y 手中所没有的花色。既然X 手中应该有两张黑桃,那么根据(1),X 是男方,他在第一圈先出的是梅花。再根据(1),男方接着在第二圈时出了红心。因此,根据(1)和(5),女方在第二圈时先出了方块并以之取胜;根据(4),她在第三圈时先出了红心;而根据(1),她在第四圈时出的是方块。 40.勒索者运用(3)和(4),经过反复试验,可得出人们围桌而坐的各种可能的坐位安排(M 代表男士,W 代表女士):接着,根据(2)和(6),Ⅱ和Ⅳ可排除,从而得到一部分坐位的安排情况如下:接着,根据(1)和(5),Ⅰ可排除,这样部分坐位的安排情况必定如下(每条曲线连接着一对夫妇):最后,根据(7),布莱尔必定是勒索者的配偶;因此布兰奇是勒索者。全部的坐位安排如下图: 41.没有放上的数字根据(1),(A+B+C+D)+(D+E+F+G)+(G+H+I+A) =14+14+14,即 2A+2D+2G+B+C+E+F+H+I=42 0~9 这十个数字之和为45;因此,如果以J 代表没有放上的数字,则 A+B+C+D+E+F+G+H+I=45-J。从第一个方程中减去第二个方程,得到: A+D+G=J-3。由于A+D+G 至少等于3,而J 最多等于9,只可能有以下的情况: A+D+G J (i) 3 6 (ii) 4 7 (iii) 5 8 (iv) 6 9 于是,以下情况中必然有一种会发生:从而得到:由此可见,只有(i)和(ii)能继续补上数字而不致发生重复,即:因此,根据(2),6 和7 分别是两个三角形中没被放上的数字。 42.指认罪犯根据(1),高个男人必定站成下列形式之一(t 代表高个男人): tttt 或ttt-或-ttt 或-tt- 根据(2),白皙男人必定站成下列形式之一(f 代表白皙男人): ff--或--ff 或 f-ff 或 ff-f 根据(3),消瘦男人必定站成下列形式之一(s 代表消瘦男人): s--s 或s-s-或-s-s 或-s--或--s- 根据(4),漂亮男人必定站成下列形式之一(g 代表漂亮男人): g---或---g 根据(5),并根据(1),上述特征中的一部分可以给这四个男人分派如下:第一个男人第二个男人第三个男人第四个男人白皙消瘦高个漂亮高个接着,根据(2),部分特征的分布必定是下列三种情况之一:第一个男人第二个男人第三个男人第四个男人 Ⅰ 白皙消瘦高个漂亮高个白皙 Ⅱ 白皙消瘦高个漂亮高个白皙白皙 Ⅲ 白皙消瘦高个漂亮高个白皙白皙然后,根据(3)和(6),只有在Ⅰ和Ⅲ中,第四个男人可能还是消瘦的;而且在Ⅰ、Ⅱ和Ⅲ中,不会再有其他男人是消瘦的。再根据(1)和(6),只有在Ⅰ中,第四个男人可能还是高个子,而且只有当第四个男人不是消瘦的时候这种情况才能发生;而且在Ⅰ、Ⅱ和Ⅲ中,不会再有其他男人是高个子。此外,根据(4),不会再有其他男人是漂亮的。因此,完整的特征分布必定是下列情况之一:第一个男人第二个男人第三个男人第四个男人 Ⅰ a 白皙消瘦高个漂亮高个白皙 Ⅰ b 白皙消瘦高个漂亮高个消瘦白皙 Ⅰ c 白皙消瘦高个漂亮高个高个白皙 Ⅱ 白皙消瘦高个漂亮高个白皙白皙 Ⅲ a 白皙消瘦高个漂亮高个白皙白皙 Ⅲ b 白皙消瘦高个漂亮高个白皙白皙消瘦根据(7),可排除Ⅰa、Ⅰb、Ⅰc 和Ⅱ。Ⅲa 和Ⅲb 显示:目击者指认第一个男人是罪犯。 43.最后一个划船过湖的人八个人用只能乘坐三人的小船过湖,需要向湖对岸摆渡四次。根据(5),总有一次向湖对岸摆渡时船上只有两个人。根据(2)、(3)和(5),总有一个男人留在原地,直到最后一次摆渡(在整个过程中不一定是同一个男人)。根据以上的推断并根据(1)、(4)和(5),头四次摆渡采用的是下列两种方式中的一种(W 代表女人,M 代表男人,a 代表亚伯拉罕,b 代表巴雷特,c 代表克林顿,d 代表道格拉斯): I i M WWWW M M M ii M WWWW M M M a a b d c b a d ( ) ( ) ® ¬ ( ) ( ) ( ) ( ) ( ) ( ) iii M WW M WW M M iv M WW M M M WW II i M M WWWW M M ii M M WWWW M M iii M WWWW M M W M iv M WWW M M M W b c a d b d a c c d a b c d b a b c d a b d a c ® ¬ ® ¬ ® ¬ 然后,根据(2)、(3)和(5),第(v) 步是巴雷特带着两个女人划船过湖;由于这种情况只能在方式Ⅰ中出现,所以可排除方式Ⅱ。接着,根据(2)(3)和(5),第(vi) 步是亚伯拉罕或克林顿划船返回而且船上只有一个人;最后,第(vii)步,是道格拉斯带着亚伯拉罕或克林顿划向湖对岸。 44.第六号纸牌假设第六号纸牌是一张A。(a)于是,根据(5),第七号和第八号纸牌都不能是A;根据(4),它们不能是Q;根据(2),它们也不能是K。(b)另外,根据(3), 在第七号和第八号纸牌中最多只能有一张是J。因此,根据(6), 第六号纸牌不可能是A。假设第六号纸牌是一张Q。(a)于是, 根据(5),第四、五、七、八号纸牌都不能是Q; 而且根据(4),它们也不能是A。(b)另外,根据(6),第一、二、三号纸牌将是两张A 和一张 Q;可是根据(4)和(5),这是不可能的。因此,根据(6),第六号纸牌不可能是Q。假设第六号纸牌是一张J。(a)于是,根据(1),第七号和第八号纸牌都不能是A;根据(5),它们不能是J;根据(2),它们也不能是K。(b)另外,根据(2),在第七号和第八号纸牌中最多只能有一张是Q。因此,根据(6),第六号纸牌不可能是J。于是,第六号纸牌只能是K。可以确定的纸牌是第一号至第六号。由于第六号纸牌是K,根据(2)和(3),第五号或第四号纸牌是Q。如果第五号纸牌是Q,那么根据(3),第三号纸牌J。再根据(2),第二号纸牌不能是Q,而第一号和第四号纸牌则分别是 K 和Q。再根据(6),第二号纸牌必定是J,而这与(5)发生矛盾。因此,第五号纸牌不是 Q,而第四号纸牌是 Q。于是,根据(5),第一号和第三号纸牌都不是 Q;根据(3),第七号和第八号纸牌也都不是 Q;而根据前面的推断,第五号纸牌也不是Q。因此,第二号纸牌是Q。接着,根据(3),第三号纸牌是J;根据(2),第一号纸牌是K。随后根据(5)和(6),第五号纸牌是A。余下第七号和第八号纸牌,则分别是J 和A 或A 和J。 45.最短的时间根据(2),各人汽艇在静水中每小时行驶的英里①数,等于各人帐篷至奥斯本帐篷的距离的英里数。设d 为这个距离(单位为英里),r 为各艘汽艇的在静水中的速度(单位为英里/小时),t 为返程所花的时间(单位为小时)。根据(3),设c 为水流的速度(单位为英里/小时)。逆流而上时, d/ (r-c)=r/(r-c)=t;顺流而下时,d/(r+c)=r/(r+c)=t。于是,根据(1)和(4),各人去程和返程所用的时间如下表:去程所用时间(小时) 返程所用时间(小时)威尔逊r/(r-c)=5/4 r/(r+c)=t 泽维尔r/(r-c)= 7/6 r/(r+c)= t 约曼r/(r+c)=5/6 r/(r-c)=t 曾格r/(r+c)= 3/4 r/(r-c)= t 其中,r 和t 是因人而异,而c 则对各人都一样。对于威尔逊, r=5 c, t=5/6,即 50 分钟。对于泽维尔,r = , = ,即分钟。对于约曼, = , = ,即7c t 7 / 8 52 r 5C t 5 / 4 1 2 75 分钟。对于曾格, r=3c, t=3/2,即90 分钟。所以各人花在往返旅程上的全部时间,威尔逊是125 分钟,泽维尔是 122 1 2 125 135 分钟,约曼是分钟,曾格是分钟。因此,泽维尔的全程时间最短。结果,由于约曼帐篷同奥斯本帐篷的距离为5c,而曾格帐篷同奥斯本帐篷的距离为3c,所以在上游约曼的帐篷比曾格的帐篷更远。由于在下游泽维尔帐篷同奥斯本帐篷的距离是7c,而威尔逊是5c,因此——也许令人惊讶— —泽维尔的帐篷最远。 46.仁爱的人每个人都恰好有三个特点。因此,根据(1)和(2),亚当具有下列四组特点中的一组:诙谐,漂亮,强壮诙谐,漂亮,仁爱漂亮,强壮,仁爱强壮,聪明,仁爱根据(1)和(3),布拉德具有下列四组特点的一组:诙谐,聪明,漂亮聪明,漂亮,强壮聪明,漂亮,仁爱漂亮,强壮,仁爱根据(1)和(4),科尔具有下列四组特点的一组:漂亮,强壮,聪明漂亮,强壮,仁爱强壮,聪明,仁爱聪明,诙谐,仁爱根据上面的特点组合并且根据(1),如果亚当具有仁爱的特点,那么布拉德和科尔都是聪明而又漂亮的,亚当就不能是聪明或漂亮的了。这种情况不可能,因此亚当不具有仁爱的特点。根据上面的特点组合并且根据(1),如果布拉德具有仁爱的特点,那么亚当和科尔都是漂亮的,布拉德就不能具有漂亮的特点了。这种情况不可能,因此布拉德不具有仁爱的特点。于是,科尔必定是具有仁爱特点的人了。我们还可以看出其中一人的全部三个特点,以及另外两个人各有的两个特点。由于科尔是仁爱的,所以亚当是诙谐、漂亮和强壮的;布拉德是既漂亮又聪明;从而科尔不能是漂亮的,所以科尔是既聪明又仁爱的人。 47.“老处女” 根据(1),必然是以下情况(A、B 和C 各代表一对中的一张,M 代表“老处女”):多萝西手中洛雷塔手中罗莎琳手中 A BC ABCM 然后,根据(2)、(3)和(4), 抽牌只能按下列某一过程进行:根据(4),过程(a)、(b)、(c)、(d)不能完成,因此都加以排除。根据(5),可排除过程(e)。因此过程(f)是实际进行的过程,是多萝西手中留下了“老处女”。 48.史密斯家的人根据(1),奥德丽做健美操的日子,不是星期日和星期五,便是星期一和星期六。 Ⅰ.如果奥德丽在星期日和星期五做健美操,那么根据(2)和(5),布伦达在星期二和星期六做健美操。 Ⅱ.如果奥德丽在星期一和星期六做健美操,那么根据(2)和(5), 布伦达在星期日和星期四做健美操。如果Ⅰ能适用于实际情况,则根据(5),康拉德和丹尼尔做健美操的日子是星期一、星期三和星期四;根据(3)和(4),具体在哪一天,可以是 Ⅰa.康拉德在星期一和星期四做健美操,丹尼尔在星期三做健美操,或者 Ⅱb.丹尼尔在星期一和星期三做健美操,康拉德在星期四做健美操。如果Ⅱ能适用于实际情况,则根据(5),康拉德和丹尼尔做健美操的日子是星期二、星期三和星期五;根据(3)和(4),具体在哪一天,可以是 Ⅱa.康拉德在星期二和星期五做健美操,丹尼尔在星期三做健美操,或者 Ⅱb.丹尼尔在星期三和星期五做健美操,康拉德在星期二做健美操。上述结果可以列表如下:奥德丽布伦德康拉德丹尼尔 Ⅰa 星期日、五星期二、六星期一、四星期三 Ⅰb 星期日、五星期二、六星期四星期一、三 Ⅱa 星期一、六星期日、四星期二、五星期三 Ⅱb 星期一、六星期日、四星期二星期三、五根据(3)和(5),在Ⅰb 和Ⅱb 中,康拉德没有另一个日子可做健美操。根据(4)和(5),在Ⅰa 中, 丹尼尔可在星期五做健美操;在Ⅱa 中,丹尼尔可在星期一做健美操。在这两种情况中,史密斯家的成员总是奥德丽和丹尼尔。 49.应聘在以下各表中,A 代表奥尔登,B 代表布伦特,C 代表克雷格,D 代表德里克,g 代表高中学历,w 代表至少两年的工作经验,v 代表退伍军人,r 代表有符合要求的证明书,X 代表满足要求,O 代表不满足要求。下表是运用(4)和(5)得到的结果。 A B C D g w v X X r X 接着,根据(2)和(3),得到下列填好了一部分的四张表。 Ⅰ Ⅱ A B C D A B C D g X X g X X w X X w O O v X X v X X r X r X Ⅲ Ⅳ A B C D A B C D g O O g O O w X X w O O v X X v X X r X r X 在Ⅳ中,没人能同时满足g 和w 这两项要求; 所以根据(1),把表Ⅳ 排除。根据(1),可在表Ⅰ、Ⅱ和Ⅲ中填上一些O,从而得到: Ⅰ Ⅱ Ⅲ A B C D A B C D A B C D g X X O g X X g O O w O X X w O O w O X X v O X X O v O X X v X X O r O X r X r O X 还是根据(1),在表Ⅰ、Ⅱ和Ⅲ中,都可以各填上一个X,从而得到: Ⅰ Ⅱ Ⅲ A B C D A B C D A B C D g X X O g X X g O O X w O X X w X O O w O X X v O X X O v O X X v X X O r X O X r X r O X 还是根据(1),在表Ⅰ、Ⅱ和Ⅲ中,都可以各填上一些O,从而得到: Ⅰ Ⅱ Ⅲ A B C D A B C D A B C D g X X O O g X X O g O O O X w O X X w O X O O w O X X v O X X O v O X X v X X O r O X O X r X r O X 根据(1),由于在表Ⅲ中没人能同时满足g 和v 这两项要求,所以把表 Ⅲ排除。至此,已可看出,只有布伦特能比其他三人满足更多的要求,所以被雇用的是布伦特。要完成表Ⅰ和Ⅱ,可根据(1)各填上一些X,从而得到: Ⅰ Ⅱ A B C D A B C D g X X O O g X X O w X O X X w O X O O v O X X O v O X X r O X O X r X X 只要再填上一些O,表Ⅱ即可完成。 50.罪恶累累根据(1), 谋杀犯的坐法当如以下二者之一(m 代表谋杀犯):根据(2), 勒索犯的坐法当如以下二者之一(e 代表勒索犯):根据(3), 诈骗犯的坐法当如以下三者之一(s 代表诈骗犯):根据(4),盗窃犯的坐法当如以下四者之一(t 代表盗窃犯):根据(5), 如果有一个人犯了所有这四种罪,则其他五人每人犯的罪不会超过一种。但是,根据以上的坐法,至少有两个谋杀犯、两个勒索犯、三个诈骗犯、四个盗窃犯围桌而坐。因此,不可能有人犯了所有这四种罪。同样,也不可能有一个人犯了两种罪,而同时其他五人每人只犯一种罪。因此,根据(6),犯罪最多的那个人是犯了三种罪。于是,根据以上的坐法,有一个人犯了三种罪,有三个人每人各犯了两种罪,有两个人每人各犯了一种罪。因此,恰有两个谋杀犯、两个勒索犯、三个诈骗犯和四个盗窃犯。根据(8)和(9),某些犯罪类型可以与具体人物结合如下:根据从(3)导出的可能坐法,并根据(10),情况变成以下二者之一:根据从(4)导出的可能坐法,并根据(5)和(7),可排除情况Ⅰ,而情况Ⅱ变成:根据从(2)导出的可能坐法,并根据(5)和(7),情况Ⅱ变成:根据从(1)导出的可能坐法,并根据(5)和(7),情况Ⅱ变成:因此,布赖斯的妻子所犯罪的数目超过了其他各人。 __