01背包+互斥背包+条件背包。详细见代码：
#include<iostream>
using namespace std;
int n,t,m,s;
int cost[105],hap[105];
int f[105];
int main()
{
while(scanf("%d%d",&n,&t)!=EOF)
{
int i,j,k;
memset(f,-1,sizeof(f));
f[0]=0;
for(k=1;k<=n;k++)
{
scanf("%d%d",&m,&s);
for(i=0;i<m;i++)
scanf("%d%d",&cost[i],&hap[i]);
if(s==0)
{
int d[105];
memset(d,-1,sizeof(d));
for(i=0;i<m;i++)
for(j=t;j>=cost[i];j--)
{
if(d[j-cost[i]]!=-1&&d[j]<d[j-cost[i]]+hap[i])
d[j]=d[j-cost[i]]+hap[i];
if(f[j-cost[i]]!=-1&&d[j]<f[j-cost[i]]+hap[i])
d[j]=f[j-cost[i]]+hap[i];
}
memcpy(f,d,sizeof(d));
}
else if(s==1)
{
for(j=t;j>=0;j--)
{
int temp=-1; //注意:找这m个中的最大值时,应先找到最大值,再更新f[j].不要边比较边更新,如果出现f[j]<f[j-cost[i]]+hap[i]而更新f[j],那么当下次出现f[j]<f[j-cost[i]]+hap[i],并且cost[i]==0时,就会变成f[j]+hap[i],但f[j]已经更新,就会出错.
for(i=0;i<m;i++)
{
if(j-cost[i]>=0&&f[j-cost[i]]!=-1&&temp<f[j-cost[i]]+hap[i])
temp=f[j-cost[i]]+hap[i];
}
f[j]=f[j]>temp?f[j]:temp;
}
}
else if(s==2)
{
for(i=0;i<m;i++)
for(j=t;j>=cost[i];j--)
if(f[j-cost[i]]!=-1&&f[j]<f[j-cost[i]]+hap[i])
f[j]=f[j-cost[i]]+hap[i];
}
}
int ans=-1;
for(i=0;i<=t;i++)
if(ans<f[i]) ans=f[i];
printf("%d\n",ans);
}
return 0;
}posted @
2010-08-18 09:58 wuxu 阅读(328) |
评论 (0) |
编辑 收藏BFS+优先队列+位运算.
#include<iostream>
#include<queue>
using namespace std;
const int inf=0x7fffffff;
int n,l,nop,nw,s,d;
char oper[35][25];
int cost[35];
char beg[22][22],end[22][22];
int hash[1050000];
typedef struct node
{
int cst;
int integ;
bool operator< (node a) const
{
return a.cst<cst;
}
}Node;
void transf(int i,int &tt)
{
int j,k;
for(j=0;j<l;j++)
{
k=l-j-1;
if(oper[i][j]=='N') continue;
else if(oper[i][j]=='F') tt=tt^(1<<k);
else if(oper[i][j]=='S') tt=tt|(1<<k);
else if(oper[i][j]=='C') tt=tt&(~(1<<k));
}
}
void bfs(int v)
{
priority_queue<Node> q;
Node temp;
temp.cst=0;
temp.integ=s;
hash[s]=0;
q.push(temp);
int ans;
bool mark=false;
while(!q.empty())
{
temp=q.top();
q.pop();
if(temp.integ==d)
{
mark=true;
ans=temp.cst;
break;
}
for(int i=1;i<=nop;i++)
{
int tt=temp.integ;
transf(i,tt);
Node tp;
tp.integ=tt;
tp.cst=temp.cst+cost[i];
if(tp.cst<hash[tp.integ])
{
hash[tp.integ]=tp.cst;
q.push(tp);
}
}
}
if(mark)
{
if(v==nw) printf("%d\n",ans);
else printf("%d ",ans);
}
else
{
if(v==nw) printf("NP\n");
else printf("NP ");
}
}
int main()
{
int i,v;
scanf("%d",&n);
while(n--)
{
scanf("%d%d%d",&l,&nop,&nw);
for(i=1;i<=nop;i++)
scanf("%s%d",oper[i],&cost[i]);
for(i=1;i<=nw;i++)
scanf("%s%s",beg[i],end[i]);
for(v=1;v<=nw;v++)
{
for(i=0;i<(1<<l);i++) hash[i]=inf;
s=d=0;
for(i=0;i<l;i++)
s+=(beg[v][i]-48)*(1<<(l-i-1));
for(i=0;i<l;i++)
d+=(end[v][i]-48)*(1<<(l-i-1));
bfs(v);
}
}
return 0;
}
posted @
2010-08-17 17:22 wuxu 阅读(169) |
评论 (0) |
编辑 收藏
状态压缩DP（三进制压缩）。
由于第i行的放置受到第i-1和i-2行放置情况的影响。我们用0表示方格(i-1,j)和(i-2,j)未放置炮兵；1表示方格(i-1,j)未放炮兵，方格(i-2,j)已被放上炮兵；2表示方格(i-1,j)被放上了炮兵。那么第i-1行和i-2行的放置情况可以用m位的三进制表示。如果放置情况为0,对应的第i行才可以放炮兵，为1和2都不能放。
f[i][j]表示前i行放置好后,并且放置情况为j时炮兵的最大数量。详细见代码：
#include<iostream>
using namespace std;
int n,m;
int map[105][15];
int f[2][60000];
int b[15],s[15];
void dfs(int i,int j,int cur,int sta,int num)
{
if(cur>m)
{
if(f[i&1][sta]<f[(i-1)&1][j]+num)
f[i&1][sta]=f[(i-1)&1][j]+num;
return;
}
int t,d;
if(s[cur]>0) t=s[cur]-1;
else t=0;
d=sta+t*b[cur-1];
dfs(i,j,cur+1,d,num);
if(map[i][cur]=='P'&&s[cur]==0)
{
d=sta+2*b[cur-1];
if(cur+1<=m)
{
if(s[cur+1]>0) t=s[cur+1]-1;
else t=0;
d+=t*b[cur];
}
if(cur+2<=m)
{
if(s[cur+2]>0) t=s[cur+2]-1;
else t=0;
d+=t*b[cur+1];
}
dfs(i,j,cur+3,d,num+1);
}
}
int main()
{
int i,j,k;
b[0]=1;
for(i=1;i<=10;i++) b[i]=b[i-1]*3;
while(scanf("%d%d",&n,&m)!=EOF)
{
for(i=1;i<=n;i++)
{
getchar();
for(j=1;j<=m;j++)
scanf("%c",&map[i][j]);
}
memset(f,-1,sizeof(f));
f[0][0]=0;
for(i=1;i<=n;i++)
{
for(j=0;j<b[m];j++) f[i&1][j]=-1;
for(j=0;j<b[m];j++)
{
if(f[(i-1)&1][j]!=-1)
{
s[0]=1;
int v=j;
for(k=1;k<=m;k++)
{
s[k]=v%3;
v/=3;
}
dfs(i,j,1,0,0);
}
}
}
int ans=-1;
for(i=0;i<b[m];i++)
if(ans<f[n&1][i]) ans=f[n&1][i];
printf("%d\n",ans);
}
return 0;
}
posted @
2010-08-15 22:08 wuxu 阅读(147) |
评论 (0) |
编辑 收藏
经典的压缩DP.
题目描述:
Bugs公司生产一种2x3单位尺寸的高科技芯片，芯片被嵌入NxM的模板内。模板接受过严格的检查，损坏的单位小方格已被标上黑色记号。
嵌入芯片的要求是，放置芯片的区域内不能有黑色记号，芯片间不能重叠。 求出可能的最大芯片数量。
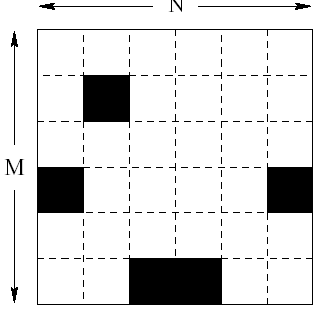
分析：
我们从左至右考虑每列的放置。由于芯片长度只有3，所以第j列芯片的放置只受第j-1和j-2列放置情况的影响。同时，如果方格(i,j-1)被黑色标记或其他芯片占据，方格(i,j-2)即使空闲对第j列也没影响。
这里以0表示方格(i,j-2),(i,j-1)空闲； 以1表示方格(i,j-2)被占据,方格(i,j-1)空闲；以2表示方格(i,j-1)被占据。对于每一行有三种可能的状态。所以第j-2和j-1列的放置情况可以用m位的3进制表示。
状态转移方程推导：
假如我们现在要放置第j列，那么它将受到前两列放置情况的影响。那么我们怎么来表示状态转移呢？
令f[i][j]前j列放置好后，并且放置情况为i时芯片的最大数量。f[i][j]=max{f[k][j-1]+num}. 由此,第j列的放置可由前j-1列的放置情况来推导。
详细见代码：
#include<iostream>
using namespace std;
int n,m,t;
bool bug[12][155];
int f[60000][2];
int b[12],s[12];
void dfs(int j,int i,int cur,int sta,int num)
{
int tt,d;
if(cur>m)
{
if(f[sta][j&1]<f[i][(j-1)&1]+num)
f[sta][j&1]=f[i][(j-1)&1]+num;
return;
}
//当前位置不放芯片.
if(bug[cur][j]) tt=2;
else if(s[cur]>0) tt=s[cur]-1;
else tt=0;
d=sta+tt*b[cur-1];
dfs(j,i,cur+1,d,num);
//横着放芯片.
if(cur+1<=m&&s[cur]==0&&s[cur+1]==0&&!bug[cur][j]&&!bug[cur+1][j])
{
d=sta+2*b[cur-1]+2*b[cur];
dfs(j,i,cur+2,d,num+1);
}
//竖着放芯片.
if(cur+2<=m&&s[cur]<=1&&s[cur+1]<=1&&s[cur+2]<=1&&!bug[cur][j]&&!bug[cur+1][j]&&!bug[cur+2][j])
{
d=sta+2*b[cur-1]+2*b[cur]+2*b[cur+1];
dfs(j,i,cur+3,d,num+1);
}
}
int main()
{
int i,j,k,v;
b[0]=1;
for(i=1;i<=10;i++)
b[i]=b[i-1]*3;
scanf("%d",&t);
while(t--)
{
int x,y;
scanf("%d%d%d",&n,&m,&k);
memset(bug,false,sizeof(bug));
for(i=0;i<k;i++)
{
scanf("%d%d",&x,&y);
bug[y][x]=true;
}
memset(f,-1,sizeof(f));
f[b[m]-1][0]=0;
for(j=1;j<=n;j++)
{
for(i=0;i<b[m];i++) f[i][j&1]=-1;
for(i=0;i<b[m];i++)
if(f[i][(j-1)&1]!=-1)
{
v=i;
s[0]=1;
for(k=1;k<=m;k++)
{
s[k]=v%3;
v/=3;
}
dfs(j,i,1,0,0);
}
}
int ans=-1;
for(i=0;i<b[m];i++)
if(ans<f[i][n&1]) ans=f[i][n&1];
printf("%d\n",ans);
}
return 0;
}
posted @
2010-08-15 13:09 wuxu 阅读(316) |
评论 (0) |
编辑 收藏
BFS. bfs的时候应是一整行一整列的扩展,而不是只扩展周围四个点.见代码:
#include<iostream>
#include<queue>
using namespace std;
int dir[4][2]={0,-1,0,1,-1,0,1,0};
char board[80][80];
bool vis[80][80];
int w,h;
typedef struct
{
int x,y;
int num,cur;
}node;
int dir_lookup(int x,int y)
{
if(x==0&&y==-1) return 0;
if(x==0&&y==1) return 2;
if(x==1&&y==0) return 1;
if(x==-1,y==0) return 3;
}
int bfs(int begx,int begy,int endx,int endy)
{
node temp;
queue<node> ss;
vis[begy][begx]=true;
temp.x=begx;
temp.y=begy;
temp.cur=-1;
temp.num=0;
ss.push(temp);
while(!ss.empty())
{
temp=ss.front();
ss.pop();
node tp;
for(int i=0;i<4;i++)
{
tp.x=temp.x+dir[i][0];
tp.y=temp.y+dir[i][1];
tp.cur=dir_lookup(dir[i][0],dir[i][1]);
if(tp.cur!=temp.cur||temp.cur==-1)
tp.num=temp.num+1;
else tp.num=temp.num;
while(1)
{
if(tp.x>=0&&tp.x<=w+1&&tp.y>=0&&tp.y<=h+1&&!vis[tp.y][tp.x])
{
if(tp.x==endx&&tp.y==endy||board[tp.y][tp.x]==' ')
{
vis[tp.y][tp.x]=true;
if(tp.x==endx&&tp.y==endy)
return tp.num;
ss.push(tp);
tp.x=tp.x+dir[i][0];
tp.y=tp.y+dir[i][1];
}
else break;
}
else break;
}
}
}
return -1;
}
int main()
{
int test=1;
while(scanf("%d%d",&w,&h)!=EOF&&(w||h))
{
int i,j;
for(i=1;i<=h;i++)
{
getchar();
for(j=1;j<=w;j++)
scanf("%c",&board[i][j]);
}
for(i=0;i<=w+1;i++)
{
board[0][i]=' ';
board[h+1][i]=' ';
}
for(i=0;i<=h+1;i++)
{
board[i][0]=' ';
board[i][w+1]=' ';
}
printf("Board #%d:\n",test++);
int x1,y1,x2,y2;
int p=1;
while(scanf("%d%d%d%d",&x1,&y1,&x2,&y2)!=EOF&&(x1+y1+x2+y2))
{
printf("Pair %d: ",p++);
memset(vis,0,sizeof(vis));
int cnt=bfs(x1,y1,x2,y2);
if(cnt!=-1) printf("%d segments.\n",cnt);
else printf("impossible.\n");
}
printf("\n");
}
//system("pause");
return 0;
}
posted @
2010-08-13 17:23 wuxu 阅读(224) |
评论 (0) |
编辑 收藏
摘要: 模拟.详细见代码:
#include<iostream>#include<cstring>using namespace std;char a[7][10]={{'-',' ','-','-',' ','-','-','-','-','-'},{'|',' ',' ',' ','|','|',...
阅读全文
posted @
2010-08-13 10:52 wuxu 阅读(167) |
评论 (0) |
编辑 收藏
这到题我是用压缩DP做的，但是要是n再大一些就不能这么做了。每一行取或不取分别用1、0来表示。那么我们可以用二进制来表示每行的状态。状态转移方程为：f[i][j]=max{f[i-1][k]+sum(i,j),k为第i-1行的一个状态，且j&k==0}，sum(i,j)表示第i行满足状态j的数之和。对于每行的状态不能连续出现两个或多个1，因此可以把这种状态舍去。最后用滚动数组。详细见代码：
#include<iostream>
using namespace std;
int n;
int map[21][21];
int dp[2][1<<20+1];
int s[1<<20+1];
int bit[21];
int main()
{
int i,j,k;
bit[1]=1;
for(i=1;i<n;i++) bit[i+1]=1<<i;
int top=0;
for(i=0;i<(1<<20);i++)
{
for(j=1;j<20;j++)
{
if((i&(1<<(j-1)))&&(i&(1<<j)))
break;
}
if(j==20) s[top++]=i;
}
while(scanf("%d",&n)!=EOF)
{
int ans=0;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&map[i][j]);
memset(dp,0,sizeof(dp));
for(i=1;i<=n;i++)
{
for(j=0;j<top;j++)
{
int temp=0;
if(s[j]>=(1<<n)) break;
for(k=1;k<=n;k++)
{
if(s[j]&(1<<(k-1)))
temp+=map[i][k];
}
int minn=0;
for(k=0;k<top;k++)
{
if(s[k]>=(1<<n)) break;
if((s[k]&s[j])==0)
{
if(minn<dp[(i-1)&1][k])
minn=dp[(i-1)&1][k];
}
}
dp[i&1][j]=minn+temp;
if(ans<dp[i&1][j]) ans=dp[i&1][j];
}
}
printf("%d\n",ans);
}
return 0;
}
posted @
2010-08-12 21:08 wuxu 阅读(382) |
评论 (0) |
编辑 收藏
摘要: 图论+DP.题目要求：1、把所有的人分成2组，每组至少有1人；2、每组里的人两两认识。3、两个组的成员应尽量接近。 我们先构图，如果存在两个人A和B，A不认识B，或B不认识A，那么A和B一定不能分在同一组。因此，我们以人为结点重新构造一个图G。假如A和B不能分在同一组，那么就在G中增加一条无向边(A,B)。 然后求极大连通分量...
阅读全文
posted @
2010-08-11 23:23 wuxu 阅读(212) |
评论 (0) |
编辑 收藏DP(递归实现,并保存子问题的解).
#include<iostream>
using namespace std;
int height[105][105];
int dis[105][105];
int dir[4][2]={0,1,0,-1,-1,0,1,0};
int c,r;
int dp(int u,int v)
{
if(dis[u][v]) return dis[u][v];
dis[u][v]=1;
for(int i=0;i<4;i++)
{
int x=u+dir[i][0];
int y=v+dir[i][1];
if(x>=0&&x<r&&y>=0&&y<c&&height[u][v]>height[x][y])
{
if(!dis[x][y]) dp(x,y);
if(dis[u][v]<dis[x][y]+1)
dis[u][v]=dis[x][y]+1;
}
}
return dis[u][v];
}
int main()
{
while(scanf("%d%d",&r,&c)!=EOF)
{
int i,j;
for(i=0;i<r;i++)
for(j=0;j<c;j++)
scanf("%d",&height[i][j]);
memset(dis,0,sizeof(dis));
for(i=0;i<r;i++)
for(j=0;j<c;j++)
dp(i,j);
int ans=0;
for(i=0;i<r;i++)
for(j=0;j<c;j++)
if(ans<dis[i][j])
ans=dis[i][j];
printf("%d\n",ans);
}
return 0;
}
posted @
2010-08-11 17:31 wuxu 阅读(136) |
评论 (0) |
编辑 收藏
枚举+最短路
枚举最低等级,保证酋长在交易范围,然后求最短路。
#include<iostream>
using namespace std;
const int inf=100000000;
int m,n;
int map[105][105];
int dis[105],vis[105],lev[105];
int dijkstra()
{
int ans=inf;
int i,j,k;
for(i=lev[1]-m;i<=lev[1];i++)
{
memset(vis,0,sizeof(vis));
for(j=1;j<=n+1;j++)
dis[j]=map[1][j];
vis[1]=1;
for(j=1;j<=n;j++)
{
int min=inf,cur=-1;
for(k=1;k<=n+1;k++)
{
if(!vis[k]&&lev[k]>=i&&lev[k]<=i+m&&dis[k]<min)
{
min=dis[k];
cur=k;
}
}
if(cur==-1) break;
vis[cur]=1;
for(k=1;k<=n+1;k++)
{
if(!vis[k]&&lev[k]>=i&&lev[k]<=i+m&&map[cur][k]!=inf&&dis[k]>dis[cur]+map[cur][k])
dis[k]=dis[cur]+map[cur][k];
}
}
if(dis[n+1]<ans)
ans=dis[n+1];
}
return ans;
}
int main()
{
int p,l,x,t,v;
int i,j;
scanf("%d%d",&m,&n);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(i==j) map[i][j]=0;
else map[i][j]=inf;
}
for(i=1;i<=n;i++)
{
scanf("%d%d%d",&p,&l,&x);
map[i][n+1]=p;
lev[i]=l;
for(j=1;j<=x;j++)
{
scanf("%d%d",&t,&v);
map[i][t]=v;
}
}
lev[n+1]=lev[1];
printf("%d\n",dijkstra());
return 0;
}
posted @
2010-08-11 16:40 wuxu 阅读(224) |
评论 (0) |
编辑 收藏