链接：http://acm.hdu.edu.cn/showproblem.php?pid=1166

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1042
这道题是大数和普通数的乘法，步骤如下：
1、判断乘后大数的位数，此题约为40000；
2、选择由那种类型数组存储，一般由int存储，一个数能存5位（10000*100000<2^31）；
3、确定数组长度，此题约为40000/5=8000；
4、计算数组中每个数与普通数的乘积并存入数组；
5、计算数组中每个数乘普通数的进位，加入高一位数组；
6、输出时先计算使用了多少个的数组，然后向前输出数组。

题目链接：http://acm.pku.edu.cn/JudgeOnline/problem?id=1609
方法一：转化为求一维最长上升子序列。O(nlogn)

方法二：状态转移方程为：f[i][j]=max{f[i-1][j],f[i][j-1]}+a[i][j].
O(n^2)代码：
O(nlogn)代码：
题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4007
很好的一道题目，用f[i,j]表示前i个学生分为j个班时的最小unhappy值，状态转移方程为：f[i,j]=min{f[k,j-1],+(sum[i]-sum[k])*g[j]}.其中a<=i-k<=b,sum[i] = sigma {(x[s] -L)^2 | s≤ i}.
但现在的时间复杂度为O(k*n^2)，显然会TLE。将转移方程整理一下：f[i,j]=sum[i]*g[j]+min{f[k,j-1]-sum[k]*g[j]}. 显然可维护一个单调递增队列，每次转移之前将新的可选状态从队列尾插入，同时保证队列头的元素在可选范围之内。这样每次转移就可以只取队列头的元素，总的时间复杂度为O(n*k).

 

简单DP      题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3127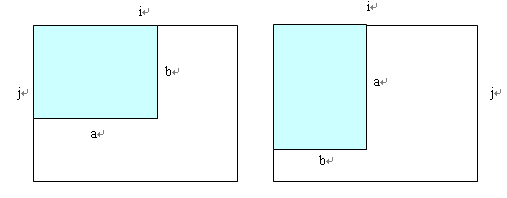

状态转移方程：f[i,j]=max{f[i,j],f[i-a,j]+f[a,j-b]+p,f[i,j-b]+f[i-a,b]+p}
                  f[i,j]=max{f[i,j],f[i-b,j]+f[b,j-a]+p,f[i,j-a]+f[i-b,a]+p}
RMQ(Range Minimum/Maximum Query)问题是求区间最值问题，用ST算法，可以做到O(nlogn)的预处理，O(1)地回答每个询问。
以求最大值为例，设f[i,j]表示以i为起点，长度为2^j这个区间中的最大值，即[i,i+2^j-1]这个区间内的最大值，那么在询问[a,b]区间的最大值时答案就是max(f[a,k], f[b-2^k+1,k]),其中k是满足2^k<=b-a的最大的k，即k=ln(b-a+1)/ln(2);另外,这两个区间必须覆盖[a,b].
f的求法可以用动态规划，f[i,j]=max(f[i,j-1],f[i+2^(j-1),j-1]).

题目链接：http://acm.pku.edu.cn/JudgeOnline/problem?id=3264

#include<iostream>
#include<cmath>
#define max(a,b) (a>b?a:b)
#define min(a,b) (a<b?a:b) 
using namespace std;
int n,q,a,b;
int h[50005];
int maxn[50005][16];
int minn[50005][16];
void st_init()
{
     for(int i=1;i<=n;i++) 
     maxn[i][0]=minn[i][0]=h[i];
     int m=int(log(double(n))/log(2.0));
     for(int i=1;i<=m;i++)
     for(int j=1;j<=n;j++)
     {
          maxn[j][i]=maxn[j][i-1];
          if(j+(1<<(i-1))<=n) 
          maxn[j][i]=max(maxn[j][i],maxn[j+(1<<(i-1))][i-1]);
     }
     
     for(int i=1;i<=m;i++)
     for(int j=1;j<=n;j++)
     {
          minn[j][i]=minn[j][i-1];
          if(j+(1<<(i-1))<=n)
          minn[j][i]=min(minn[j][i],minn[j+(1<<(i-1))][i-1]);
     }    
}
int st_search(int l,int r)
{
    int m=int(log(double(r-l+1))/log(2.0));
    int mx=max(maxn[l][m],maxn[r-(1<<m)+1][m]);
    int mn=min(minn[l][m],minn[r-(1<<m)+1][m]);
    return mx-mn;
}
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)
    scanf("%d",&h[i]);
    st_init();
    for(int i=1;i<=q;i++)
    {
        scanf("%d%d",&a,&b);
        printf("%d\n",st_search(a,b));
    }
    //system("pause");
    return 0;
}

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3401
用f[i][j]表示第i天股票数为j的最大收益，f[i][j]可以从以下三个地方得到：
1、在上次交易的基础上再买一些: f[i][j]=max{f[i][j],f[r][k]-(j-k)*b_price[i]} 0<r<i-w, 0<=j-k<=b_num[i]
2、在上次交易的基础上卖出一些: f[i][j]=max{f[i][j],f[r][k]+(k-j)*s_price[i]} 0<r<i-w, 0<=k-j<=s_num[i]
3、当天股票不动: f[i][j]=max{f[i][j],f[i-1][j]}
这样的时间复杂度为O(T^2*MaxP^2)，需要做一些优化.
对于买股票的时候，f[r][k]-(j-k)*b_price[i]=f[r][k]+k*b_price[i]-j*b_price[i] ,(j>= k>=j-b_num[i]),f[i][j]的最优值由f[r][k]+k*b_price[i]确定，由递推方程可知，f[r][k]始终是股票数为k的最大值.  对于某个j，f[r][k]+k*b_price[i]已经重复求过了，这次只需要求f[r][j]+j*b_price[i]即可,因此可以用单调队列来保存这些信息,并且可以方便的取出最大值。  卖股票的情况也同上面类似。此时的时间复杂度为O(T*MaxT).
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3560
题意：求连通分量的个数和环图的个数。如果是环图那么每个点的度数应该为2。