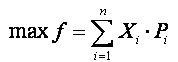
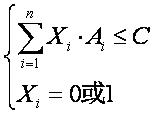
用动态规划法可以找出这个服务器上的最优存储方法，然后把已经存储过的那些信息块删去，然后对下一个服务器采用同样的背包规划。直到再增加服务器已经不能节省开销，即新服务器的价格F大于此服务器上存储的信息的总通讯费 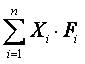   就停止计算。

四．模型求解

1．背包问题的求解：（动态规划法）

   

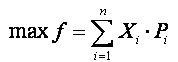
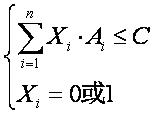
按可存储的信息块数划分为n个阶段。

状态变量S表示用于存储第一种物品至第n种物品的总存储量。

则状态转移方程为：

允许决策集合为：

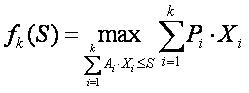
最优值函数fk(S)是当总存储量不超过S时，服务器可以装入第1个到第n个信息块的最大节省费用。

即

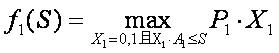
    因而可写出动态规划的顺序递推关系为：

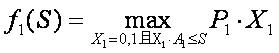
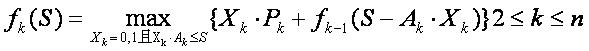
然后编程逐步计算出fk(S)及相应的决策函数Xk最后得出的fn(C)就是所求的最大值，其相应的最优策略由反推运算即可得出。

根据上述算法用C语言编程，求得第一个服务器对应的决策函数及其总共节省费用值如下：

总节省费用：2M+0.423828万元。

使用容量：487MB。

然后去掉第1，3，5，11个信息块，同法对第二个服务器做0—1背包规划，得：

编号i	2	4	6	7	8	9	10	12
Xi	1	0	0	0	0	0	0	0
编号i	13	14	15	16	17	18	19
Xi	0	0	0	1	0	0	0

总节省费用：M+0.398047万元。

使用容量：452MB。

然后去掉第2，16个信息块，以此类推，结果如下：

第三个服务器：

总节省费用：0.297266万元。

使用容量411MB。

第四个服务器：

总节省费用：0.144922万元。

使用容量361MB。

第五个服务器：

总节省费用：0.089844万元。

使用容量：338MB。

第六个服务器：

总节省费用：0.001563万元。

使用容量：460MB。

剩下的4，8，9，10，13，15，17，19个信息块的当量节省价格都为负，所以再购买服务器一定不合算。算法终止。

2．剩余内存的处理以及购买服务器的必要性分析。

可以注意到，由上述算法得到存储方法，每个服务器的容量是有剩余的。由实际经验可知，利用这些存储空间，即使是下载一些通讯费用比较低，也就是原本不适宜下载的信息，也是合算的。这样，我用贪心法来分配那些多余的空间。

目前算得的六个服务器的存储状况如下：

服务器编号	1	2	3	4	5	6
剩余存储量（MB）	25	60	101	151	174	52
存储情况（信息块编号）	1，3，5，11	2，16	7，18	6	12，14	10

未存储的信息块情况：

用贪心法对服务器存储状况表进行调整：

服务器编号	1	2	3	4	5	6
剩余存储量（MB）	25	60	24	47	17	52
存储情况	1，3，5，11	2，16	7，18，17	6，8	12，14，15	10

然后，分别对每个服务器进行计算，如果它所存储的所有信息块总共的通讯费用低于购买服务器的费用的话，这台服务器就是不必要的。计算结果如下表（内部信息的通讯费看作一个大值Y）：

服务器编号	1	2	3	4	5	6
信息通讯总费(万元)	2Y+0.6	Y+0.9	1.2	1.05	1.05	0.9

已知每个服务器的价格是1万元，所以第六个服务器不应购买。

五．模型推广：

如果有多种型号的服务器，只需将上边的算法做一些改动，仍然能够求解。例如有两种容量和价格不相同的服务器。我仍旧一台一台地挑选来决定其是否使用以及存储的情况。每次挑选的时候，对两种型号的服务器各做一次0—1背包规划，比较两种情况各自的存储信息块的通讯总费用，选择大的录用。然后删去已存储的信息块，反复上述操作。就得到各台服务器的型号以及存储状况。算法的终止条件和同一型号的情况相同。

六．参考文献：

运筹学（第三版），清华大学出版社，北京，2005.6

附录：

//背包问题的C语言程序实现

#include<stdio.h>

#define C 512  //内存容量

#define N 19   //信息块数量

#define M 10   //设内部信息块的当量节省价格为10

double f[20][520];//最优值函数

int main()

{

    int A[20],X[20],b;

    double P[20],maxn,a;

    int i,j,k;

    freopen("out.txt","w",stdout);

    freopen("in.txt","r",stdin);//数据读入

    for(j=1;j<=N;j++)

        scanf("%d",&A[j]);

    for(j=1;j<=N;j++)

        scanf("%lf",&P[j]);

    for(j=0;j<A[1];j++)//DP过程

        f[1][j]=0;

    for(;j<=C;j++)

        f[1][j]=P[1];

    for(i=2;i<=N;i++)

        for(j=0;j<=C;j++)

        {

            if(j-A[i]>=0)

                a=P[i]+f[i-1][j-A[i]];

            else a=0;

            if(a>f[i-1][j])

                f[i][j]=a;

            else f[i][j]=f[i-1][j];

        }

    for(i=N,b=C;i>0;i--)//反推过程

    {

        if(f[i][b]==f[i-1][b]) X[i]=0;

        else

        {

            X[i]=1;

            b-=A[i];

        }

    }

    for(i=1;i<=N;i++)

        printf("X%d=%d\n",i,X[i]);

    printf("f=%lf\n",f[N][C]);

    return 0;

}