置顶随笔
#
搬家到
http://www.cnblogs.com/schindlerlee/
1.想要代码的可以email我
2.分享你的知识
3.尊重他人的隐私
4.给自己网上留个好印象
5.平心静气地争论
6.尊重别人的时间和带宽
7.本人坚持原创,转载请注明出处。
2010年11月4日
#
The criminals in this town used to believe in things. Honor. Respect.
Look at you! What do you believe in? What do you believe in?
--from <<Dark Knight>>
2010年10月26日
#
马克思都说了“反对倾向性的法律,即没有规定客观标准的法律,乃是恐怖主义的法律”。只是对于宪法写的和实际的感受完全相反的时候你总是会感觉很恼火的,特别宪法第一条就写着坚持马克思主义,那么法治这个说法就显得很滑稽了。
原文:http://jackyhds.wordpress.com/2010/01/21/imdb%E8%A2%AB%E5%A2%99/
2010年7月8日
#
1 /*
2 * SOUR:zju2589
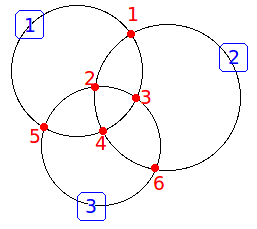
3 * ALGO:computational geomtry 计算平面上不重合的n个圆形成的区域
4 * 基本的方法,如图所示,将所有圆之间的交点作为点,将在同一个圆上的所有交点之间的弧作
5 * 为边建立一张有向图,之后可以利用平面图的欧拉定理
6 * V - E + F = 2
7 * 由于V已知,E已知,F就可以求出来了。
8 * 由于欧拉定理是对一张无向连通图成立的,如果图有多个连通块的时候需要对欧拉定理做一些
9 * 修改。由于多个有向图的面共享最外边的面,所以设联通块的个数为n
10 * V - E + F = 2 * n , 但是需要减去n个联通块共享的最大平面
11 * 所以 F = n + 1 + E - V;
12 * DATE: 2010年 07月 08日 星期四 14:49:41 CST
13 * COMM:5
14 * */
15 const int N = 64;
16 const double eps = 1e-8;
17 int n, vis[N], g[N][N];
18 double r[N];
19 struct point_t {
20 double x, y;
21 point_t(){}
22 point_t(double a, double b){x = a, y = b;}
23 }c[N];
24
25 int dcmp(double x) { return (x > eps) - (x < -eps);}
26 bool operator < (point_t a,point_t b)
27 {
28 if (dcmp(a.x - b.x)) {
29 return a.x < b.x;
30 }
31 return dcmp(a.y - b.y) < 0;
32 }
33
34 point_t operator + (point_t a, point_t b) { return point_t(a.x+b.x, a.y+b.y);}
35 point_t operator - (point_t a, point_t b) { return point_t(a.x-b.x, a.y-b.y);}
36 double dist(point_t a, point_t b) { return hypot(a.x-b.x, a.y-b.y);}
37 double sqr(double x) { return x * x;}
38 point_t normal(point_t a) { return point_t(a.x / hypot(a.x, a.y), a.y / hypot(a.x, a.y));}
39 point_t scale(point_t a, double fac) { return point_t(a.x * fac, a.y * fac);}
40 bool intersect(point_t c1, double r1, point_t c2, double r2, point_t &a, point_t &b)
41 {
42 double d = dist(c1, c2);
43 if (d < fabs(r1 - r2) - eps || d > r1 + r2 + eps) {
44 return false;
45 }
46 double len = (sqr(r1) - sqr(r2) + sqr(d)) / 2.0 / d;
47 double h = sqrt(sqr(r1) - sqr(len));
48 point_t t = normal(c2 - c1);
49 point_t p = c1 + scale(t, len);
50 point_t v = scale(point_t(-t.y, t.x), h);
51 a = p + v, b = p -v;
52 return true;
53 }
54
55 void init()
56 {
57 int i;
58 memset(g, 0, sizeof(g));
59 memset(vis, 0, sizeof(vis));
60 for (i = 0;i < n;i++) {
61 g[i][i] = 1;
62 }
63 }
64
65 int main()
66 {
67 int testcase, i, j, k;
68 scanf("%d", &testcase);
69 while (testcase--) {
70 scanf("%d", &n);
71 set <point_t> allpoint, p[64];
72 for (i = 0;i < n;i++) {
73 scanf("%lf %lf %lf", &c[i].x, &c[i].y, &r[i]);
74 }
75 init();
76 for (i = 0;i < n;i++) {
77 for (j = i + 1;j < n;j++) {
78 point_t a, b;
79 if (intersect(c[i], r[i], c[j], r[j], a, b)) {
80 allpoint.insert(a), allpoint.insert(b);
81 p[i].insert(a), p[i].insert(b);
82 p[j].insert(a), p[j].insert(b);
83 g[i][j] = g[j][i] = 1;
84 }
85 }
86 }
87 for (k = 0;k < n;k++) {
88 for (i = 0;i < n;i++) {
89 for (j = 0;j < n;j++) {
90 g[i][j] |= g[i][k] & g[k][j];
91 }
92 }
93 }
94 int f = 1;
95 for (i = 0;i < n;i++) {
96 f += p[i].size();
97 if (!vis[i]) {
98 f += 1;
99 for (j = 0;j < n;j++) {
100 vis[j] |= g[i][j];
101 }
102 }
103 }
104 f -= allpoint.size();
105 printf("%d\n", f);
106 }
107 return 0;
108 }
109
110
1 /*
2 * SOUR:pku3334
3 * ALGO:二分高度,求水平线和多边形的交点,求出多边形面积
4 * DATE: 2010年 07月 07日 星期三 22:29:14 CST
5 * */
6 const int N = 1024;
7 struct point_t {
8 double x, y;
9 point_t (){}
10 point_t (double a, double b){x = a, y = b;}
11 }P[N], Q[N];
12 int m, n, cp, cq;
13 double area;
14
15 point_t operator + (point_t a, point_t b) { return point_t(a.x + b.x, a.y + b.y);}
16 point_t operator - (point_t a, point_t b) { return point_t(a.x - b.x, a.y - b.y);}
17 double SQR(double x ){ return x * x;}
18 double dist(point_t a) { return sqrt(SQR(a.x) + SQR(a.y));}
19 double dist(point_t a, point_t b) { return dist(a-b);}
20 double cross_mul(point_t a, point_t b) { return a.x * b.y - a.y * b.x;}
21 const double eps = 1e-10;
22
23 double calcu(point_t p[], int n, int cusp, double h)
24 {
25 double ans = 0;
26 int i, j, k, beg = 0, end = n - 1;
27 if (h <= p[cusp].y) {
28 return 0;
29 }
30 for (i = 0;i < cusp;i ++) {
31 if (p[i].y >= h && h >= p[i+1].y) {
32 beg = i;break;
33 }
34 }
35 for (i = n - 2;i >= cusp;i--) {
36 if (p[i].y <= h && h <= p[i+1].y) {
37 end = i;break;
38 }
39 }
40
41 point_t a = point_t(p[beg].x + (h - p[beg].y) * (p[beg+1].x - p[beg].x)
42 / (p[beg+1].y - p[beg].y) , h);
43 point_t b = point_t(p[end].x + (h - p[end].y) * (p[end+1].x - p[end].x)
44 / (p[end+1].y - p[end].y) , h);
45 ans += cross_mul(a, p[beg+1]) + cross_mul(p[end], b) + cross_mul(b, a);
46 for (i = beg + 1;i <= end - 1;i++) {
47 ans += cross_mul(p[i], p[i+1]);
48 }
49 return fabs(ans / 2.0);
50 }
51
52 int main()
53 {
54 int testcase, i;
55 scanf("%d", &testcase);
56 while (testcase--) {
57 scanf("%lf", &area);
58 scanf("%d", &m); for (i = 0;i < m;i++) { scanf("%lf %lf", &P[i].x, &P[i].y); }
59 scanf("%d", &n); for (i = 0;i < n;i++) { scanf("%lf %lf", &Q[i].x, &Q[i].y); }
60 for (i = 1;i < m-1;i++) {
61 if (P[i-1].y >= P[i].y && P[i].y <= P[i+1].y) {
62 cp = i;
63 }
64 }
65 for (i = 1;i < n-1;i++) {
66 if (Q[i-1].y >= Q[i].y && Q[i].y <= Q[i+1].y) {
67 cq = i;
68 }
69 }
70 double L = min(P[cp].y , Q[cq].y),
71 R = min(min(P[0].y, P[m - 1].y) , min(Q[0].y, Q[n - 1].y)) ;
72 while (L + eps < R) {
73 double mid = (L + R) / 2.0;
74 double A = calcu(P, m, cp, mid) + calcu(Q, n, cq, mid);
75 //printf("h = %.3f, A = %.3f\n", mid, A);
76 if (A <= area) {
77 L = mid;
78 }else {
79 R = mid;
80 }
81 }
82 printf("%.3f\n", L);
83 }
84 return 0;
85 }
86
87
88
2010年7月7日
#
二分半径,将求解问题变成判断性问题。
利用求圆交面积的方法判断可行性。


1
2 const int N = 32;
3 const double eps = 1e-7;
4
5 struct circle_t {
6 double r, x, y;
7 circle_t (){}
8 circle_t (double a, double b, double c){r = a, x = b, y = c;}
9 }c[N];
10 int n;
11 double ans;
12 double area[N];
13
14 const double pi = acos(-1.0);
15 double SQR(double x) { return x * x;}
16
17 double intersect(circle_t c1, circle_t c2)
18 {
19 double ans = 0;
20 double d = sqrt(SQR(c1.x - c2.x) + SQR(c1.y - c2.y));
21 if (c1.r < c2.r) {
22 swap(c1, c2);
23 }
24 if (d >= c1.r + c2.r) { return 0; }
25 if (d <= c1.r - c2.r) { return pi * SQR(c2.r); }
26 double angle1 = acos((SQR(c1.r) + SQR(d) - SQR(c2.r)) / 2.0 / c1.r / d); //half
27 double angle2 = acos((SQR(c2.r) + SQR(d) - SQR(c1.r)) / 2.0 / c2.r / d);
28 ans -= d * c1.r * sin(angle1);
29 ans += angle1 * SQR(c1.r) + angle2 * SQR(c2.r);
30 return ans;
31 }
32
33 bool judge(circle_t umbrella)
34 {
35 int i,j,k;
36 for (i = 0;i < n;i++) {
37 if (intersect(umbrella, c[i]) < area[i]/2) {
38 return false;
39 }
40 }
41 return true;
42 }
43
44 double calcu(int idx)
45 {
46 int i,j,k;
47 double L = 0, R = 200000.0;
48 while (L + eps < R) {
49 double mid = (L + R) / 2.0;
50 if (judge(circle_t(mid, c[idx].x, c[idx].y))) {
51 R = mid;
52 }else {
53 L = mid;
54 }
55 }
56 return L;
57 }
58
59 int main()
60 {
61 int testcase, i;
62 scanf("%d", &testcase);
63 while (testcase--) {
64 scanf("%d", &n);
65 for (i = 0;i < n;i++) {
66 scanf("%lf %lf %lf", &c[i].x, &c[i].y, &c[i].r);
67 area[i] = pi * SQR(c[i].r);
68 }
69 ans = 200000.0;
70 for (i = 0;i < n;i++) {
71 ckmin(ans, calcu(i));
72 }
73 printf("%.4f\n", ans);
74 }
75 return 0;
76 }
77
78
79
练练手可以,不会就看算法导论吧。。
1 const int N = 100010;
2
3 struct point_t {
4 double x, y;
5 }p[N], Y[N];
6
7 double sqr(double x) { return x * x;}
8 bool cmp1(const point_t &a, const point_t &b)
9 {
10 if (a.x != b.x) {
11 return a.x < b.x;
12 }
13 return a.y < b.y;
14 }
15
16 bool cmp2(const point_t &a,const point_t &b)
17 {
18 if (a.y != b.y) {
19 return a.y < b.y;
20 }
21 return a.x < b.x;
22 }
23
24 const double inf = 1e100;
25 double dist(point_t a,point_t b) { return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));}
26 int top;
27
28 double divide(int beg, int end)
29 {
30 double ans = inf;
31 int i,j;
32 if (end < beg + 3) {
33 for (i = beg;i <= end;i++) {
34 for (j = i + 1;j <= end;j++) {
35 ckmin(ans, dist(p[i], p[j]));
36 }
37 }
38 return ans;
39 }
40 int mid = (beg + end) >> 1, cnt;
41 ckmin(ans, divide(beg, mid));
42 ckmin(ans, divide(mid + 1, end));
43 for (i = beg, top = 0;i <= end;i++) {
44 if (fabs(p[i].x - p[mid].x) < ans) {
45 Y[top++] = p[i];
46 }
47 }
48 sort(Y, Y + top, cmp2);
49 for (i = 0;i < top;i++) {
50 for (cnt = 0,j = i + 1;j < top && cnt < 7;cnt++, j++) {
51 ckmin(ans, dist(Y[i], Y[j]));
52 }
53 }
54 return ans;
55 }
56
57 int n;
58 void proc()
59 {
60 int i,j,k;
61 sort(p, p + n, cmp1);
62 double ans = divide(0, n - 1);
63 printf("%.2f\n", ans/2.0);
64 }
65
66 int main()
67 {
68 int i,j,k;
69 while (scanf("%d", &n) == 1 && n) {
70 for (i = 0;i < n;i++) {
71 scanf("%lf %lf", &p[i].x, &p[i].y);
72 }
73 proc();
74 }
75 return 0;
76 }
77
要注意判断圆的左边不能找过y轴。
算法不解释。


1
2 const int N = 1024;
3 const double eps = 1e-10;
4 struct circle_t {
5 double r, x, y;
6 circle_t() {}
7 circle_t(double a, double b, double c) {r = a, x = a, y = b;}
8 }c[N];
9 int pt[N], n;
10
11 double sqr(double x ) { return x * x;}
12 double proj(circle_t &a, circle_t &b)
13 { return sqrt(sqr(a.r + b.r) - sqr(a.r - b.r)); }
14
15 double intersect(circle_t &a, circle_t &b)
16 {
17 double l = sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
18 double r = a.r + b.r;
19 return l - r < -eps;
20 }
21
22
23 double calcu()
24 {
25 int i,j,k;
26 double width = c[1].r;
27 c[1].x = c[1].y = c[1].r;
28 for (i = 2;i <= n;i++) {
29 double x = 1e100;
30 for (j = i - 1;j >= 1;j--) {
31 c[i].x = max(c[i].r, c[j].x + proj(c[i], c[j]));
32 if (c[i].x <= c[i-1].x) { continue; }
33 for (k = 1;k < i;k++) {
34 if (k == j) { continue; }
35 if (intersect(c[k], c[i])) {
36 break;
37 }
38 }
39 if (k == i) { // success
40 ckmin(x, c[i].x);
41 pt[j] = i;
42 }
43 }
44 c[i].x = x;
45 ckmax(width, c[i].x + c[i].r);
46 }
47 return width;
48 }
49
50 int ans[N], top;
51 int main()
52 {
53 int i,j;
54 scanf("%d", &n);
55 for (i = 1;i <= n;i++) {
56 scanf("%lf", &c[i].r);
57 c[i].x = c[i].r;
58 c[i].y = c[i].r;
59 pt[i] = i;
60 }
61 double width = calcu();
62 int beg = 1, end = n;
63 for (i = 1;i <= n;i++) {
64 //printf("pt[%d] = %d\n", i, pt[i]);
65 if (c[i].r == c[i].x) {
66 beg = i;
67 }
68 }
69 for (i = 1;i < beg;i++) {
70 ans[top++] = i;
71 }
72 for (i = n;i >= 1;i--) {
73 if (c[i].x + c[i].r == width) {
74 end = i;
75 }
76 }
77 //printf("beg = %d, end = %d\n", beg, end);
78 for (i = beg;i < end;i = pt[i]) {
79 for (j = i + 1;j < pt[i];j++) {
80 ans[top++] = j;
81 }
82 }
83 for (i = end + 1;i <= n;i++) {
84 ans[top++] = i;
85 }
86 printf("%d\n", top);
87 for (i = 0;i < top;i++) {
88 printf("%d\n", ans[i]);
89 }
90
91 return 0;
92 }
93
94
用二进制表示是否已经被吃掉,最后输出所有只剩下一个的状态。
要注意的是状态转移时候的概率要除以所有可能转移数才是正确的概率


1
2 const int N = 19;
3 #define bin(x) (1 << (x))
4 #define L(x) ((x) << 1)
5 #define R(x) ((x) >> 1)
6 #define low(x) ((x) & (-x))
7 double g[N][N];
8 double prob[bin(N)];
9 int n, full;
10 int main()
11 {
12 int i,j,s;
13 scanf("%d", &n);
14 for (i = 0;i < n;i++) {
15 for (j = 0;j < n;j++) {
16 scanf("%lf", &g[i][j]);
17 }
18 }
19 full = bin(n) - 1;
20 prob[full] = 1.0;
21 for (s = full;s > 0;s--) {
22 double bit = countbit(s);
23 bit = bit * (bit - 1) / 2;
24 for (i = 0;i < n;i++) { if (!(s & bin(i))) { continue; }
25 for (j = i + 1;j < n;j++) { if (!(s & bin(j))) { continue; }
26 prob[s - bin(j)] += prob[s] * g[i][j] / bit;
27 prob[s - bin(i)] += prob[s] * g[j][i] / bit;
28 }
29 }
30 }
31 for (i = 0;i < n;i++) {
32 printf("%.6f ", prob[bin(i)]);
33 }
34 putchar(10);
35 return 0;
36 }
37
2010年6月21日
#
摘要: 昨天学习了一下AC自动机是什么东西,做了三道题至于AC自动机的详细解释和资料可以通过搜索 Aho Corasick 找到很多相关论文和资料,我就不要班门弄斧了。第一道hdu 2222,AC自动机的基本是用方法,直接应用在多模式匹配上。第二道pku 2778 利用AC自动机减少状态量,之后将状态转移做成矩阵,利用矩阵的二分乘法得到log级别的复杂度。第三道pku 3691 使用同样是利用AC自动机减...
阅读全文
2010年6月16日
#
三维凸包的求解如果有四点共面,那么就比较繁琐了。
增量法,每次添加一个点,然后更新凸包。
关于增量法的图示看这里:
http://www.cse.unsw.edu.au/~lambert/java/3d/hull.html
现在的主要问题就是,一直所有面的法向量,如何更新凸包。
法向量点乘一个向量,可以得到这个向量在法向量上的偏移,如果这个偏移是正的,说明这个向量相关的点在面的上方,负的是下方,所以只要找到一条边关联的两个面的点积是一正一负即可。
注意这里的所有面都是由三个点组成,且是有序的,每个边只被记录两次,一次顺时针,一次逆时针。
这里不能使用int,数值太大会越界。
1
2 const int N = 1024;
3 struct F {
4 int v[4];
5 F(){}
6 F(int a,int b,int c){ v[0] = a, v[1] = b, v[2] = c, v[3] = v[0];}
7 };
8
9 struct point_t {
10 double x, y, z;
11 point_t (){}
12 point_t (double a, double b, double c){x = a, y = b, z = c;}
13 };
14 point_t operator +(point_t a, point_t b) { return point_t (a.x + b.x, a.y + b.y, a.z + b.z);}
15 point_t operator -(point_t a, point_t b) { return point_t (a.x - b.x, a.y - b.y, a.z - b.z);}
16
17 double dot_mul(point_t a, point_t b) { return a.x * b.x + a.y * b.y + a.z * b.z;}
18 point_t cross_mul(point_t a,point_t b)
19 {
20 return point_t (a.y*b.z - b.y*a.z ,
21 a.z*b.x - b.z*a.x ,
22 a.x*b.y - b.x*a.y);
23 }
24
25 double area(point_t a, point_t b)
26 {
27 point_t v = cross_mul(a, b);
28 return sqrt(0.0 + v.x * v.x + v.y * v.y + v.z * v.z) / 2;
29 }
30
31 point_t p[N];
32 int vis[N][N], n;
33
34 int main()
35 {
36 int i, j, k;
37 scanf("%d", &n);
38 for (i = 0;i < n;i++) {
39 scanf("%lf %lf %lf", &p[i].x, &p[i].y, &p[i].z);
40 }
41 vector<F> cur;
42 cur.pb(F(0, 1, 2)), cur.pb(F(2, 1, 0));
43 for (i = 3;i < n;i++) {
44 vector<F> next;
45 for (j = 0;j < cur.size();j++) {
46 F f = cur[j];
47 point_t v = cross_mul(p[f.v[1]] - p[f.v[0]],
48 p[f.v[2]] - p[f.v[1]]);
49 int val = dot_mul(v, p[i] - p[f.v[1]]) < 0 ? -1 : 1;
50 if (val < 0) {
51 next.pb(f);
52 }
53 for (k = 0;k < 3;k++) {
54 if (vis[f.v[k+1]][f.v[k]] == 0) {
55 vis[f.v[k]][f.v[k+1]] = val;
56 }else { //http://www.cppblog.com/schindlerlee
57 if (vis[f.v[k+1]][f.v[k]] != val) {
58 if (val > 0) {
59 next.pb(F(f.v[k], f.v[k+1], i));
60 }else {
61 next.pb(F(f.v[k+1], f.v[k], i));
62 }
63 }
64 vis[f.v[k+1]][f.v[k]] = 0;
65 }
66 }
67 }
68 cur = next;
69 }
70 double ans = 0;
71 for (i = 0;i < cur.size();i++) {
72 F f = cur[i];
73 ans += area(p[f.v[0]] - p[f.v[1]], p[f.v[2]] - p[f.v[1]]);
74 }
75 printf("%.3f\n", ans);
76 return 0;
77 }
2010年6月11日
#
详见国家集训队2009论文集 14.刘聪 <<浅谈数位类统计问题>>
这到题需要非常注意复数的操作,其实完全可以讲负数转化为整数操作
也就是int转换成unsigned int
还有就是要注意,int型正数,右移补0,负数右移是补1的,
1
2 /*
3 * SOUR:spoj1182
4 * ALGO:dp, number theory, binary search
5 * DATE: 2010年 06月 08日 星期二 19:47:51 CST
6 * COMM:5
7 * */
8 #include<iostream>
9 #include<cstdio>
10 #include<cstdlib>
11 #include<cstring>
12 #include<algorithm>
13 #include<queue>
14 #include<vector>
15 #include<map>
16 using namespace std;
17 #define pb(x) push_back(x)
18 //#define X first
19 //#define Y second
20 typedef vector < int >vi;
21 typedef pair < int, int >pii;
22 typedef long long LL;
23 typedef unsigned long long ULL;
24 typedef unsigned int uint;
25
26 template <class T> void ckmin(T &a,T b) { if (a > b) { a = b; } }
27 template <class T> void ckmax(T &a,T b) { if (a < b) { a = b; } }
28 int countbit(int n) { return n == 0 ? 0 : 1 + countbit(n & (n - 1)); }
29
30 const int maxint = 0x7fffffff;
31 const long long max64 = 0x7fffffffffffffffll;
32 int cnt[40][40], sum[40];
33 int X, Y, K;
34
35 void pre()
36 //算出cnt[长度][含多少个1]的方案数
37 {
38 int i,j;
39 cnt[0][0] = 1;
40 for (i = 1;i <= 32;i++) {
41 cnt[i][0] = cnt[i-1][0];
42 for (j = 1;j <= 32;j++) {
43 cnt[i][j] = cnt[i-1][j] + cnt[i-1][j-1];
44 }
45 }
46 }
47
48 int num[40], top;
49 int summ(uint X, int R, bool flag = false)
50 {
51 memset(num, 0, sizeof(num));
52 top = 1;
53 while (X) {
54 num[top++] = X & 1;
55 X >>= 1;
56 }
57 if (flag) {
58 for (int i = 1;i <= top;i++) {
59 if (num[i] == 0) {
60 num[i] = 1;
61 for (int j = i - 1;j >= 1;j--) {
62 num[j] = 0;
63 }
64 if (i == top) { top++; }
65 break;
66 }
67 }
68 }
69 int ans = 0, one = 0, i;
70 for (i = top - 1;i >= 1;i--) {
71 if (R >= one && num[i] == 1) {
72 ans += cnt[i - 1][R - one];
73 one++;
74 }
75 }
76 return ans;
77 }
78
79 int summarize(uint X, uint Y, int digit)
80 //[X, Y] 中1的个数为digit的 数字个数
81 { return summ(Y, digit, 1) - summ(X, digit, 0); }
82
83 void proc()
84 {
85 int i, j, one = -1;
86 memset(sum, 0, sizeof(sum));
87 for (i = 0;i < 32;i++) {
88 sum[i] = summarize(X, Y, i) ;
89 if (K > sum[i]) {
90 K -= sum[i];
91 }else {
92 one = i;
93 break;
94 }
95 }
96 if (Y < X) { swap(X, Y); }
97 int left = X, right = Y;
98 while (left < right) { //binary search the value expected
99 int mid = (left + right + 1) / 2;
100 if (summarize(X, mid, one) <= K) {
101 left = mid;
102 }else {
103 right = mid - 1;
104 }
105 }
106 while (countbit(left) != one) { left --; } // attention
107
108 int ans = 0;
109 for (i = 0;i < 32;i++) {
110 if (left & (1 << i)) {
111 ans |= 1 << i;
112 }
113 }
114 printf("%d\n", ans);
115 }
116
117 int main()
118 {
119 int i, j, testcase;
120 pre();
121 scanf("%d", &testcase);
122 while (testcase-- ) {
123 scanf("%d %d %d", &X, &Y, &K);
124 proc();
125 }
126 return 0;
127 }
128
2010年6月8日
#
2010-06-08 23:24:36.ural1057 number theory and dp 数位类统计问题
不说了,详见国家集训队2009论文集 14.刘聪 <<浅谈数位类统计问题>>
需要非常注意边界条件的处理.
1 /*
2 * SOUR:ural 1057
3 * ALGO:number theory and binary tree, in other word enumerate the highest digit,
4 * and use dp to reduce calculation.
5 * DATE: 2010年 06月 08日 星期二 16:44:45 CST
6 * COMM:
7 * */
8
9 using namespace std;
10 #define pb(x) push_back(x)
11 #define X first
12 #define Y second
13 typedef vector < int >vi;
14 typedef pair < int, int >pii;
15 typedef long long LL;
16 template <class T> void ckmin(T &a,T b) { if (a > b) { a = b; } }
17 template <class T> void ckmax(T &a,T b) { if (a < b) { a = b; } }
18 int countbit(int n) { return n == 0 ? 0 : 1 + countbit(n & (n - 1)); }
19
20 const int maxint = 0x7fffffff;
21 const long long max64 = 0x7fffffffffffffffll;
22 int X, Y, K, B;
23 int cnt[40][40];
24
25 void pre ()
26 {
27 int i, j;
28 cnt[0][0] = 1;
29 for (i = 1;i <= 32;i++) {
30 cnt[i][0] = cnt[i-1][0];
31 for (j = 1;j <= 32;j++) {
32 cnt[i][j] = cnt[i-1][j] + cnt[i-1][j-1];
33 }
34 }
35 }
36
37 void changeBase(int X, int num[], int &top)
38 {
39 top = 1;
40 while (X > 0) {
41 num[top++] = X % B;
42 X /= B;
43 }
44 }
45
46 void plus_one(int num[], int &top)
47 {
48 int i,j;
49 for (i = 1;i <= top;i++) {
50 if (num[i] == 0) {
51 num[i] = 1;
52 for (j = i - 1;j >= 1;j--) {
53 num[j] = 0;
54 }
55 break;
56 }
57 }
58 if (i == top) {
59 top++;
60 }
61 }
62
63 bool floor(int num[], int top)
64 {
65 int i,j;
66 for (i = top - 1;i >= 1;i--) {
67 if (num[i] > 1) {
68 for (j = i;j >= 1;j--) {
69 num[j] = 1;
70 }
71 break;
72 }
73 }
74 if (i >= 1) {
75 return true;
76 }
77 return false;
78 }
79
80 int num[40], top;
81 int proc(int X,bool flag = false)
82 {
83 memset(num, 0, sizeof(num));
84 changeBase(X, num, top);
85 if (floor(num, top) || flag) {
86 plus_one(num, top);
87 }
88
89 int ans = 0, sum = 0, i;
90 for (i = top - 1;i >= 1;i--) {
91 if (K >= sum && num[i] == 1) {
92 ans += cnt[i-1][K - sum];
93 sum++;
94 }
95 }
96 return ans;
97 }
98
99 int main()
100 {
101 pre();
102 int num[40], top, ans;
103 cin >> X >> Y >> K >> B;
104 ans = proc(Y, 1) - proc(X);
105 cout << ans << endl;
106 return 0;
107 }
2010年3月29日
#
2010年03月29日星期一.pku2166 构造
题意:要求一个序列,使这个序列进行heapsort 进行交换的次数最大。
我看到题目中有两个样例输出
n = 5: 5 4 3 2 1
n = 6: 6 5 3 2 4 1
我发现如果把6去掉,换上1,再翻下去就是5。
于是我想好像可以递推,然后就过了。。
POJ bug真多,下面的代码第一次交TLE,第二次375MS
1
2 const int N = 50100;
3 int a[N],n,len;
4 int main()
5 {
6 int i,j,k;
7 scanf("%d",&n);
8 a[1] = 1,len = 1;
9 for (k = 2;k <= n;k++) {
10 i = len;
11 while (i > 1) {
12 a[i] = a[i/2];
13 i /= 2;
14 }
15 a[1] = k;
16 a[++len] = 1;
17 }
18 for (i = 1;i <= len;i++) {
19 printf("%d ",a[i]);
20 }
21 putchar(10);
22 return 0;
23 }
24
2010年3月28日
#
2010年03月28日星期日.codeforces beta6
A:三角形两边之和大于第三边
B:暴力搜一下
C:模拟
1
2 scanf("%d\n",&n);
3 for (i = 0;i < n;i++) {
4 scanf("%d",a + i);
5 }
6 int L = 0,R = n - 1,time1 = 0,time2 = 0,ans1 = 0,ans2 = 0;
7 while (L <= R) {
8 if (time1 < time2) {
9 time1 += a[L++] ,ans1 ++;
10 }else if (time1 > time2) {
11 time2 += a[R--] ,ans2 ++;
12 }else {
13 time1 += a[L++] ,ans1 ++;
14 }
15 }
16 printf("%d %d\n",ans1,ans2);
D:题目改了,和比赛的时候不一样了,数据范围很小,dfs
E:RMQ + binary_search
给出n个数和一个范围K。
找出最长的连续的数,其中最大值和最小值的差不超过K
一个直觉的想法是
for(i = 0;i < n;i++) {
int L = a[i],R = a[i];
for (j = i + 1;j < n && R - L <= K;j++) {
更新L,R
}
更新answer
}
但是n是10^5,n^2会超时。
求区间最大值最小值可以用rmq,O(nlogn)预处理,O(1)的得到。
一定存在一个j,使得a [i ... j]合法,a[j + 1 ..n]不合法。
好的方法是二分搜索到这个j,水点的方法可以从后往前找j。
RMQ 可以线段树,也可以SparseTable
总复杂度O(nlogn)
codeforces 可以看代码,想看的会去找吧。这里的二分搜有trick,求的是upper_bound不是一般写的lower_bound,需要调整。
2010年3月20日
#
2010年03月20日星期六.sgu256.cc dp
我看到这题的第一印象就是,这可能是个水题。但是我错了。
这个题一看就是个dp,于是我就写了个5层循环的dp,死活不知道怎么错了。
后来看到了scau的代码,发现递推式基本相同,不同的是他写的是记忆化搜索.
然后我也就写了个记忆话搜索,也过了。。
1
2 #include<iostream>
3 #include<cstdio>
4 #include<cstdlib>
5 #include<cstring>
6 #include<algorithm>
7 using namespace std;
8 typedef long long LL;
9 const int maxint = 0x7fffffff;
10 const long long max64 = 0x7fffffffffffffffll;
11 const int Debug = 1;
12 const int M = 228;
13 const int N = 13;
14 const int inf = 1000000;
15
16 int dp[M][N][N][N][N], m, n, a[N], b[N];
17 void ckmin(int &a, int b) { if (a > b) { a = b; } }
18 int dfs(int balloon,int p0,int p1,int p2,int p3)
19 {
20 if (dp[balloon][p0][p1][p2][p3] < inf) {
21 return dp[balloon][p0][p1][p2][p3];
22 }
23 if (balloon >= m) {
24 return 0;
25 }
26 for (int i = 1;i <= n;i++) {
27 if (b[i] == 1 && (p0 == i)) { continue; }
28 if (b[i] == 2 && (p0 == i || p1 == i)) { continue; }
29 if (b[i] == 3 && (p0 == i || p1 == i || p2 == i)) { continue; }
30 if (b[i] == 4 && (p0 == i || p1 == i || p2 == i || p3 == i)) { continue; }
31 ckmin(dp [balloon][p0][p1][p2][p3] , dfs(balloon + a[i],i,p0,p1,p2) + 1);
32 }
33 if (dp [balloon][p0][p1][p2][p3] >= inf) {
34 dp [balloon][p0][p1][p2][p3] = dfs(balloon,0,p0,p1,p2) + 1;
35 }
36 return dp [balloon][p0][p1][p2][p3];
37 }
38//http://www.cppblog.com/schindlerlee
39 int main()
40 {
41 int i, j, k, p[4], tmp;
42 memset(dp,127,sizeof(dp));
43 //printf("%d\n",dp[0][0][0][0][0]);
44 scanf("%d %d", &m, &n);
45 for (i = 1; i <= n; i++) {
46 scanf("%d %d", a + i, b + i);
47 }
48
49 printf("%d\n", dfs(0,0,0,0,0));
50 return 0;
51 }
52