mysileng

  程序员编程艺术第十一章：最长公共子序列(LCS)问题

0、前言

    程序员编程艺术系列重新开始创作了（前十章，请参考程序员编程艺术第一~十章集锦与总结）。回顾之前的前十章，有些代码是值得商榷的，因当时的代码只顾阐述算法的原理或思想，所以，很多的与代码规范相关的问题都未能做到完美。日后，会着力修缮之。

    搜遍网上，讲解这个LCS问题的文章不计其数，但大多给读者一种并不友好的感觉，稍感晦涩，且代码也不够清晰。本文力图避免此些情况。力保通俗，阐述详尽。同时，经典算法研究系列的第三章（三、dynamic programming）也论述了此LCS问题。有任何问题，欢迎不吝赐教。

第一节、问题描述

    什么是最长公共子序列呢?好比一个数列 S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

    举个例子，如：有两条随机序列，如 1 3 4 5 5 ，and 2 4 5 5 7 6，则它们的最长公共子序列便是：4 5 5。

    注意最长公共子串（Longest CommonSubstring）和最长公共子序列（LongestCommon Subsequence, LCS）的区别：子串（Substring）是串的一个连续的部分，子序列（Subsequence）则是从不改变序列的顺序，而从序列中去掉任意的元素而获得的新序列；更简略地说，前者（子串）的字符的位置必须连续，后者（子序列LCS）则不必。比如字符串acdfg同akdfc的最长公共子串为df，而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。下文具体描述。

第二节、LCS问题的解决思路

• 穷举法   

    解最长公共子序列问题时最容易想到的算法是穷举搜索法，即对X的每一个子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列，并且在检查过程中选出最长的公共子序列。X和Y的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列，因此，X共有2^m个不同子序列（Y亦如此，如为2^n），从而穷举搜索法需要指数时间（2^m * 2^n）。

• 动态规划算法

    事实上，最长公共子序列问题也有最优子结构性质。

记:

Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

• 若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

• 若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

    由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

    行文至此，其实对这个LCS的动态规划解法已叙述殆尽，不过，为了成书的某种必要性，下面，我试着再多加详细阐述这个问题。

第三节、动态规划算法解LCS问题

3.1、最长公共子序列的结构

    最长公共子序列的结构有如下表示：

    设序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的一个最长公共子序列Z=<z₁, z₂, …, z_k>，则：

1. 若x_m=y_n，则z_k=x_m=y_n且Z_k-1是X_m-1和Y_n-1的最长公共子序列；
2. 若x_m≠y_n且z_k≠x_{m ，}则Z是X_m-1和Y的最长公共子序列；
3. 若x_m≠y_n且z_k≠y_n ，则Z是X和Y_n-1的最长公共子序列。

    其中X_m-1=<x₁, x₂, …, x_m-1>，Y_n-1=<y₁, y₂, …, y_n-1>，Z_k-1=<z₁, z₂, …, z_k-1>。

3、2.子问题的递归结构

    由最长公共子序列问题的最优子结构性质可知，要找出X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的最长公共子序列，可按以下方式递归地进行：当x_m=y_n时，找出X_m-1和Y_n-1的最长公共子序列，然后在其尾部加上x_m(=y_n)即可得X和Y的一个最长公共子序列。当x_m≠y_n时，必须解两个子问题，即找出X_m-1和Y的一个最长公共子序列及X和Y_n-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。

    由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时，可能要计算出X和Y_n-1及X_m-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算X_m-1和Y_n-1的最长公共子序列。

    与矩阵连乘积最优计算次序问题类似，我们来建立子问题的最优值的递归关系。用c[i,j]记录序列X_i和Y_j的最长公共子序列的长度。其中X_i=<x₁, x₂, …, x_i>，Y_j=<y₁, y₂, …, y_j>。当i=0或j=0时，空序列是X_i和Y_j的最长公共子序列，故c[i,j]=0。其他情况下，由定理可建立递归关系如下：

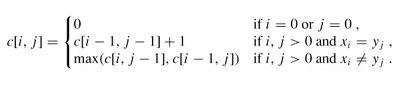
3、3.计算最优值

    直接利用上节节末的递归式，我们将很容易就能写出一个计算c[i,j]的递归算法，但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中，总共只有θ(m*n)个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

    计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储X_i与Y_j的最长公共子序列的长度，b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的，这在构造最长公共子序列时要用到。最后，X和Y的最长公共子序列的长度记录于c[m,n]中。

    由算法LCS_LENGTH计算得到的数组b可用于快速构造序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的最长公共子序列。首先从b[m,n]开始，沿着其中的箭头所指的方向在数组b中搜索。

• 当b[i,j]中遇到"↖"时（意味着xi=yi是LCS的一个元素），表示X_i与Y_j的最长公共子序列是由X_i-1与Y_j-1的最长公共子序列在尾部加上x_i得到的子序列；
• 当b[i,j]中遇到"↑"时，表示X_i与Y_j的最长公共子序列和X_i-1与Y_j的最长公共子序列相同；
• 当b[i,j]中遇到"←"时，表示X_i与Y_j的最长公共子序列和X_i与Y_j-1的最长公共子序列相同。

    这种方法是按照反序来找LCS的每一个元素的。由于每个数组单元的计算耗费Ο(1)时间，算法LCS_LENGTH耗时Ο(mn)。

3、4.构造最长公共子序列

    下面的算法LCS(b,X,i,j)实现根据b的内容打印出X_i与Y_j的最长公共子序列。通过算法的调用LCS(b,X,length[X],length[Y])，便可打印出序列X和Y的最长公共子序列。

在算法LCS中，每一次的递归调用使i或j减1，因此算法的计算时间为O(m+n)。

例如，设所给的两个序列为X=<A，B，C，B，D，A，B>和Y=<B，D，C，A，B，A>。由算法LCS_LENGTH和LCS计算出的结果如下图所示：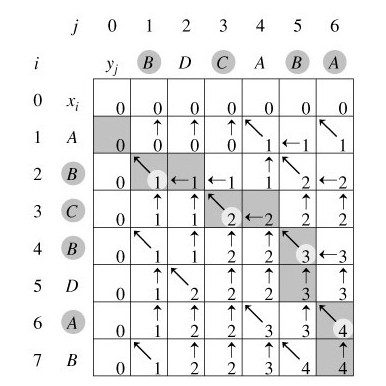

 我来说明下此图（参考算法导论）。在序列X={A，B，C，B，D，A，B}和 Y={B，D，C，A，B，A}上，由LCS_LENGTH计算出的表c和b。第i行和第j列中的方块包含了c[i，j]的值以及指向b[i，j]的箭头。在c[7,6]的项4，表的右下角为X和Y的一个LCS<B，C，B，A>的长度。对于i，j>0，项c[i，j]仅依赖于是否有xi=yi，及项c[i-1，j]和c[i，j-1]的值，这几个项都在c[i，j]之前计算。为了重构一个LCS的元素，从右下角开始跟踪b[i，j]的箭头即可，这条路径标示为阴影，这条路径上的每一个“↖”对应于一个使xi=yi为一个LCS的成员的项（高亮标示）。

    所以根据上述图所示的结果，程序将最终输出：“B C B A”。

3、5.算法的改进

    对于一个具体问题，按照一般的算法设计策略设计出的算法，往往在算法的时间和空间需求上还可以改进。这种改进，通常是利用具体问题的一些特殊性。

    例如，在算法LCS_LENGTH和LCS中，可进一步将数组b省去。事实上，数组元素c[i,j]的值仅由c[i-1,j-1]，c[i-1,j]和c[i,j-1]三个值之一确定，而数组元素b[i,j]也只是用来指示c[i,j]究竟由哪个值确定。因此，在算法LCS中，我们可以不借助于数组b而借助于数组c本身临时判断c[i,j]的值是由c[i-1,j-1]，c[i-1,j]和c[i,j-1]中哪一个数值元素所确定，代价是Ο(1)时间。既然b对于算法LCS不是必要的，那么算法LCS_LENGTH便不必保存它。这一来，可节省θ(mn)的空间，而LCS_LENGTH和LCS所需要的时间分别仍然是Ο(mn)和Ο(m+n)。不过，由于数组c仍需要Ο(mn)的空间，因此这里所作的改进，只是在空间复杂性的常数因子上的改进。

    另外，如果只需要计算最长公共子序列的长度，则算法的空间需求还可大大减少。事实上，在计算c[i,j]时，只用到数组c的第i行和第i-1行。因此，只要用2行的数组空间就可以计算出最长公共子序列的长度。更进一步的分析还可将空间需求减至min(m, n)。

第四节、编码实现LCS问题

    动态规划的一个计算最长公共子序列的方法如下，以两个序列 X、Y 为例子：

设有二维数组 f[i][j] 表示 X 的 i 位和 Y 的 j 位之前的最长公共子序列的长度，则有：

f[1][1] = same(1,1)

f[i][j] = max{f[i − 1][j − 1] +same(i,j), f[i − 1][j] ,f[i][j − 1]}

其中，same(a,b)当 X 的第 a 位与 Y 的第 b 位完全相同时为“1”，否则为“0”。

此时，f[i][j]中最大的数便是 X 和 Y 的最长公共子序列的长度，依据该数组回溯，便可找出最长公共子序列。

该算法的空间、时间复杂度均为O(n²)，经过优化后，空间复杂度可为O(n)，时间复杂度为O(nlogn)。

以下是此算法的java代码：

第五节、改进的算法

    下面咱们来了解一种不同于动态规划法的一种新的求解最长公共子序列问题的方法,该算法主要是把求解公共字符串问题转化为求解矩阵L(p,m)的问题，在利用定理求解矩阵的元素过程中（1）while(i<k),L(k,i)=null，
                  （2）while(L(k,i)=k),L(k,i+1)=L(k,i+2)=…L(k,m)=k；

    求出每列元素，一直到发现第p+1 行都为null 时退出循环，得出矩阵L(k,m)后，B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即为A 和B 的LCS，其中p 为LCS 的长度。

6.1 主要定义及定理

• 定义 1 子序列(Subsequence)：给定字符串A=A[1]A[2]…A[m]，(A[i]是A 的第i 个字母，A[i]∈字符集Σ，l<= i<m = A ， A 表示字符串A 的长度)，字符串B 是A 的子序列是指B=A[ 1 i ]A[ 2 i ]…A[ k i ],其中1 i < 2 i <…< k i 且k<=m.
• 定义2 公共子序列(Common Subsequence)：给定字符串A、B、C，C 称为A 和B 的公共子序列是指C 既是A 的子序列，又是B 的子序列。
• 定义3 最长公共子序列(Longest Common Subsequence 简称LCS)：给定字符串A、B、C，C 称为A 和B 的最长公共子序列是指C 是A 和B 的公共子序列，且对于A 和B 的任意公共子序列D，都有D <= C 。给定字符串A 和B，A =m，B =n，不妨设m<=n，LCS 问题就是要求出A 和B 的LCS。
• 定义4 给定字符串A=A[1]A[2]…A[m]和字符串B=B[1]B[2]…[n]，A( 1:i)表示A 的连续子序列A[1]A[2]…A[i]，同样B(1:j)表示B 的连续子序列B[1]B[2]…[j]。Li(k)表示所有与字符串A(1:i) 有长度为k 的LCS 的字符串B(l:j) 中j 的最小值。用公式表示就是Li(k)=Minj(LCS(A(1:i)，B(l:j))=k) [3]。
  
  
  定理1 ∀ i∈[1，m]，有Li(l)<Li(2)<Li(3)<…<Li(m) .
  定理2 ∀i∈[l，m-1]，∀k∈[l，m]，有i 1 L + (k)<= i L (k).
  定理3 ∀ i∈[l，m-1]， ∀ k∈[l，m-l]，有i L (k)< i 1 L + (k+l).
  以上三个定理都不考虑Li(k)无定义的情况。
  定理4[3] i 1 L + (k)如果存在，那么它的取值必为: i 1 L + (k)=Min(j, i L (k))。这里j 是满足以下条件的最小整数:A[i+l]=B[j]且j> i L (k-1)。
  
  
  

   矩阵中元素L(k，i)=Li(k)，这里(1<i<=m，1<k<=m)，null 表示L(k,i)不存在。当i<k 时，显然L(k，i)不存在。
      设p=Maxk(L(k ， m) ≠ null) ， 可以证明L 矩阵中L(p,m) 所在的对角线,L(1,m-p+1),L(2,m-p+2)…L(p-1,m-1),L(p,m) 所对应的子序列B[L(1,m-p+1)]B[L(2,m-p+2)]…B[L(p,m)]即为A 和B 的LCS，p 为该LCS 的长度。这样，LCS 问题的求解就转化为对m m L × 矩阵的求解。
  
  6.2 算法思想

      根据定理,第一步求出第一行元素,L(1,1),L(1,2),…L(1,m),第二步求第二行,一直到发现第p+1 行都为null 为止。在计算过程中遇到i<k 时,L(k,i)=null, 及L(k,i)=k时,L(k,i+1)=L(k,i+2)=…L(k,m)=k。这样,计算每行的时间复杂度为O(n),则整个时间复杂度为O(pn)。在求L 矩阵的过程中不用存储整个矩阵,只需存储当前行和上一行即可。空间复杂度为O(m+n)。

      下面给出一个例子来说明:给定字符串A 和B，A=acdabbc，B=cddbacaba，(m= A =7，n= B =9)。按照定理给出的递推公式，求出A 和B 的L 矩阵如图2，其中的$表示NULL。
  
  

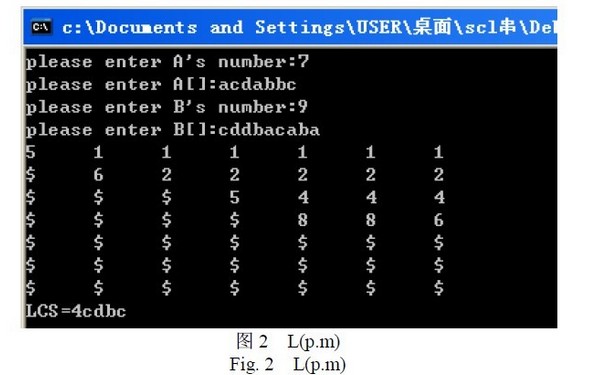
  则A 和B 的LCS 为B[1]B[2]B[4]B[6]=cdbc,LCS 的长度为4。

  6.3 算法伪代码
  算法 L(A,B,L)
  输入 长度分别为m,n 的字符串A,B
  输出 A,B 的最长公共子序列LCS

  1. L(A,B,L){//字符串A，B，所求矩阵L  
  2.   for(k=1;k<=m;k++){ //m 为A 的长度  
  3.     for(i=1;i<=m;i++){  
  4.       if(i<k) L[k][i]=N;//i<k 时,L(k,i)=null，N 代表无穷大  
  5.       if(L[k][i]==k)//L(k,i)=k 时,L(k,i+1)=L(k,i+2)=…L(k,m)=k  
  6.       for(l=i+1;l<=m;l++)  
  7.        { L[k][l]=k;  
  8.          Break;}  
  9.       for(j=1;j<=n;j++){//定理4 的实现  
  10.        if(A[i+1]==B[j]&&j>L[k-1][i]){  
  11.         L[k][i+1]=(j<L[k][i]?j:L[k][i]);  
  12.         break;  
  13.       }  
  14.       if(L[k][i+1]==0)  
  15.         L[k][i]=N;  
  16.      }  
  17.      if(L[k][m]==N)  
  18.       {p=k-1;break;}  
  19.   }  
  20.   p=k-1;  
  21. }  

  6.4 结语
      本节主要描述区别于动态规划法的一种新的求解最长公共子序列问题的方法，在不影响精确度的前提下，提高序列匹配的速度，根据定理i 1 L + (k)=Min(j, i L (k))得出矩阵，在求解矩阵的过程中对最耗时的L(p,m)进行条件约束优化。我们在Intel(R) Core(TM)2 Quad 双核处理器、1G 内存，软件环境：windows xp 下试验结果证明，本文算法与其他经典的比对算法相比,不但能够取得准确的结果,而且速度有了较大的提高（本节参考了刘佳梅女士的论文）。

      若有任何问题，恳请不吝指正。谢谢各位。完。

  
  
  

作者：July、狂想曲创作组。
出处：http://blog.csdn.net/v_JULY_v 。

前奏
    有这样一个问题：在一条左右水平放置的直线轨道上任选两个点，放置两个机器人，请用如下指令系统为机器人设计控制程序，使这两个机器人能够在直线轨道上相遇。（注意两个机器人用你写的同一个程序来控制）。
    指令系统：只包含4条指令，向左、向右、条件判定、无条件跳转。其中向左（右）指令每次能控制机器人向左（右）移动一步；条件判定指令能对机器人所在的位置进行条件测试，测试结果是如果对方机器人曾经到过这里就返回true，否则返回false；无条件跳转，类似汇编里面的跳转，可以跳转到任何地方。

    ok，这道很有意思的趣味题是去年微软工程院的题，文末将给出解答（如果急切想知道此问题的答案，可以直接跳到本文第三节）。同时，我们看到其实这个题是一个典型的追赶问题，那么追赶问题在哪种面试题中比较常见?对了，链表追赶。本章就来阐述这个问题。有不正之处，望不吝指正。

第一节、求链表倒数第k个结点
第13题、题目描述：
输入一个单向链表，输出该链表中倒数第k个结点,
链表的倒数第0个结点为链表的尾指针。

分析：此题一出，相信，稍微有点 经验的同志，都会说到：设置两个指针p1,p2，首先p1和p2都指向head，然后p2向前走k步，这样p1和p2之间就间隔k个节点，最后p1和p2同时向前移动，直至p2走到链表末尾。

    前几日有朋友提醒我说，让我讲一下此种求链表倒数第k个结点的问题。我想，这种问题，有点经验的人恐怕都已了解过，无非是利用两个指针一前一后逐步前移。但他提醒我说，如果参加面试的人没有这个意识，它怎么也想不到那里去。

    那在平时准备面试的过程中如何加强这一方面的意识呢?我想，除了平时遇到一道面试题，尽可能用多种思路解决，以延伸自己的视野之外，便是平时有意注意观察生活。因为，相信，你很容易了解到，其实这种链表追赶的问题来源于生活中长跑比赛，如果平时注意多多思考，多多积累，多多发现并体味生活，相信也会对面试有所帮助。

    ok，扯多了，下面给出这个题目的主体代码，如下：

struct ListNode
{
    char data;
    ListNode* next;
};
ListNode* head,*p,*q;
ListNode *pone,*ptwo;

//@heyaming, 第一节,求链表倒数第k个结点应该考虑k大于链表长度的case。
ListNode* fun(ListNode *head,int k)
{
 assert(k >= 0);
 pone = ptwo = head;
 for( ; k > 0 && ptwo != NULL; k--)
  ptwo=ptwo->next;
 if (k > 0) return NULL;
 
 while(ptwo!=NULL)
 {
  pone=pone->next;
  ptwo=ptwo->next;
 }
 return pone;
} 

 

扩展：
这是针对链表单项链表查找其中倒数第k个结点。试问，如果链表是双向的，且可能存在环呢?请看第二节、编程判断两个链表是否相交。

第二节、编程判断两个链表是否相交
题目描述：给出两个单向链表的头指针（如下图所示）

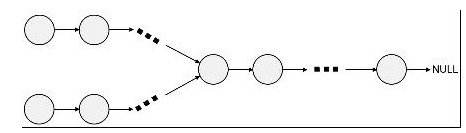
比如h1、h2，判断这两个链表是否相交。这里为了简化问题，我们假设两个链表均不带环。

分析：这是来自编程之美上的微软亚院的一道面试题目。请跟着我的思路步步深入（部分文字引自编程之美）：

1. 直接循环判断第一个链表的每个节点是否在第二个链表中。但，这种方法的时间复杂度为O(Length(h1) * Length(h2))。显然，我们得找到一种更为有效的方法，至少不能是O（N^2）的复杂度。
2. 针对第一个链表直接构造hash表，然后查询hash表，判断第二个链表的每个结点是否在hash表出现，如果所有的第二个链表的结点都能在hash表中找到，即说明第二个链表与第一个链表有相同的结点。时间复杂度为为线性：O(Length(h1) + Length(h2))，同时为了存储第一个链表的所有节点，空间复杂度为O(Length(h1))。是否还有更好的方法呢，既能够以线性时间复杂度解决问题，又能减少存储空间？
3. 进一步考虑“如果两个没有环的链表相交于某一节点，那么在这个节点之后的所有节点都是两个链表共有的”这个特点，我们可以知道，如果它们相交，则最后一个节点一定是共有的。而我们很容易能得到链表的最后一个节点，所以这成了我们简化解法的一个主要突破口。那么，我们只要判断俩个链表的尾指针是否相等。相等，则链表相交；否则，链表不相交。
   所以，先遍历第一个链表，记住最后一个节点。然后遍历第二个链表，到最后一个节点时和第一个链表的最后一个节点做比较，如果相同，则相交，否则，不相交。这样我们就得到了一个时间复杂度，它为O((Length(h1) + Length(h2))，而且只用了一个额外的指针来存储最后一个节点。这个方法时间复杂度为线性O（N），空间复杂度为O（1），显然比解法三更胜一筹。
4. 上面的问题都是针对链表无环的，那么如果现在，链表是有环的呢?还能找到最后一个结点进行判断么?上面的方法还同样有效么?显然，这个问题的本质已经转化为判断链表是否有环。那么，如何来判断链表是否有环呢?

总结：
所以，事实上，这个判断两个链表是否相交的问题就转化成了：
1.先判断带不带环
2.如果都不带环，就判断尾节点是否相等
3.如果都带环，判断一链表上俩指针相遇的那个节点，在不在另一条链表上。
如果在，则相交，如果不在，则不相交。

    1、那么，如何编写代码来判断链表是否有环呢?因为很多的时候，你给出了问题的思路后，面试官可能还要追加你的代码，ok，如下（设置两个指针(p1, p2)，初始值都指向头，p1每次前进一步，p2每次前进二步，如果链表存在环，则p2先进入环，p1后进入环，两个指针在环中走动，必定相遇）：

 

1. //copyright@ KurtWang  
2. //July、2011.05.27。  
3. struct Node  
4. {  
5.     int value;  
6.     Node * next;  
7. };  
8.   
9. //1.先判断带不带环  
10. //判断是否有环，返回bool，如果有环，返回环里的节点  
11. //思路：用两个指针，一个指针步长为1，一个指针步长为2，判断链表是否有环  
12. bool isCircle(Node * head, Node *& circleNode, Node *& lastNode)  
13. {  
14.     Node * fast = head->next;  
15.     Node * slow = head;  
16.     while(fast != slow && fast && slow)  
17.     {  
18.         if(fast->next != NULL)  
19.             fast = fast->next;  
20.           
21.         if(fast->next == NULL)  
22.             lastNode = fast;  
23.         if(slow->next == NULL)  
24.             lastNode = slow;  
25.           
26.         fast = fast->next;  
27.         slow = slow->next;  
28.           
29.     }  
30.     if(fast == slow && fast && slow)  
31.     {  
32.         circleNode = fast;  
33.         return true;  
34.     }  
35.     else  
36.         return false;  
37. }  

 

    2&3、如果都不带环，就判断尾节点是否相等，如果都带环，判断一链表上俩指针相遇的那个节点，在不在另一条链表上。下面是综合解决这个问题的代码：

 

1. //判断带环不带环时链表是否相交  
2. //2.如果都不带环，就判断尾节点是否相等  
3. //3.如果都带环，判断一链表上俩指针相遇的那个节点，在不在另一条链表上。  
4. bool detect(Node * head1, Node * head2)  
5. {  
6.     Node * circleNode1;  
7.     Node * circleNode2;  
8.     Node * lastNode1;  
9.     Node * lastNode2;  
10.       
11.     bool isCircle1 = isCircle(head1,circleNode1, lastNode1);  
12.     bool isCircle2 = isCircle(head2,circleNode2, lastNode2);  
13.       
14.     //一个有环，一个无环  
15.     if(isCircle1 != isCircle2)  
16.         return false;  
17.     //两个都无环，判断最后一个节点是否相等  
18.     else if(!isCircle1 && !isCircle2)  
19.     {  
20.         return lastNode1 == lastNode2;  
21.     }  
22.     //两个都有环，判断环里的节点是否能到达另一个链表环里的节点  
23.     else  
24.     {  
25.         Node * temp = circleNode1->next;  //updated，多谢苍狼 and hyy。  
26.         while(temp != circleNode1)    
27.         {  
28.             if(temp == circleNode2)  
29.                 return true;  
30.             temp = temp->next;  
31.         }  
32.         return false;  
33.     }  
34.       
35.     return false;  
36. }  

 

扩展2：求两个链表相交的第一个节点
思路：在判断是否相交的过程中要分别遍历两个链表，同时记录下各自长度。

    @Joshua：这个算法需要处理一种特殊情况，即：其中一个链表的头结点在另一个链表的环中，且不是环入口结点。这种情况有两种意思：1)如果其中一个链表是循环链表，则另一个链表必为循环链表，即两个链表重合但头结点不同；2)如果其中一个链表存在环(除去循环链表这种情况)，则另一个链表必在此环中与此环重合，其头结点为环中的一个结点，但不是入口结点。在这种情况下我们约定，如果链表B的头结点在链表A的环中，且不是环入口结点，那么链表B的头结点即作为A和B的第一个相交结点；如果A和B重合(定义方法时形参A在B之前)，则取B的头结点作为A和B的第一个相交结点。 

    代码如下：

    关于判断单链表是否相交的问题，还可以看看此篇文章：http://www.cppblog.com/humanchao/archive/2008/04/17/47357.html。ok，下面，回到本章前奏部分的那道非常有趣味的智力题。

第三节、微软工程院面试智力题
题目描述：
    在一条左右水平放置的直线轨道上任选两个点，放置两个机器人，请用如下指令系统为机器人设计控制程序，使这两个机器人能够在直线轨道上相遇。（注意两个机器人用你写的同一个程序来控制）
    指令系统：只包含4条指令，向左、向右、条件判定、无条件跳转。其中向左（右）指令每次能控制机器人向左（右）移动一步；条件判定指令能对机器人所在的位置进行条件测试，测试结果是如果对方机器人曾经到过这里就返回true，否则返回false；无条件跳转，类似汇编里面的跳转，可以跳转到任何地方。

分析：我尽量以最清晰的方式来说明这个问题（大部分内容来自ivan，big等人的讨论）：
      1、首先题目要求很简单，就是要你想办法让A最终能赶上B，A在后，B在前，都向右移动，如果它们的速度永远一致，那A是永远无法追赶上B的。但题目给出了一个条件判断指令，即如果A或B某个机器人向前移动时，若是某个机器人经过的点是第二个机器人曾经经过的点，那么程序返回true。对的，就是抓住这一点，A到达曾经B经过的点后，发现此后的路是B此前经过的，那么A开始提速两倍，B一直保持原来的一倍速度不变，那样的话，A势必会在|AB|/move_right个单位时间内，追上B。ok，简单伪代码如下：

start:
if(at the position other robots have not reached)
    move_right
if(at the position other robots have reached)
    move_right
    move_right
goto start

再简单解释下上面的伪代码（@big）：
A------------B
|                  |
在A到达B点前，两者都只有第一条if为真，即以相同的速度向右移动，在A到达B后，A只满足第二个if，即以两倍的速度向右移动，B依然只满足第一个if，则速度保持不变，经过|AB|/move_right个单位时间，A就可以追上B。

     2、有个细节又出现了，正如ivan所说，

if(at the position other robots have reached)
    move_right
    move_right

上面这个分支不一定能提速的。why?因为如果if条件花的时间很少，而move指令发的时间很大（实际很可能是这样），那么两个机器人的速度还是基本是一样的。

那作如何修改呢?:

start:
if(at the position other robots have not reached)
    move_right
    move_left
    move_right
if(at the position other robots have reached)
    move_right
goto start

-------

这样改后，A的速度应该比B快了。

      3、然要是说每个指令处理速度都很快，AB岂不是一直以相同的速度右移了?那到底该作何修改呢?请看：

go_step()
{
   向右
   向左
   向右
}
--------
三个时间单位才向右一步

go_2step()
{
   向右
}
------

    一个时间单向右一步向左和向右花的时间是同样的，并且会占用一定时间。 如果条件判定指令时间比移令花的时间较少的话，应该上面两种步法，后者比前者快。至此，咱们的问题已经得到解决。

作者：July。
出处：http://blog.csdn.net/v_JULY_v 。

前奏

    有关虚函数的问题层出不穷，有关虚函数的文章千篇一律，那为何还要写这一篇有关虚函数的文章呢?看完本文后，相信能懂其意义之所在。同时，原狂想曲系列已经更名为程序员编程艺术系列，因为不再只专注于“面试”，而在“编程”之上了。ok，如果有不正之处，望不吝赐教。谢谢。

第一节、一道简单的虚函数的面试题
题目要求：写出下面程序的运行结果?

    我想，这道面试题应该是考察虚函数相关知识的相对简单的一道题目了。然后，希望你碰到此类有关虚函数的面试题，不论其难度是难是易，都能够举一反三，那么本章的目的也就达到了。ok，请跟着我的思路，咱们步步深入（上面程序的输出结果为A B）。

第二节、有无虚函数的区别
      1、当上述程序中的函数p()不是虚函数，那么程序的运行结果是如何?即如下代码所示：

class A
{
public:
 void p() 
 { 
  cout << "A" << endl; 
 }
 
};

class B : public A
{
public:
 void p() 
 { 
  cout << "B" << endl;
 }
};

对的，程序此时将输出两个A，A。为什么?
我们知道，在构造一个类的对象时，如果它有基类，那么首先将构造基类的对象，然后才构造派生类自己的对象。如上，A* a=new A，调用默认构造函数构造基类A对象，然后调用函数p()，a->p();输出A，这点没有问题。
    然后，A * b = new B;，构造了派生类对象B，B由于是基类A的派生类对象，所以会先构造基类A对象，然后再构造派生类对象，但由于当程序中函数是非虚函数调用时，B类对象对函数p()的调用时在编译时就已静态确定了，所以，不论基类指针b最终指向的是基类对象还是派生类对象，只要后面的对象调用的函数不是虚函数，那么就直接无视，而调用基类A的p()函数。

      2、那如果加上虚函数呢?即如最开始的那段程序那样，程序的输出结果，将是什么?
在此之前，我们还得明确以下两点：
    a、通过基类引用或指针调用基类中定义的函数时，我们并不知道执行函数的对象的确切类型，执行函数的对象可能是基类类型的，也可能是派生类型的。
    b、如果调用非虚函数，则无论实际对象是什么类型，都执行基类类型所定义的函数（如上述第1点所述）。如果调用虚函数，则直到运行时才能确定调用哪个函数，运行的虚函数是引用所绑定的或指针所指向的对象所属类型定义的版本。

根据上述b的观点，我们知道，如果加上虚函数，如上面这道面试题，

class A
{
public:
 virtual void p() 
 { 
  cout << "A" << endl; 
 }
 
};

class B : public A
{
public:
 virtual void p() 
 { 
  cout << "B" << endl;
 }
};

int main() 
{
 A * a = new A;
 A * b = new B;
 a->p();
 b->p();
 delete a;
 delete b;
    return 0;
}

 

那么程序的输出结果将是A B。

所以，至此，咱们的这道面试题已经解决。但虚函数的问题，还没有解决。

第三节、虚函数的原理与本质
    我们已经知道，虚（virtual）函数的一般实现模型是：每一个类（class）有一个虚表（virtual table），内含该class之中有作用的虚（virtual）函数的地址，然后每个对象有一个vptr，指向虚表（virtual table）的所在。

请允许我援引自深度探索c++对象模型一书上的一个例子：

class Point { 
public: 
   virtual ~Point();  

   virtual Point& mult( float ) = 0; 

   float x() const { return _x; }     //非虚函数，不作存储
   virtual float y() const { return 0; }  
   virtual float z() const { return 0; }  
   // ...

protected: 
   Point( float x = 0.0 ); 
   float _x; 
};

      1、在Point的对象pt中，有两个东西，一个是数据成员_x，一个是_vptr_Point。其中_vptr_Point指向着virtual table point，而virtual table（虚表）point中存储着以下东西：

• virtual ~Point()被赋值slot 1，
• mult() 将被赋值slot 2.
• y() is 将被赋值slot 3
• z() 将被赋值slot 4.

class Point2d : public Point { 
public: 
   Point2d( float x = 0.0, float y = 0.0 )  
      : Point( x ), _y( y ) {} 
   ~Point2d();   //1

   //改写base class virtual functions 
   Point2d& mult( float );  //2
   float y() const { return _y; }  //3

protected: 
   float _y; 
};

      2、在Point2d的对象pt2d中，有三个东西，首先是继承自基类pt对象的数据成员_x，然后是pt2d对象本身的数据成员_y，最后是_vptr_Point。其中_vptr_Point指向着virtual table point2d。由于Point2d继承自Point，所以在virtual table point2d中存储着：改写了的其中的~Point2d()、Point2d& mult( float )、float y() const，以及未被改写的Point::z()函数。

class Point3d: public Point2d { 
public: 
   Point3d( float x = 0.0, 
            float y = 0.0, float z = 0.0 ) 
      : Point2d( x, y ), _z( z ) {} 
   ~Point3d();

   // overridden base class virtual functions 
   Point3d& mult( float ); 
   float z() const { return _z; }

   // ... other operations ... 
protected: 
   float _z; 
};

      3、在Point3d的对象pt3d中，则有四个东西，一个是_x，一个是_vptr_Point，一个是_y，一个是_z。其中_vptr_Point指向着virtual table point3d。由于point3d继承自point2d，所以在virtual table point3d中存储着：已经改写了的point3d的~Point3d()，point3d::mult()的函数地址，和z()函数的地址，以及未被改写的point2d的y()函数地址。

ok，上述1、2、3所有情况的详情，请参考下图。

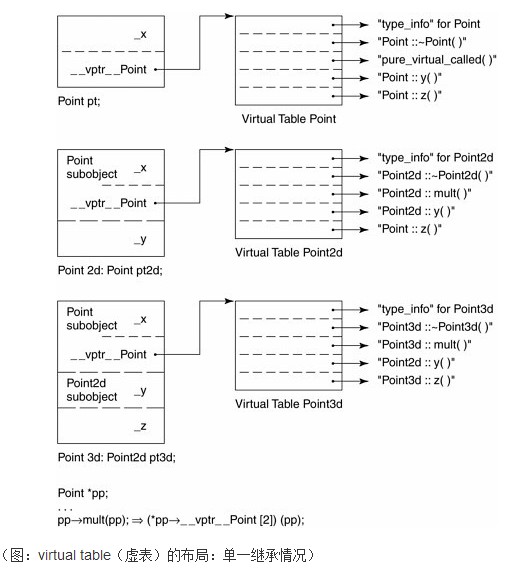
本文，日后可能会酌情考虑增补有关内容。ok，更多，可参考深度探索c++对象模型一书第四章。
最近几章难度都比较小，是考虑到狂想曲有深有浅的原则，后续章节会逐步恢复到相应难度。

第四节、虚函数的布局与汇编层面的考察

      ivan、老梦的两篇文章继续对虚函数进行了一番深入，我看他们已经写得很好了，我就不饶舌了。ok，请看：1、VC虚函数布局引发的问题，2、从汇编层面深度剖析C++虚函数、http://blog.csdn.net/linyt/archive/2011/04/20/6336762.aspx。

第五节、虚函数表的详解

    本节全部内容来自淄博的共享，非常感谢。注@molixiaogemao：只有发生继承的时候且父类子类都有virtual的时候才会出现虚函数指针，请不要忘了虚函数出现的目的是为了实现多态。
 

 一般继承（无虚函数覆盖）
 下面，再让我们来看看继承时的虚函数表是什么样的。假设有如下所示的一个继承关系：

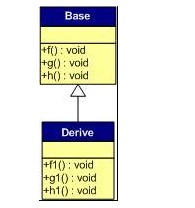
请注意，在这个继承关系中，子类没有重载任何父类的函数。那么，在派生类的实例中，

 对于实例：Derive d; 的虚函数表如下：

我们从表中可以看到下面几点，
 1）覆盖的f()函数被放到了虚表中原来父类虚函数的位置。
 2）没有被覆盖的函数依旧。
 
 这样，我们就可以看到对于下面这样的程序，
 Base *b = new Derive();

b->f();

由b所指的内存中的虚函数表的f()的位置已经被Derive::f()函数地址所取代，
于是在实际调用发生时，是Derive::f()被调用了。这就实现了多态。

多重继承（无虚函数覆盖）

下面，再让我们来看看多重继承中的情况，假设有下面这样一个类的继承关系（注意：子类并没有覆盖父类的函数）：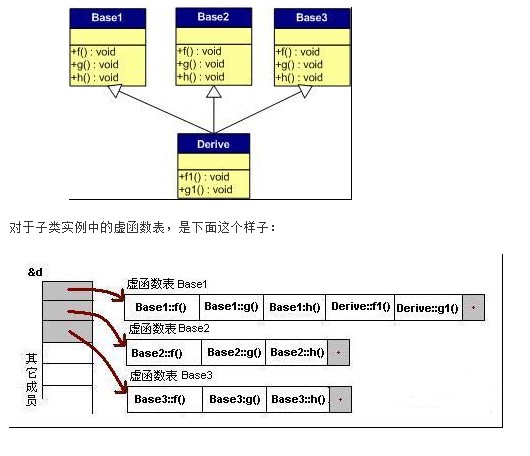

我们可以看到：
1） 每个父类都有自己的虚表。
2） 子类的成员函数被放到了第一个父类的表中。（所谓的第一个父类是按照声明顺序来判断的）

这样做就是为了解决不同的父类类型的指针指向同一个子类实例，而能够调用到实际的函数。

多重继承（有虚函数覆盖）
下面我们再来看看，如果发生虚函数覆盖的情况。
下图中，我们在子类中覆盖了父类的f()函数。

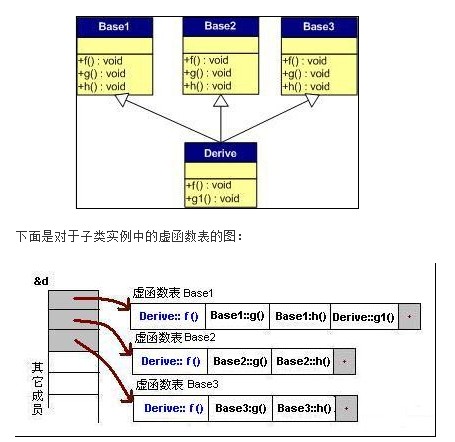
我们可以看见，三个父类虚函数表中的f()的位置被替换成了子类的函数指针。
这样，我们就可以任一静态类型的父类来指向子类，并调用子类的f()了。如：

Derive d;
Base1 *b1 = &d;
Base2 *b2 = &d;
Base3 *b3 = &d;
b1->f(); //Derive::f()
b2->f(); //Derive::f()
b3->f(); //Derive::f()
b1->g(); //Base1::g()
b2->g(); //Base2::g()
b3->g(); //Base3::g()

 

安全性
每次写C++的文章，总免不了要批判一下C++。
这篇文章也不例外。通过上面的讲述，相信我们对虚函数表有一个比较细致的了解了。
水可载舟，亦可覆舟。下面，让我们来看看我们可以用虚函数表来干点什么坏事吧。

一、通过父类型的指针访问子类自己的虚函数
我们知道，子类没有重载父类的虚函数是一件毫无意义的事情。因为多态也是要基于函数重载的。
虽然在上面的图中我们可以看到Base1的虚表中有Derive的虚函数，但我们根本不可能使用下面的语句来调用子类的自有虚函数：

Base1 *b1 = new Derive();
b1->g1(); //编译出错

任何妄图使用父类指针想调用子类中的未覆盖父类的成员函数的行为都会被编译器视为非法，即基类指针不能调用子类自己定义的成员函数。所以，这样的程序根本无法编译通过。
但在运行时，我们可以通过指针的方式访问虚函数表来达到违反C++语义的行为。
（关于这方面的尝试，通过阅读后面附录的代码，相信你可以做到这一点）

二、访问non-public的虚函数
另外，如果父类的虚函数是private或是protected的，但这些非public的虚函数同样会存在于虚函数表中，
所以，我们同样可以使用访问虚函数表的方式来访问这些non-public的虚函数，这是很容易做到的。
如：

class Base {
private: 
 virtual void f() { cout << "Base::f" << endl; } 
};

class Derive : public Base{ 
};
typedef void(*Fun)(void);
void main() {
 Derive d;
 Fun pFun = (Fun)*((int*)*(int*)(&d)+0);
 pFun(); 
}

对上面粗体部分的解释（@a && x）：

1. (int*)(&d)取vptr地址，该地址存储的是指向vtbl的指针
2. (int*)*(int*)(&d)取vtbl地址，该地址存储的是虚函数表数组
3. (Fun)*((int*)*(int*)(&d) +0)，取vtbl数组的第一个元素，即Base中第一个虚函数f的地址
4. (Fun)*((int*)*(int*)(&d) +1)，取vtbl数组的第二个元素（这第4点，如下图所示）。

下图也能很清晰的说明一些东西（@5）：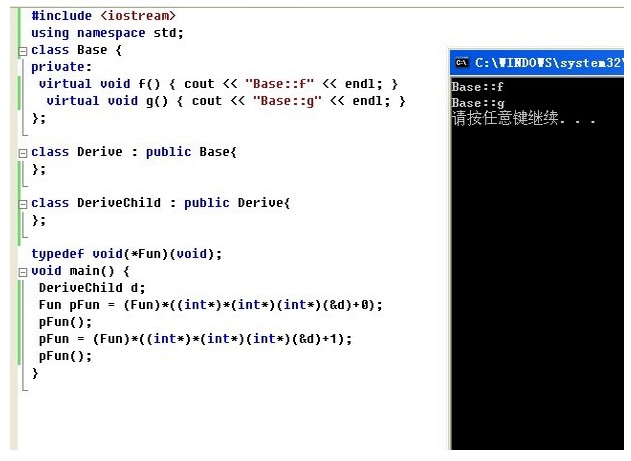

ok，再来看一个问题，如果一个子类重载的虚拟函数为privete，那么通过父类的指针可以访问到它吗？

#include <IOSTREAM>   
class B   
{    
public:    
    virtual void fun()      
    {     
        std::cout << "base fun called";     
    };    
};  

class D : public B    
{    
private:   
    virtual void fun()      
    {     
        std::cout << "driver fun called";    
    };    
};  

int main(int argc, char* argv[])   
{       
    B* p = new D();    
    p->fun();    
    return 0;    
}  
运行时会输出 driver fun called

从这个实验，可以更深入的了解虚拟函数编译时的一些特征:
在编译虚拟函数调用的时候，例如p->fun(); 只是按其静态类型来处理的, 在这里p的类型就是B，不会考虑其实际指向的类型（动态类型）。
    也就是说，碰到p->fun();编译器就当作调用B的fun来进行相应的检查和处理。
因为在B里fun是public的，所以这里在“访问控制检查”这一关就完全可以通过了。
然后就会转换成(*p->vptr[1])(p)这样的方式处理, p实际指向的动态类型是D，
    所以p作为参数传给fun后(类的非静态成员函数都会编译加一个指针参数，指向调用该函数的对象，我们平常用的this就是该指针的值）, 实际运行时p->vptr[1]则获取到的是D::fun()的地址，也就调用了该函数, 这也就是动态运行的机理。

为了进一步的实验，可以将B里的fun改为private的，D里的改为public的，则编译就会出错。
C++的注意条款中有一条" 绝不重新定义继承而来的缺省参数值" 
（Effective C++ Item37， never redefine a function's inherited default parameter value) 也是同样的道理。

可以再做个实验
class B   
{    
public:   
    virtual void fun(int i = 1)      
    {     
        std::cout << "base fun called, " << i;     
    };    
};  

class D : public B    
{    
private:    
    virtual void fun(int i = 2)      
    {     
        std::cout << "driver fun called, " << i;     
    };    
}; 

 

 

则运行会输出driver fun called, 1

 

关于这一点，Effective上讲的很清楚“virtual 函数系动态绑定， 而缺省参数却是静态绑定”，
也就是说在编译的时候已经按照p的静态类型处理其默认参数了,转换成了(*p->vptr[1])(p, 1)这样的方式。 

补遗

   一个类如果有虚函数，不管是几个虚函数，都会为这个类声明一个虚函数表，这个虚表是一个含有虚函数的类的，不是说是类对象的。一个含有虚函数的类，不管有多少个数据成员，每个对象实例都有一个虚指针，在内存中，存放每个类对象的内存区，在内存区的头部都是先存放这个指针变量的（准确的说，应该是：视编译器具体情况而定），从第n（n视实际情况而定）个字节才是这个对象自己的东西。

 

下面再说下通过基类指针，调用虚函数所发生的一切：
One *p;
p->disp();

1、上来要取得类的虚表的指针，就是要得到，虚表的地址。存放类对象的内存区的前四个字节其实就是用来存放虚表的地址的。
2、得到虚表的地址后，从虚表那知道你调用的那个函数的入口地址。根据虚表提供的你要找的函数的地址。并调用函数；你要知道，那个虚表是一个存放指针变量的数组，并不是说，那个虚表中就是存放的虚函数的实体。

本章完。

 程序员编程艺术：第七章、求连续子数组的最大和 

作者：July。
出处：http://blog.csdn.net/v_JULY_v 。

前奏

• 希望更多的人能和我一样，把本狂想曲系列中的任何一道面试题当做一道简单的编程题或一个实质性的问题来看待，在阅读本狂想曲系列的过程中，希望你能尽量暂时放下所有有关面试的一切包袱，潜心攻克每一道“编程题”，在解决编程题的过程中，好好享受编程带来的无限乐趣，与思考带来的无限激情。--By@July_____。
• 原狂想曲系列已更名为：程序员编程艺术系列。原狂想曲创作组更名为编程艺术室。编程艺术室致力于以下三点工作：1、针对一个问题，不断寻找更高效的算法，并予以编程实现。2、解决实际中会碰到的应用问题，如第十章、如何给10^7个数据量的磁盘文件排序。3、经典算法的研究与实现。总体突出一点：编程，如何高效的编程解决实际问题。欢迎有志者加入。

第一节、求子数组的最大和
3.求子数组的最大和
题目描述：
输入一个整形数组，数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。

例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5，和最大的子数组为3, 10, -4, 7, 2，
因此输出为该子数组的和18。

分析：这个问题在各大公司面试中出现频率之频繁，被人引用次数之多，非一般面试题可与之匹敌。单凭这点，就没有理由不入选狂想曲系列中了。此题曾作为本人之前整理的微软100题中的第3题，至今反响也很大。ok，下面，咱们来一步一步分析这个题：
      1、求一个数组的最大子数组和，如此序列1, -2, 3, 10, -4, 7, 2, -5，我想最最直观也是最野蛮的办法便是，三个for循环三层遍历，求出数组中每一个子数组的和，最终求出这些子数组的最大的一个值。
记Sum[i, …, j]为数组A中第i个元素到第j个元素的和（其中0 <= i <= j < n），遍历所有可能的Sum[i, …, j]，那么时间复杂度为O（N^3）：

//本段代码引自编程之美
int MaxSum(int* A, int n)
{
 int maximum = -INF; 
 int sum=0;   
 for(int i = 0; i < n; i++)
 {
  for(int j = i; j < n; j++)
  {
   for(int k = i; k <= j; k++)
   {
    sum += A[k];
   }
   if(sum > maximum)
    maximum = sum;

   sum=0;   //这里要记得清零，否则的话sum最终存放的是所有子数组的和。也就是编程之美上所说的bug。多谢苍狼。
  }
 }
 return maximum;
} 

      2、其实这个问题，在我之前上传的微软100题，答案V0.2版[第1-20题答案]，便直接给出了以下O（N）的算法：

      3、不少朋友看到上面的答案之后，认为上述思路2的代码，没有处理全是负数的情况，当全是负数的情况时，我们可以让程序返回0，也可以让其返回最大的那个负数，下面便是前几日重写的，修改后的处理全是负数情况（返回最大的负数）的代码：

      4、DP解法的具体方程：@ flyinghearts：设sum[i] 为前i个元素中，包含第i个元素且和最大的连续子数组，result 为已找到的子数组中和最大的。对第i+1个元素有两种选择：做为新子数组的第一个元素、放入前面找到的子数组。
sum[i+1] = max(a[i+1], sum[i] + a[i+1])
result = max(result, sum[i])
 

扩展：
1、如果数组是二维数组，同样要你求最大子数组的和列?
2、如果是要你求子数组的最大乘积列?
3、如果同时要求输出子段的开始和结束列?

第二节、Data structures and Algorithm analysis in C

下面给出《Data structures and Algorithm analysis in C》中4种实现。

本章完。

作者：上善若水、July、yansha。
出处：http://blog.csdn.net/v_JULY_v 。

前奏
    本章陆续开始，除了继续保持原有的字符串、数组等面试题之外，会有意识的间断性节选一些有关数字趣味小而巧的面试题目，重在突出思路的“巧”，和“妙”。本章亲和数问题之关键字，“500万”，“线性复杂度”。

第一节、亲和数问题
题目描述：
求500万以内的所有亲和数
如果两个数a和b，a的所有真因数之和等于b,b的所有真因数之和等于a,则称a,b是一对亲和数。
例如220和284，1184和1210，2620和2924。

分析：
    首先得明确到底是什么是亲和数?

亲和数问题最早是由毕达哥拉斯学派发现和研究的。他们在研究数字的规律的时候发现有以下性质特点的两个数：
220的真因子是：1、2、4、5、10、11、20、22、44、55、110；
284的真因子是：1、2、4、71、142。
而这两个数恰恰等于对方的真因子各自加起来的和（sum[i]表示数i 的各个真因子的和），即
220=1+2+4+71+142=sum[284],
284=1+2+4+5+10+11+20+22+44+55+110=sum[220]。
得284的真因子之和sum[284]=220，且220的真因子之和sum[220]=284，即有sum[220]=sum[sum[284]]=284。

如此，是否已看出丝毫端倪?

如上所示，考虑到1是每个整数的因子，把出去整数本身之外的所有因子叫做这个数的“真因子”。如果两个整数，其中每一个真因子的和都恰好等于另一个数，那么这两个数，就构成一对“亲和数”（有关亲和数的更多讨论，可参考这：http://t.cn/hesH09）。

求解：
    了解了什么是亲和数，接下来咱们一步一步来解决上面提出的问题（以下内容大部引自水的原话，同时水哥有一句原话，“在你真正弄弄懂这个范例之前，你不配说你懂数据结构和算法”）。

1. 看到这个问题后，第一想法是什么？模拟搜索+剪枝？回溯？时间复杂度有多大？其中bn为an的伪亲和数，即bn是an的真因数之和大约是多少？至少是10^13（@iicup：N^1.5 对于5*10^6 , 次数大致 10^10 而不是 10^13.）的数量级的。那么对于每秒千万次运算的计算机来说，大概在1000多天也就是3年内就可以搞定了（iicup的计算: 10^13 / 10^7 =1000000(秒) 大约 278 小时. ）。如果是基于这个基数在优化，你无法在一天内得到结果的。
2. 一个不错的算法应该在半小时之内搞定这个问题，当然这样的算法有很多。节约时间的做法是可以生成伴随数组，也就是空间换时间，但是那样，空间代价太大，因为数据规模庞大。
3. 在稍后的算法中，依然使用的伴随数组，只不过，因为题目的特殊性，只是它方便和巧妙地利用了下标作为伴随数组，来节约时间。同时，将回溯的思想换成递推的思想（预处理数组的时间复杂度为logN（调和级数）*N，扫描数组的时间复杂度为线性O（N）。所以，总的时间复杂度为O（N*logN+N）（其中logN为调和级数）  ）。

第二节、伴随数组线性遍历
依据上文中的第3点思路，编写如下代码：

第三节、程序的构造与解释
    我再来具体解释下上述程序的原理，ok，举个例子，假设是求10以内的亲和数，求解步骤如下：

因为所有数的真因数都包含1，所以，先在各个数的下方全部置1

1. 然后取i=2,3,4,5（i<=10/2），j依次对应的位置为j=（4、6、8、10），（6、9）,（8）,（10）各数所对应的位置。
2. 依据j所找到的位置，在j所指的各个数的下面加上各个真因子i（i=2、3、4、5）。
   整个过程，即如下图所示（如sum[6]=1+2+3=6，sum[10]=1+2+5=8.）：
   1  2  3  4  5  6  7  8  9  10
   1  1  1  1  1  1  1  1  1  1
              2      2      2      2
                      3          3 
                              4
                                      5
3. 然后一次遍历i从220开始到5000000，i每遍历一个数后，
   将i对应的数下面的各个真因子加起来得到一个和sum[i]，如果这个和sum[i]==某个i’，且sum[i‘]=i，
   那么这两个数i和i’，即为一对亲和数。
4. i=2；sum[4]+=2，sum[6]+=2，sum[8]+=2，sum[10]+=2，sum[12]+=2...
   i=3，sum[6]+=3，sum[9]+=3...
   ......
5. i=220时，sum[220]=284，i=284时，sum[284]=220；即sum[220]=sum[sum[284]]=284，
   得出220与284是一对亲和数。所以，最终输出220、284，...

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

最小二乘法原理

在我们研究两个变量(x, y)之间的相互关系时，通常可以得到一系列成对的数据( x₁, y₁.  x₂, y₂.  …    x_m , y_m )；将这些数据描绘在x -y直角坐标系中，若发现这些点在一条直线附近，可以令这条直线方程如(式1-1)。

Y_计= a₀ + a₁ X                      (式1-1)

其中：a₀、a₁ 是任意实数

为建立这直线方程就要确定a₀和a₁，应用 最小二乘法原理 ，将实测值Y_i与利用(式1-1)计算值(Y_计=a₀+a₁X)的离差(Y_i-Y_计)的平方和〔∑(Y_i - Y_计)²〕最小为“优化判据”。

令： φ = ∑(Y_i - Y_计)²                 (式1-2)

把(式1-1)代入(式1-2)中得:

φ = ∑(Y_i - a₀ - a₁ X_i)²                (式1-3)

当∑(Y_i-Y_计)平方最小时，可用函数 φ 对a₀、a₁求偏导数，令这两个偏导数等于零。

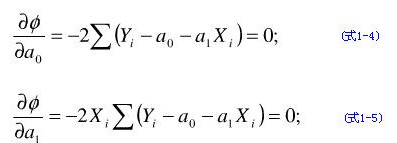
亦即：

m a₀ + (∑X_i ) a₁ = ∑Y_i                          (式1-6)

(∑X_i ) a₀ + (∑X_i² ) a₁ = ∑(X_i, Y_i)                    (式1-7)

得到的两个关于a₀、 a₁为未知数的两个方程组，解这两个方程组得出：

a₀ = (∑Y_i) / m - a₁(∑X_i) / m                             (式1-8)

a₁ = [m∑X_i Y_i - (∑X_i ∑Y_i)] / [m∑X_i² - (∑X_i)² )]                 (式1-9)

这时把a₀、a₁代入(式1-1)中， 此时的(式1-1)就是我们回归的元线性方程即：数学模型。

在回归过程中，回归的关联式是不可能全部通过每个回归数据点( x₁, y₁.  x₂, y₂.  …    x_m , y_m ),为了判断关联式的好坏，可借助相关系数“R”，统计量“F”，剩余标准偏差“S”进行判断；“R”越趋近于 1 越好；“F”的绝对值越大越好；“S”越趋近于 0 越好。

R = [∑X_iY_i - m (∑X_i / m)(∑Y_i / m)]/ SQR{[∑X_i² - m (∑X_i / m)²][∑Y_i² - m (∑Y_i / m)²]}        (式1-10) *

在(式1-1)中，m为样本容量，即实验次数；X_i、Y_i分别任意一组实验X、Y的数值。

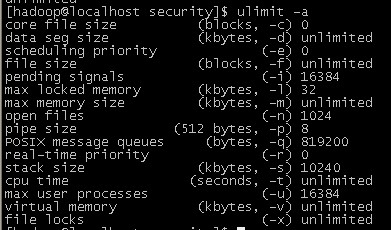一般情况下是1024，我们也可以通过ulimit –n命令来查看最大文件打开数，如下：

1024

2、  修改目标

我们的目标是：让每一个用户登录系统后系统打开的最大文件数都是我们设定好的。

但我这里不得不说的是：非常遗憾，网上很多这方面关于ulimit设置修改资源限制的文章，但没一篇文章管用。

把这个目标分解为两个目标：

2.1、设置对root用户登录系统生效

这个目标可以实现起来不难

2.2、设置对所有用户生效

这个就非常麻烦了，弄不好还会把你的系统给整坏，因为要重编译Linux的内核才行！

所以权衡之下，我只实现了第一个目标，因为第二个目标的风险太大，我想如果我之前知道这点，那么我在装系统的时候我会先做这个处理，但现在我觉得已经晚了。

3、  修改的地方

3.1、修改/etc/security/limits.conf

通过 vi /etc/security/limits.conf修改其内容，在文件最后加入（数值也可以自己定义）：

* soft  nofile = 32768

* hard  nofile = 65536

3.2、修改/etc/profile

通过vi /etc/profile修改，在最后加入以下内容

ulimit -n 32768

然后重新登录即可生效了。

说明：

其实只修改/etc/profile就可以生效了，但我还是建议把/etc/security/limits.conf也修改一下。

最后强调的是，你如果要使得修改对所有用户都生效，那么现在看来你只能重新编译Linux的内核才行。

转自：http://www.zihou.me/html/2010/06/12/2281.html