路 - C++博客

文章来源:http://www.cnblogs.com/heqile/archive/2011/12/08/2280120.html

posted @ 2011-12-08 15:55 Barryhe 阅读(704) | 评论 (0) | 编辑收藏

[导入]数据结构与算法分析学习笔记(一)--二叉树的遍历(非递归)

题目来自《数据结构题集(C语言版)》,如下:

6.37 试利用栈的基本操作写出先序遍历(二叉树)的非递归算法.

----------------------------------------------------------

先序遍历,就是以结点,左子树,右子树的顺序遍历二叉树.观察并仿照其递归算法执行过程中的状态变化情况.因为是先序遍历,我们在将结点入栈前就可以访问它.如果它不是树叶,那么就优先将非空的左孩子入栈,否则入右孩子.而如果它是树叶,我们甚至不用将它入栈了.但我们要判断它是不是栈顶元素的左孩子并且这个栈顶元素还有个右孩子,如果是这样的话,我们就要将这个右孩子入栈,以保证不拉下每一个孩子:) 自己的算法如下:

1 void PreOrder_Nonrecursive(Bitree t)
2 {
3     if(!t)return;
4     InitStack(S);
5     do
6     {
7         visit(t);//访问t
8         if(!t->left&&!t->right)//树叶
9         {
10             while(!StackEmpty(S))//栈空时结束
11             {
12                 if(GetTop(S,p)&&p->right&&p->right!=t)//树叶是栈顶元素的左孩子,栈顶元素有右孩子
13                 {
14                     t=p->right;
15                     break;
16                 }
17                 Pop(S,t);//出栈,往树根攀登
18             }
19         }
20         else//不是树叶
21         {
22             Push(S,t);//入栈
23             t=(t->left)?t->left:t->right;//左孩子优先
24         }
25     }while(!StackEmpty(S));//栈空时结束
26 }

接下来

6.38 同6.37题条件,写出后序遍历的非递归算法(提示:为分辨后序遍历时两次进栈的不同返回点,需在指针进栈时同时将一个标志进栈).

----------------------------------------------------------

括号里面的提示搞的我的头很大,首先不知道它什么意思,然后自己想到一个没用什么标志的算法又害怕会不会是错的啊,半天不敢动笔,对自己很不自信啊,小悲剧.写完之后测试没什么错才放心,后来看了别的参考答案才知道那个使用标志的算法,确实很有用,那就是真正的”仿照其递归算法执行过程中的状态变化情况”,是很有意义的.以后如果遇到需要将递归转换为非递归的情况,可以认真观察递归算法的执行流程再加以仿照,也许效率会高一些.

后序遍历,就是以左子树,右子树,结点的顺序遍历二叉树.因为是后序遍历,所以我们在栈顶元素出栈的时候访问它.那么和先序遍历一样,如果栈顶元素不是树叶,那么就优先将其非空的左孩子入栈,否则入右孩子.而如果栈顶元素是树叶,那么它肯定要出栈了.同时,如果它是新的栈顶元素的左孩子,那么说明我们左子树已经访问完了,该访问右子树了(将新的栈顶元素的右孩子入栈);如果它是新的栈顶元素的右孩子,那我们右子树也访问完了,可以访问结点了(将新的栈顶元素出栈并访问它,继续这样判断).自己的算法如下:

1 void postorder_traversal(BitTree t)
2 {
3     if(!t)return;
4     InitStack(S);
5     Push(S,t);
6     while(!StackEmpty(S))
7     {
8         GetTop(S,t);
9         if(!t->left&&!t->right)
10         {
11             visit(t);
12             Pop(S,t);
13             while(!StackEmpty(S))
14             {
15                 GetTop(S,p);
16                 if(t==p->left&&p->right)
17                 {
18                     Push(S,p->right);
19                     break;
20                 }
21                 else
22                 {
23                     GetTop(S,t);
24                     visit(t);
25                     Pop(S,t);
26                 }
27             }
28         }
29         else
30         {
31             t=(t->left)?t->left:t->right;
32             Push(S,t);
33         }
34     }
35 }

写完之后,用C++实现了一下:

View Code

  1 // ds_c_ex_6.37.cpp : 定义控制台应用程序的入口点。
  2 //
  3
  4 #include "stdafx.h"
  5 #include <iostream>
  6 #include <vector>
  7 using namespace std;
  8
  9 struct node
10 {
11     char data;
12     node *left;
13     node *right;
14     node(char c=0,node *l=NULL,node *r=NULL):data(c),left(l),right(r){}
15 };
16
17 typedef node * BitTree;
18
19 char ch;
20
21 void CreateTree(BitTree &T)//构造二叉树(按先序次序输入)
22 {
23     ch=cin.get();
24     if(ch==' ')T=NULL;//空结点输入空格
25     else
26     {
27         T=new node(ch);
28         CreateTree(T->left);
29         CreateTree(T->right);
30     }
31     return;
32 }
33
34 void PreOrder_Nonrecursive(BitTree t)//非递归的先序遍历
35 {
36     if(!t)return;
37     vector<BitTree> S;
38     do
39     {
40         cout<<t->data<<" ";
41         if(!t->left&&!t->right)//->的优先级高于!高于&&
42         {
43             while(!S.empty())
44             {
45                 if(S.back()->right&&S.back()->right!=t)
46                 {
47                     t=S.back()->right;
48                     break;
49                 }
50                 t=S.back();
51                 S.pop_back();
52             }
53         }
54         else
55         {
56             S.push_back(t);
57             t=(t->left)?t->left:t->right;
58         }
59     }while(!S.empty());
60     cout<<endl;
61 }
62
63 void postorder_traversal(BitTree t)//非递归的后序遍历
64 {
65     if(!t)return;
66     vector<BitTree> S;
67     S.push_back(t);
68     while(!S.empty())
69     {
70         if(!S.back()->left&&!S.back()->right)
71         {
72             t=S.back();
73             cout<<t->data<<" ";
74             S.pop_back();
75             while(!S.empty())
76             {
77                 if(t==S.back()->left&&S.back()->right)
78                 {
79                     S.push_back(S.back()->right);
80                     break;
81                 }
82                 else
83                 {
84                     t=S.back();
85                     cout<<t->data<<" ";
86                     S.pop_back();
87                 }
88             }
89         }
90         else
91         {
92             t=(S.back()->left)?S.back()->left:S.back()->right;
93             S.push_back(t);
94         }
95     }
96     cout<<endl;
97 }
98
99
100
101 int _tmain(int argc, _TCHAR* argv[])
102 {
103     BitTree root=new node;
104     CreateTree(root);
105     PreOrder_Nonrecursive(root);
106     postorder_traversal(root);
107     system("PAUSE");
108     return 0;
109 }

作者: Barryhe 发表于 2011-11-16 00:30 原文链接

评论: 0　查看评论　发表评论

最新新闻：
· Google雅虎等呼吁欧盟勿制订过于严格隐私法律(2011-11-28 21:06)
· 强龙难压地头蛇微软WP7俄罗斯忍痛割Bing(2011-11-28 20:27)
· 奇艺启动新域名背后：解决视听许可证遗留问题(2011-11-28 20:25)
· Kindle“黑色星期五”销量达去年同期四倍(2011-11-28 20:24)
· 维基解密本周将启动新在线系统(2011-11-28 20:21)

编辑推荐：如何快速成为Javascript高手的思考

文章来源:http://www.cnblogs.com/heqile/archive/2011/11/16/2250506.html

posted @ 2011-11-28 21:57 Barryhe 阅读(381) | 评论 (0) | 编辑收藏

[导入]C++实践笔记(四)----AVL树的简单实现

关于AVL树的分析,请见:数据结构与算法分析学习笔记(二)--AVL树的算法思路整理

这里给出AVL树的结构定义以及insert,remove和print三种操作的例程:

  1 #include <iostream>
  2 #include <list>
  3 #include <utility>
  4 #include <string>
  5 using namespace std;
  6
  7 static const string PRINT_SPACES ="  ";
  8
  9 template <typename Object>
10 class AVLTree
11 {
12 public:
13     AVLTree(){root=NULL;}
14
15     void insert(const Object &x)
16     {insert(x,root);}
17     void remove(const Object &x)
18     {remove(x,root);}
19
20     void print();
21
22 private:
23     struct AVLnode
24     {
25         Object data;
26         AVLnode *left;
27         AVLnode *right;
28         int height;
29
30         AVLnode(Object ob,AVLnode *l,AVLnode *r,int h=0):data(ob),left(l),right(r),height(h){}
31     };
32
33     AVLnode *root;
34
35     void insert(const Object &x,AVLnode * &t);
36
37     void remove(const Object &x,AVLnode *&t);
38
39     void leftSingleRotation(AVLnode * &t);
40     void rightSingleRotation(AVLnode * &t);
41
42     void leftDoubleRotation(AVLnode * &t);
43     void rightDoubleRotation(AVLnode * &t);
44
45     int height(AVLnode * &t)
46     {
47         //结点的高度,空结点的高度为-1
48         return t==NULL?-1:t->height;
49     }
50
51     int max(int a,int b)
52     {
53         return a<b?b:a;
54     }
55
56     int powerOf2(int x)//求2的x次方(x大于等于0)
57     {
58         if(x==0)return 1;
59         int m=1;
60         while(--x>=0)
61             m*=2;
62         return m;
63     }
64
65     AVLnode * max_node(AVLnode * t)//max和min使用递归的话不能使用引用形参,不能返回引用
66     {
67         if(!t)
68             return NULL;
69         if(t->right)
70             return max_node(t->right);
71         else
72             return t;
73     }
74
75     AVLnode * min_node(AVLnode * t)
76     {
77         if(t)//考虑一下t为空的情况,使其更全面,毕竟这个函数是可以加一个public版本的重载供用户使用
78             while(t->left)
79                 t=t->left;
80         return t;
81     }
82 };
83
84 template <typename Object>
85 void AVLTree<Object>::insert(const Object &x,AVLnode * &t)
86 {
87     if(!t)
88         t=new AVLnode(x,NULL,NULL);
89     else if(x<t->data)
90     {
91         insert(x,t->left);
92         if(height(t->left)-height(t->right)==2)//在左子树插入结点后,不可能右子树比左子树高2
93             if(x<t->left->data)
94                 leftSingleRotation(t);//左单旋转
95             else
96                 leftDoubleRotation(t);//左双旋转
97         else//不需要调整就满足平衡条件的话,只需要重新计算其高度就好
98             t->height=max(height(t->left),height(t->right))+1;
99     }
100     else if(x>t->data)
101     {
102         insert(x,t->right);
103         if(height(t->right)-height(t->left)==2)
104             if(x>t->right->data)
105                 rightSingleRotation(t);//右单旋转
106             else
107                 rightDoubleRotation(t);//右双旋转
108         else
109             t->height=max(height(t->left),height(t->right))+1;
110     }
111     else;//不考虑重复的值
112 }
113
114 template <typename Object>
115 void AVLTree<Object>::leftSingleRotation(AVLnode * &t)//左单旋转
116 {
117     AVLnode *s=t->left;
118     t->left=s->right;
119     s->right=t;
120     t->height=max(height(t->left),height(t->right))+1;//重新计算s和t的高度
121     s->height=max(height(s->left),t->height)+1;
122     t=s;
123 }
124
125 template <typename Object>
126 void AVLTree<Object>::rightSingleRotation(AVLnode * &t)
127 {
128     AVLnode *s=t->right;
129     t->right=s->left;
130     s->left=t;
131     t->height=max(height(t->left),height(t->right))+1;
132     s->height=max(t->height,height(s->right))+1;
133     t=s;
134 }
135
136 template <typename Object>
137 void AVLTree<Object>::leftDoubleRotation(AVLnode * &t)//左双旋转
138 {
139     AVLnode *p=t->left;
140     AVLnode *q=p->right;
141     t->left=q->right;
142     p->right=q->left;
143     q->left=p;
144     q->right=t;
145     t->height=max(height(t->left),height(t->right))+1;//重新计算3个结点的高度
146     p->height=max(height(p->left),height(p->right))+1;
147     q->height=max(p->height,t->height)+1;
148     t=q;
149 }
150
151 template <typename Object>
152 void AVLTree<Object>::rightDoubleRotation(AVLnode * &t)
153 {
154     AVLnode *p=t->right;
155     AVLnode *q=p->left;
156     t->right=q->left;
157     p->left=q->right;
158     q->right=p;
159     q->left=t;
160     t->height=max(height(t->left),height(t->right))+1;
161     p->height=max(height(p->left),height(p->right))+1;
162     q->height=max(t->height,p->height)+1;
163     t=q;
164 }
165
166 template <typename Object>
167 void AVLTree<Object>::remove(const Object &x,AVLnode *&t)
168 {
169     if(!t)return;//没有找到要删除的值,do nothing
170     if(x<t->data)
171     {
172         remove(x,t->left);
173         if(height(t->right)-height(t->left)==2)
174         {
175             //右子树比左子树高2,那么在删除操作之前右子树比左子树高1,
176             //也就是说t的右子树必然不为空,甚至必然有非空子树(高度至少为1).
177             AVLnode *s=t->right;
178             if(height(s->left)>height(s->right))
179                 rightDoubleRotation(t);//右双旋转
180             else
181                 rightSingleRotation(t);//右单旋转
182         }
183         else
184             //不需要调整就满足平衡条件的话,只需要重新计算其高度就好
185             t->height=max(height(t->left),height(t->right))+1;
186     }
187     else if(x>t->data)
188     {
189         remove(x,t->right);
190         if(height(t->left)-height(t->right)==2)
191         {
192             AVLnode *s=t->left;
193             if(height(s->right)>height(s->left))
194                 leftDoubleRotation(t);//左双旋转
195             else
196                 leftSingleRotation(t);//左单旋转
197         }
198         else
199             t->height=max(height(t->left),height(t->right))+1;
200     }
201     else
202     {
203         if(t->left&&t->right)
204         //t的左右子树都非空,把remove操作转移到只有一个非空子树的结点或者叶子结点上去
205         {
206             if(height(t->left)>height(t->right))
207             //把remove操作往更高的那颗子树上转移
208             {
209                 //左子树中的最大值
210                 t->data=max_node(t->left)->data;
211                 remove(t->data,t->left);
212             }
213             else
214             {
215                 //右子树中的最小值
216                 t->data=min_node(t->right)->data;
217                 remove(t->data,t->right);
218             }
219         }
220         else
221         {
222             AVLnode *oldnode=t;
223             t=t->left?t->left:t->right;
224             delete oldnode;
225         }
226     }
227 }
228
229 //使用队列层次遍历打印树
230 template <typename Object>
231 void AVLTree<Object>::print()
232 {
233     if(!root)return;
234     list<pair<AVLnode *,int> > lis;//int是标志位,0表示正常值,-1表示此处没有值,应打印空格
235     lis.push_back(make_pair(root,0));
236     AVLnode *em=new AVLnode(0,NULL,NULL);//一个空的点
237     int count=1,j=0;//count表示当前行的最大结点数,j表示当前行已打印的结点数(空结点也计数)
238     int hg=root->height;//当前行的高度,计算空格时使用
239
240     while(hg>=0)//当hg<0时说明最后一行(树叶)已经打印完毕
241     {
242         while(j++!=count)
243         {
244             for(int i=1;i<powerOf2(hg);i++)
245                 cout<<PRINT_SPACES;//打印前一部分空格
246             if(lis.front().second==0)
247                 cout<<lis.front().first->data;
248             else
249                 cout<<PRINT_SPACES;//int位为-1,则打印空格以对齐
250             if(lis.front().first->left)//左子树入队
251                 lis.push_back(make_pair(lis.front().first->left,0));
252             else
253                 lis.push_back(make_pair(em,-1));
254             if(lis.front().first->right)//右子树入队
255                 lis.push_back(make_pair(lis.front().first->right,0));
256             else
257                 lis.push_back(make_pair(em,-1));
258             for(int i=0;i<powerOf2(hg);i++)
259                 cout<<PRINT_SPACES;//打印后一部分空格
260             lis.pop_front();
261         }
262         j=0;
263         count*=2;//下一行的最大节点数是上一行的两倍
264         --hg;//高度减1
265         cout<<endl;    //换行
266     }
267     delete em;
268     lis.clear();
269 }

作者: Barryhe 发表于 2011-11-28 16:30 原文链接

评论: 0　查看评论　发表评论

最新新闻：
· Google雅虎等呼吁欧盟勿制订过于严格隐私法律(2011-11-28 21:06)
· 强龙难压地头蛇微软WP7俄罗斯忍痛割Bing(2011-11-28 20:27)
· 奇艺启动新域名背后：解决视听许可证遗留问题(2011-11-28 20:25)
· Kindle“黑色星期五”销量达去年同期四倍(2011-11-28 20:24)
· 维基解密本周将启动新在线系统(2011-11-28 20:21)

编辑推荐：如何快速成为Javascript高手的思考

文章来源:http://www.cnblogs.com/heqile/archive/2011/11/28/2266385.html

posted @ 2011-11-28 21:57 Barryhe 阅读(263) | 评论 (0) | 编辑收藏

[导入]数据结构与算法分析学习笔记(二)--AVL树的算法思路整理

看完了《数据结构与算法分析(C++描述)》的4.4节AVL树,做一个总结,整理一下自己实现删除算法的思路.(注:本文中图片均来自《数据结构与算法分析(C++描述)》)

AVL(Adelson-Velskii and Landis,由阿德尔森一维尔斯和兰迪斯在1962年提出,因此得名)树是带有平衡条件(balance condition)的二叉查找树.

我们知道空子树的高度通常被定义为-1,叶子结点的高度为0,其它结点的高度为其左右子树中的最大高度加1.一颗AVL树中的每一个结点的左子树和右子树的高度差不超过1.由此,我们可以考察一下一颗高度为h的AVL树的最少结点数S(h).显然S(0)=1,S(1)=2,而S(2)=S(0)+S(1)+1=3.由数学归纳法可以证明S(h)=S(h-1)+S(h-2)+1.

AVL树的优势显而易见,它能更快的进行查找.那么怎样形成并保持一颗AVL树呢?首先我们来看insert(插入)操作.假设我们向一颗空的AVL树中按顺序插入1,2,3这3个数.1是根,2是1的右子树,3是2的右子树,这时我们发现1已经不满足平衡条件了,它的左子树高度为-1,而右子树高度为1.当遇到这种情况时,我们要立即进行某种操作使得不满足平衡条件的结点重新满足平衡条件.通过画图分析,可得在insert操作中,出现一个结点t不满足平衡条件可能出现在下面4种情况中:

(1)在t的左儿子的左子树中进行一次插入.(例如:3,2,1)

(2)在t的左儿子的右子树中进行一次插入.(例如:3,1,2)

(3)在t的右儿子的左子树中进行一次插入.(例如:1,3,2)

(4)在t的右儿子的右子树中进行一次插入.(例如:1,2,3)

注意,上面举得例子只是最简单的的例子,我们应该多插入一些结点需找规律.这种寻找”测试数据”的能力也是必不可少的,以后自己要多加注意.课本上给出了一个不长但很有价值的例子.从初始为空的AVL树开始插入项3,2和1,然后依序插入4到7.

当插入1时,根结点3不满足平衡条件,这时情况比较简单,我们自然会想到让2作为根,而1和3分别作为2的左右子树.那么继续插入,当插入5时,结点3出现了不平衡,同样我们想到让4取代3的位置,而3和5分别作为4的左右子树.

当插入6时,我们发现2不满足平衡条件,这时我们按照刚才的思路,试着让4取代2的位置,而2作为4的左儿子,2的左子树和4的右子树不变.最后我们注意到4的左子树中结点的值一定大于2且小于4,因此将原来4的左子树移到新的2结点的右子树.

由以上分析,我们可以得到情况(1)和(4)的解决方法.以情况(1)为例,如下图的左边部分,k1是k2的左儿子,在k1的左子树插入一个结点后使得k2不满足平衡条件.可以这样推理:

k2出现不平衡

->k2的左子树比右子树高2

->k1的高度本就比Z高1,现在又提高了1;又k1在其左子树X中插入结点后依然满足平衡条件的且其高度增加了1

->X,Y,Z原本一样高;在X中插入结点使得X本身高度加1.

得到这些子树的高度关系后,我们就可以通过”旋转”使得k2重新满足平衡条件.我们将Y先拿掉,将k1和k2对调(k1的左子树X和k2的右子树Z依然跟着它们),最后再根据查找树的性质,将Y作为k2的右子树,这样k1和k2就都满足了平衡条件.这种操作可以叫做左单旋转.注意,这样一来,这整个一颗树的高度在插入前和插入并旋转后没有发生变化,因此必然不会影响它的父节点(如果存在的话)的平衡情况.也就是说,对于情况(1)和(4),一次insert操作最多只需要一次的旋转操作就可以使整颗AVL树保持平衡.事实上,我们将看到情况(2)和(3)也是这样.

接下来,我们来看情况(2).如下图,k1的右子树Y在进行一次插入操作后比X高1使得k2不满足平衡条件.这时如果我们按照上面的方法进行旋转会发现只是从情况(2)变成情况(3).

继续在纸上画图,既然k1的右子树Y进行了一次插入操作,那么它必定不会为空.使用课本上的图,重新给这几个关键结点命名将Y的根设为k2,如下图:

我们不知道B和C是否一样高或者谁高,我们也不需要知道,但我们知道k1和k2都是满足平衡条件的并且k2的高度比A高1也就是说B和C中至少有1个和A一样高,至多有一个比A矮1;类似上面情况(1)的推理,我们还能推得A和D一样高.这样一来,我们就可以放心的开始使一切变得平衡了.根据查找树的性质和我们得出的A,B,C,D四颗子树高度的关系,如图4-38的右边部分,我们将k2作为新的根,k1和k3分别为它的左右子树,A和D的相对位置没有变,而B和C被移动到了合适的位置.这种操作可以叫做左双旋转.注意到,和情况(1)一样,这样一来这整个一颗树的高度在插入前和插入并旋转后没有发生变化,因此必然不会影响它的父节点(如果存在的话)的平衡情况.

知道怎样使AVL树保持平衡之后,就可以得出insert的算法.像一般的二叉查找树那样找到结点应该被插入的位置.然后从被插入点的父亲向上开始检查它的每个祖先,如果发现了一个不满足平衡条件的结点,立即进行”旋转”操作.如前所述,插入结点后,只要最多一次旋转就可以AVL树依然是平衡的.

下面给出两种旋转和insert操作的C++代码,这里给出情况(1)和(2)的代码,完整的代码在这里.至于insert的代码,基本就是课本上图4-42中代码,只是做了一个小小的改进.

1 void leftSingleRotation(AVLnode * &t)//左单旋转
2 {
3     AVLnode *s=t->left;
4     t->left=s->right;
5     s->right=t;
6     t->height=max(height(t->left),height(t->right))+1;//重新计算s和t的高度
7     s->height=max(height(s->left),t->height)+1;
8     t=s;
9 }

1 void leftDoubleRotation(AVLnode * &t)//左双旋转
2 {
3     AVLnode *p=t->left;
4     AVLnode *q=p->right;
5     t->left=q->right;
6     p->right=q->left;
7     q->left=p;
8     q->right=t;
9     t->height=max(height(t->left),height(t->right))+1;//重新计算3个结点的高度
10     p->height=max(height(p->left),height(p->right))+1;
11     q->height=max(p->height,t->height)+1;
12     t=q;
13 }

1 void insert(const Object &x,AVLnode * &t)
2 {
3     if(!t)
4         t=new AVLnode(x,NULL,NULL);
5     else if(x<t->data)
6     {
7         insert(x,t->left);
8         if(height(t->left)-height(t->right)==2)//在左子树插入结点后,不可能右子树比左子树高2
9             if(x<t->left->data)
10                 leftSingleRotation(t);//左单旋转
11             else
12                 leftDoubleRotation(t);//左双旋转
13         else//不需要调整就满足平衡条件的话,只需要重新计算其高度就好
14             t->height=max(height(t->left),height(t->right))+1;
15     }
16     else if(x>t->data)
17     {
18         insert(x,t->right);
19         if(height(t->right)-height(t->left)==2)
20             if(x>t->right->data)
21                 rightSingleRotation(t);//右单旋转
22             else
23                 rightDoubleRotation(t);//右双旋转
24         else
25             t->height=max(height(t->left),height(t->right))+1;
26     }
27     else;//不考虑重复的值
28 }

继续,我们来看remove(删除)操作.首先,回顾一下对于一般的二叉查找树是怎样进行remove操作的.先根据二叉树的性质找到应该删除的结点t(如果有的话);如果t是个叶子结点,直接delete就好;如果它只有一颗非空的子树,那么就让这颗子树继承被删除结点的位子;而如果它有两颗非空的子树,就在右子树X中找到值最小的结点s,将s的data(值)写到t中,再在X中删除s(因为s的左子树一定为空,否则它就不是X中最小的了.另外,当然也可以在左子树中找值最大的结点.)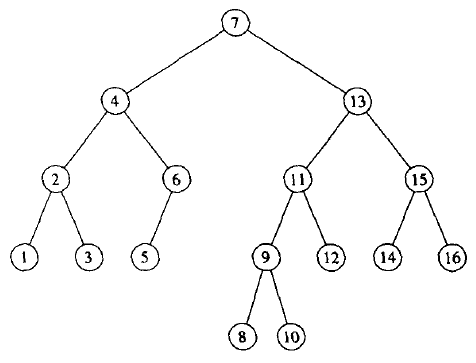

接下来,我们得仔细分析删除的时候会发生什么,在什么情况下会出现怎样的不平衡.这里我使用的是课本上在讲解insert时用到的一颗树,如右图.由于我比较懒,就不在这里画出删除结点之后的各种图形了,大家可以在纸上画,也许画着画着就想出比我的解法更好的解法了.

假设删除结点10,再删除结点12,这时候结点11就不满足平衡条件了,出现了类似情况(1)的情形.

再假设先删除结点8,再删除结点12,这时候还是结点11不平衡,但这时类似情况(2).

再假设直接删除结点12,这时依然是结点11不平衡,这时虽然和情况(1),(2)都不相同,但我们可以像图4-34那样经过一次单旋转使结点11变得平衡.(只不过这时图4-34中的Y和X一样高而不是比X矮1.)

这里特别需要注意的是,不管上上面3中情况中的哪一种情况,通过旋转使结点11平衡之后,它的高度都从2变成了1.这意味着,它的父亲的高度可能发生变化并且可能不再满足平衡条件.所以我们要从被删除点的父亲向上开始检查它的每个祖先,平衡每一个不满足平衡条件的祖先,直到找到了一个高度没有发生变化的祖先.

另外,而对于删除有一个或者两个非空子树的结点,实际上都只是删除一个叶子结点.这样一来,我们得到了remove操作可能引发不平衡的4种情况.我们假设第一个不满足平衡条件的结点为t,t的左子树为X,右子树为Y.

(1)在Y中删除了一个结点,而X的右子树不高于X的左子树.

(2)在Y中删除了一个结点,而X的右子树高于X的左子树.

(3)在X中删除了一个结点,而Y的左子树不高于Y的右子树.

(4)在X中删除了一个结点,而Y的左子树高于Y的右子树.

对于情况(1),我们可以通过一次左单旋转使t平衡;而对于情况(1),我们可以通过一次左双旋转使t平衡;而情况(3)和(4)就可能分别需要进行右单旋转和右双旋转.下面给出我的remove操作代码:

1 void AVLTree<Object>::remove(const Object &x,AVLnode *&t)
2 {
3     if(!t)return;//没有找到要删除的值,do nothing
4     if(x<t->data)
5     {
6         remove(x,t->left);
7         if(height(t->right)-height(t->left)==2)
8         {
9             //右子树比左子树高2,那么在删除操作之前右子树比左子树高1,
10             //也就是说t的右子树必然不为空,甚至必然有非空子树(高度至少为1).
11             AVLnode *s=t->right;
12             if(height(s->left)>height(s->right))
13                 rightDoubleRotation(t);//右双旋转
14             else
15                 rightSingleRotation(t);//右单旋转
16         }
17         else
18             //不需要调整就满足平衡条件的话,只需要重新计算其高度就好
19             t->height=max(height(t->left),height(t->right))+1;
20     }
21     else if(x>t->data)
22     {
23         remove(x,t->right);
24         if(height(t->left)-height(t->right)==2)
25         {
26             AVLnode *s=t->left;
27             if(height(s->right)>height(s->left))
28                 leftDoubleRotation(t);//左双旋转
29             else
30                 leftSingleRotation(t);//左单旋转
31         }
32         else
33             t->height=max(height(t->left),height(t->right))+1;
34     }
35     else
36     {
37         if(t->left&&t->right)
38         //t的左右子树都非空,把remove操作转移到只有一个非空子树的结点或者叶子结点上去
39         {
40             if(height(t->left)>height(t->right))
41             //把remove操作往更高的那颗子树上转移
42             {
43                 //左子树中的最大值
44                 t->data=max_node(t->left)->data;
45                 remove(t->data,t->left);
46             }
47             else
48             {
49                 //右子树中的最小值
50                 t->data=min_node(t->right)->data;
51                 remove(t->data,t->right);
52             }
53         }
54         else
55         {
56             AVLnode *oldnode=t;
57             t=t->left?t->left:t->right;
58             delete oldnode;
59         }
60     }
61 }

这里是我写的一个AVL的简单实现: C++实践笔记(四)----AVL树的简单实现

其中有一个粗糙的使用队列进行层次遍历打印树的代码,现在看起来如果想使对齐更完美,可以设置一个字符串最大长度的值.如果数据的长度比这个值小,就用空格补齐.

作者: Barryhe 发表于 2011-11-28 16:34 原文链接

评论: 0　查看评论　发表评论

最新新闻：
· Google雅虎等呼吁欧盟勿制订过于严格隐私法律(2011-11-28 21:06)
· 强龙难压地头蛇微软WP7俄罗斯忍痛割Bing(2011-11-28 20:27)
· 奇艺启动新域名背后：解决视听许可证遗留问题(2011-11-28 20:25)
· Kindle“黑色星期五”销量达去年同期四倍(2011-11-28 20:24)
· 维基解密本周将启动新在线系统(2011-11-28 20:21)

编辑推荐：如何快速成为Javascript高手的思考

文章来源:http://www.cnblogs.com/heqile/archive/2011/11/28/2265713.html

posted @ 2011-11-28 21:57 Barryhe 阅读(299) | 评论 (0) | 编辑收藏

[导入]C++学习笔记(八)----关于类(2)

接下来,我们根据《数据结构和算法分析 C++描述》中图3-12至3-20的代码,继续回顾类的有关知识.

代码如下:

  1 template<typename Object>
  2 class List
  3 {
  4 private:
  5     struct Node
  6     {
  7         Object  data;
  8         Node   *prev;
  9         Node   *next;
10
11         Node( const Object & d = Object( ), Node *p = NULL, Node *n = NULL )
12           : data( d ), prev( p ), next( n ) { }
13     };
14
15 public:
16     class const_iterator
17     {
18       public:
19         const_iterator( ) : current( NULL )
20           { }
21
22         const Object & operator* ( ) const
23           { return retrieve( ); }
24
25         const_iterator & operator++ ( )
26         {
27             current = current->next;
28             return *this;
29         }
30
31         const_iterator operator++ ( int )
32         {
33             const_iterator old = *this;
34             ++( *this );
35             return old;
36         }
37
38         bool operator== ( const const_iterator & rhs ) const
39           { return current == rhs.current; }
40         bool operator!= ( const const_iterator & rhs ) const
41           { return !( *this == rhs ); }
42
43       protected:
44         Node *current;
45
46         Object & retrieve( ) const
47           { return current->data; }
48
49         const_iterator( Node *p ) : current( p )
50           { }
51
52         friend class List<Object>;
53     };
54
55
56
57     class iterator : public const_iterator
58     {
59       public:
60         iterator( )
61           { }
62
63         Object & operator* ( )
64           { return retrieve( ); }
65         const Object & operator* ( ) const
66           { return const_iterator::operator*( ); }
67
68         iterator & operator++ ( )
69         {
70             current = current->next;
71             return *this;
72         }
73
74         iterator operator++ ( int )
75         {
76             iterator old = *this;
77             ++( *this );
78             return old;
79         }
80
81       protected:
82         iterator( Node *p ) : const_iterator( p )
83           { }
84
85         friend class List<Object>;
86     };
87
88 public:
89     List( )
90       { init( ); }
91
92     ~List( )
93     {
94         clear( );
95         delete head;
96         delete tail;
97     }
98
99     List( const List & rhs )
100     {
101         init( );
102         *this = rhs;
103     }
104
105     const List & operator= ( const List & rhs )
106     {
107         if( this == &rhs )
108             return *this;
109         clear( );
110         for( const_iterator itr = rhs.begin( ); itr != rhs.end( ); ++itr )
111             push_back( *itr );
112         return *this;
113     }
114
115
116
117     iterator begin()
118     {
119         return iterator(head->next);
120     }
121     const_iterator begin() const
122     {
123         return const_iterator(head->next);
124     }
125     iterator end()
126     {
127         return iterator(tail);
128     }
129     const_iterator end() const
130     {
131         return const_iterator(tail);
132     }
133
134     bool empty() const
135     {
136         return theSize==0;
137     }
138     int size() const
139     {
140         return theSize;
141     }
142
143     void clear()
144     {
145         while(!empty())
146         pop_front();
147     }
148
149     Object & front( )
150       { return *begin( ); }
151     const Object & front( ) const
152       { return *begin( ); }
153     Object & back( )
154       { return *--end( ); }
155     const Object & back( ) const
156       { return *--end( ); }
157     void push_front( const Object & x )
158       { insert( begin( ), x ); }
159     void push_back( const Object & x )
160       { insert( end( ), x ); }
161     void pop_front( )
162       { erase( begin( ) ); }
163     void pop_back( )
164       { erase( --end( ) ); }
165
166     // Insert x before itr.
167     iterator insert( iterator itr, const Object & x )
168     {
169         Node *p = itr.current;
170         theSize++;
171         return iterator( p->prev = p->prev->next = new Node( x, p->prev, p ) );
172     }
173
174     // Erase item at itr.
175     iterator erase( iterator itr )
176     {
177         Node *p = itr.current;
178         iterator retVal( p->next );
179         p->prev->next = p->next;
180         p->next->prev = p->prev;
181         delete p;
182         theSize--;
183
184         return retVal;
185     }
186
187     iterator erase( iterator start, iterator end )
188     {
189         for( iterator itr = from; itr != to; )
190             itr = erase( itr );
191
192         return to;
193     }
194
195
196   private:
197     int   theSize;
198     Node *head;
199     Node *tail;
200
201     void init( )
202     {
203         theSize = 0;
204         head = new Node;
205         tail = new Node;
206         head->next = tail;
207         tail->prev = head;
208     }
209 };

1.我们看到在第4行,Node类作为List的成员被标记为private,所以它就不能被List之外的类访问,它对用户(类的使用者)来说是隐藏的.同时,定义Node时使用了struct关键字,Node中的成员会默认为是公有的,使我们能在List及其派生类的成员函数中使用.

2.看两个构造函数,分别在第12行和89行.Node()的形参列表中有两个默认值为NULL的指针,接着通过初始化列表,next和prev成员被安全的初始化了.而在List()中,我们没有看到形参也没有看到初始化列表.这样,在List()的初始化阶段,head和tail是危险的,他们没有被初始化;但是函数体中的new语句保证了构造函数的正确性,new语句返回的地址被赋值给head和tail.

3.const_iterator类有两个构造函数,分别在第19行和第49行,其中const_iterator()是公有的,而const_iterator(Node *p)如果也被标记为public是不合适的,因为Node类对用户是隐藏的.而事实上定义这样一个构造函数就只是在List类范围内使用的.

4.关于派生类的构造函数.当系统调用第60行的默认构造函数iterator()时,会自动调用其基类的默认构造函数,用来初始化从const_iterator继承而来的成员current.如果执行下面这句代码:

List<int> lis;

List<int>::iterator iter=lis.begin();

第2句的执行过程是这样的:首先调用117行的begin()函数,然后调用其函数体中的iterator( Node *p )函数(定义在第82行),接着调用其初始化列表中的const_iterator( Node *p )函数(定义在第49行).这样构造了一个构造了一个iterator类型的临时对象,该对象的current成员的值是复制了lis的头结点的next成员的值.最后使用编译器合成的iterator类的复制构造函数将这个临时对象复制给iter.

可以同样想一想并且测试下面的语句:

List<int>::iterator iter;

是怎样执行的.

5.第25行至第36行是const_iterator类对"++"操作符的重载,我们知道"++"操作符有两个版本,分别是前缀和后缀版本,这两个版本是根据形参表中是否有一个匿名的int参数来区分的.如果形参表为空,则为前缀版本(++itr);而后缀版本(itr++)调用单参数operator++.这个int参数实际是不使用的,仅仅作为一个标识而存在.

设计const_iterator是希望有一种"自以为"指向const对象的指针,这种指针不能修改其所指向的对象,但是这种指针本身的值是可以改变的.我们看到对"++"的重载版本不是const函数,而且这个函数返回的是一般引用.似乎iterator类也可以继承这对函数,但是由于返回值类型不同,所以在iterator类的定义中我们得重新提供operator++的实现.

6.为了实现设计"const_”类的目的,我们在第22行重载”*”操作符时,返回的是const引用,这就保证了无法使用const_iterator类对象修改其所指向对象的值.

进一步探究这个函数,它是一个const函数,因为我们不打算通过它修改const_iterator类对象本身的值,所以函数体内的retrieve( )函数(定义在第46行)也必须是const函数.这是因为:const成员函数不能访问非const成员函数,反之则可以.

显然,在定义iterator类时,我们要重写operator*函数(第63行),这个函数返回一般引用,因此可以用来修改iterator对象所指向的对象的值.函数体中同样调用了retrieve()函数,如前所述,非const成员函数可以访问const成员函数,所以这是合法的.

那么为什么还要写第65,66行的代码呢?因为对于iterator类来说,由于有了修改版本的operator*函数(第63,64行),其基类中的operator*函数(第22,23行)就会被隐藏掉.这时,如果我们对一个由const关键字修饰的iterator对象解引用,编译器就会找不到可用的operator*函数.因此,第65,66行的代码是必须的.

作者: Barryhe 发表于 2011-11-02 22:24 原文链接

评论: 0　查看评论　发表评论

文章来源:http://www.cnblogs.com/heqile/archive/2011/11/02/2233669.html

posted @ 2011-11-02 22:24 Barryhe 阅读(163) | 评论 (0) | 编辑收藏

[导入]C++学习笔记(七)----关于类(1)

做了几道zoj的题目,感到基础知识都忘得差不多了,很有必要重新学习,选了两本书,一本是大学时的课本《数据结构（C语言版）》,循序渐进,由浅入深,相信学过数据结构的都看过或者听说过这本书.还有一本是在网上找到的,书名是《数据结构和算法分析 C++描述》,这本书文字比较简练,但其中包含的信息量很大,读起来很有味道,也让人很有激情,很好.

现在分析一下《数据结构和算法分析 C++描述》中图3-7,3-8的代码,看看能从这段代码中找到哪些需要注意的要点.

代码如下:

1 template <typename Object>
2 class Vector
3 {
4   public:
5     explicit Vector( int initSize = 0 )
6       : theSize( initSize ), theCapacity( initSize + SPARE_CAPACITY )
7       { objects = new Object[ theCapacity ]; }
8     Vector( const Vector & rhs ) : objects( NULL )
9       { operator=( rhs ); }
10     ~Vector( )
11       { delete [ ] objects; }
12
13     const Vector & operator= ( const Vector & rhs )
14     {
15         if( this != &rhs )
16         {
17             delete [ ] objects;
18             theSize = rhs.size( );
19             theCapacity = rhs.theCapacity;
20
21             objects = new Object[ capacity( ) ];
22             for( int k = 0; k < size( ); k++ )
23                 objects[ k ] = rhs.objects[ k ];
24         }
25         return *this;
26     }
27
28     void resize( int newSize )
29     {
30         if( newSize > theCapacity )
31             reserve( newSize * 2 + 1 );
32         theSize = newSize;
33     }
34
35     void reserve( int newCapacity )
36     {
37         if( newCapacity < theSize )
38             return;
39
40         Object *oldArray = objects;
41
42         objects = new Object[ newCapacity ];
43         for( int k = 0; k < theSize; k++ )
44             objects[ k ] = oldArray[ k ];
45
46         theCapacity = newCapacity;
47
48         delete [ ] oldArray;
49     }
50
51
52     Object & operator[]( int index )
53       { return objects[ index ]; }
54     const Object & operator[]( int index ) const
55       { return objects[ index ]; }
56
57     bool empty( ) const
58       { return size( ) == 0; }
59     int size( ) const
60       { return theSize; }
61     int capacity( ) const
62       { return theCapacity; }
63
64     void push_back( const Object & x )
65     {
66         if( theSize == theCapacity )
67             reserve( 2 * theCapacity + 1 );
68         objects[ theSize++ ] = x;
69     }
70
71     void pop_back( )
72       { theSize--; }
73
74     const Object & back ( ) const
75       { return objects[ theSize - 1 ]; }
76
77     typedef Object * iterator;
78     typedef const Object * const_iterator;
79
80     iterator begin( )
81       { return &objects[ 0 ]; }
82     const_iterator begin( ) const
83       { return &objects[ 0 ]; }
84     iterator end( )
85       { return &objects[ size( ) ]; }
86     const_iterator end( ) const
87       { return &objects[ size( ) ]; }
88
89     enum { SPARE_CAPACITY = 16 };
90
91   private:
92     int theSize;
93     int theCapacity;
94     Object * objects;
95 };

1.第1行,template ['templit]关键字后接模板形参表,表明这里定义的Vector是一个类模板,而不是一个类,Vector<int>才是一个类.函数模板也是一样,它们都只是一个"公式".

2.第5行,将构造函数声明为explicit [ik'splisit] ,是为了抑制由构造函数定义的隐式转换,如果这里没有explicit,那么下面的语句:

Vector vec;

...

vec=2;

将是合法的,"="右边的2将被这个不带explicit的构造函数隐式转换为一个Vector类型的临时变量,然后再通过operator=复制给vec.但这可能不是我们想要的结果,为了避免错误,在某些情况下,我们给单形参构造函数加上关键字explicit,这样的话上面的语句就不能编译通过了,vec=2要改为vec=vec(2).关于explicit的更多论述,可以参见《C++ Primer》第12.4.4小节.

3.第6行,是构造函数的初始化列表.关于构造函数的初始化列表,有两个要点.第一,即使列表为空,没有初始化式,构造函数也会先初始化每个成员再进入函数体,这时初始化的规则与初始化变量相同,由此得知第二个要点:如果类的成员本身是一个没有默认构造函数的类类型,或者成员是const、引用类型,这样的成员必须在构造函数初始化列表中进行初始化.详见《C++ Primer》第12.4.1小节.

4.第7行和第11行,第7行的new返回一个指向Object类型数组的指针,而通过new关键字分配的存储空间需要通过delete操作将其删除.反之,如果某个对象不是通过new操作动态创建获得的,那么它就不能由delete操作释放,事实上在这些对象的生命期结束之后,编译器会自动释放空间.这两行是一个特例,他们不是动态创建和释放单个对象,而是动态创建和释放数组,所以我们看到第11行使用了"delete []"操作符.

5.第8行至第26行分别定义了Vector的复制构造函数,析构函数和重载赋值操作符.

6.第52至55行,这里定义了重载下标操作符的两个版本,由于成员函数的定常性是(即函数名后是否有const关键字)是签名的一部分,因此我们可以使用访问函数的operator[]版本返回const引用,而修改函数版本返回一般引用.

作者: Barryhe 发表于 2011-10-31 14:45 原文链接

评论: 7　查看评论　发表评论

文章来源:http://www.cnblogs.com/heqile/archive/2011/10/31/2230271.html

posted @ 2011-10-31 14:45 Barryhe 阅读(165) | 评论 (0) | 编辑收藏

[导入]zoj1005

#include <vector>
#include <iostream>
#include <string>
using namespace std;

vector<int> vec;
int flag=0,ca,cb,n;
void find(int x,int y)
{
    if(x==ca&&y==0){vec.push_back(-2);return;}
    if(x==0&&y==cb){vec.push_back(-3);return;}
    if(x!=ca&&y!=0&&flag!=-1)
    {
        vec.push_back(1);
        flag=1;
        int rem=y-ca+x;
        if(rem>0)
            find(ca,rem);
        else
            find(x+y,0);
    }
    else if(y!=cb&&x!=0&&flag!=1)
    {
        vec.push_back(-1);
        flag=-1;
        int rem=x-cb+y;
        if(rem>0)
            find(rem,cb);
        else
            find(0,x+y);
    }
   else if(x==0&&flag!=-2)
    {
        vec.push_back(2);
        flag=2;
        find(ca,y);
    }
    else if(x==ca&&flag!=2)
    {
        vec.push_back(-2);
        flag=-2;
        find(0,y);
    }
    else if(y==0&&flag!=-3)
    {
        vec.push_back(3);
        flag=3;
        find(x,cb);
    }
    else if(y==cb&&flag!=3)
    {
        vec.push_back(-3);
        flag=-3;
        find(x,0);
    }
    return;
}
void print(int f)
{
    string str;
    switch(f)
    {
    case 1:
        str="pour A B";
        break;
    case -1:
        str="pour B A";
        break;
    case -2:
        str="fill A";
        break;
    case 2:
        str="empty A";
        break;
    case -3:
        str="fill B";
        break;
    case 3:
        str="empty B";
    }
    cout<<str<<endl;
}
int main()
{
    while(cin>>ca>>cb>>n)
    {
        find(0,n);
        for(vector<int>::reverse_iterator riter=vec.rbegin();riter!=vec.rend();riter++)
            if(--riter.base()!=vec.begin()||*riter!=2)print(*riter);
        cout<<"success"<<endl;
        vec.clear();
    }
    return 0;
}

终于给力了一把,第一次submit就AC了.

恩,继续继续~~

作者: Barryhe 发表于 2011-10-25 17:15 原文链接

评论: 0　查看评论　发表评论

文章来源:http://www.cnblogs.com/heqile/archive/2011/10/25/2224175.html

posted @ 2011-10-25 17:15 Barryhe 阅读(141) | 评论 (0) | 编辑收藏

[导入]zoj1002

#include <vector>
#include <iostream>
using namespace std;
int length,ops;
vector<vector<int> > city;
int openCount(int x,int y)
{
    int co=0;
    if(x>0&&city[x-1][y]!=0)co++;
    if(y>0&&city[x][y-1]!=0)co++;
    if(x<length-1&&city[x+1][y]!=0)co++;
    if(y<length-1&&city[x][y+1]!=0)co++;
    return co;
}
void setFlag(int x,int y)
{
    for(int s=x-1;s>=0;s--)
    {
        if(city[s][y]==0)break;
        else if(city[s][y]!=-2) {city[s][y]=-2;ops--;}
    }
    for(int s=y-1;s>=0;s--)
    {
        if(city[x][s]==0)break;
        else if(city[x][s]!=-2) {city[x][s]=-2;ops--;}
    }
    for(int s=x+1;s<length;s++)
    {
        if(city[s][y]==0)break;
        else if(city[s][y]!=-2) {city[s][y]=-2;ops--;}
    }
    for(int s=y+1;s<length;s++)
    {
        if(city[x][s]==0)break;
        else if(city[x][s]!=-2) {city[x][s]=-2;ops--;}
    }
}
int getFlag(int x,int y)
{
    int co=0;
    for(int s=x-1;s>=0;s--)
    {
        if(city[s][y]==0)break;
        else co++;
    }
    for(int s=y-1;s>=0;s--)
    {
        if(city[x][s]==0)break;
        else co++;
    }
    for(int s=x+1;s<length;s++)
    {
        if(city[s][y]==0)break;
        else co++;
    }
    for(int s=y+1;s<length;s++)
    {
        if(city[x][s]==0)break;
        else co++;
    }
    return co;
}
int main()
{
    while(cin>>length&&length!=0)
    {
    char c;
    ops=0;
    if(length==1)
    {
        cin>>c;
        if(c=='.')cout<<"1"<<endl;
        else cout<<"0"<<endl;
    }
    else
    {
        city.clear();
        city.resize(length,vector<int>(length));
        int count=0;
        int min_open,min_fl;
        int opc=0,flag=0;
        int x,y;
        for(int i=0;i<length;i++)
            for(int j=0;j<length;j++)
            {
                cin>>c;
                if(c=='.'){city[i][j]=1;ops++;}
                else city[i][j]=0;
            }
        while(ops!=0)
        {
            min_open=5;
            min_fl=16;
            for(int i=0;i<length;i++)
                for(int j=0;j<length;j++)
                {
                    if(city[i][j]==1)
                    {
                        opc=openCount(i,j);
                        flag=getFlag(i,j);
                        if((opc<min_open)||(opc==min_open&&flag<min_fl))
                        {min_fl=flag;min_open=opc;x=i;y=j;}
                    }
                }
            city[x][y]=-1;
ops--;
count++;
setFlag(x,y);
        }
        cout<<count<<endl;
    }
    }
    return 0;
}

虽然终于AC过去了,但其实还是失败的,因为我都不能证明自己的算法是正确的...大学时学得真是忘得差不多了,要好好补补算法的基础知识了~~下次写个心中有数的算法再AC一次!

I'm back!

作者: Barryhe 发表于 2011-10-21 15:15 原文链接

评论: 0　查看评论　发表评论