卷积的介绍
卷积(convolution)是泛函分析里的一个概念,不过泛函分析一般都是数学系才学的,计算机系的学生大多在概率统计课本里了解到。它分为两种形式,一个是离散形式,一个是连续(积分)形式。在图像处理中我们更关心离散卷积,不过也先看看积分形式的卷积。现在假设我们有两个函数 和
和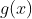 ,这里
,这里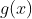 又叫做平滑函数或者卷积核,那么它们在连续空间的卷积是:
又叫做平滑函数或者卷积核,那么它们在连续空间的卷积是:
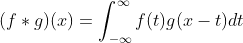
一般我们有一个这样的结论,就是当 经过足够多次相同平滑函数
经过足够多次相同平滑函数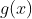 卷积,就会足够接近高斯函数,也就是正态分布的函数形式。卷积就是一种平滑操作,这说明高斯函数就是“最平滑的函数”。引入热力学中熵的概念,高斯函数就是拥有最高熵的函数,最稳定的状态,以至于自然界大多数的统计规律都呈现出正态分布:
卷积,就会足够接近高斯函数,也就是正态分布的函数形式。卷积就是一种平滑操作,这说明高斯函数就是“最平滑的函数”。引入热力学中熵的概念,高斯函数就是拥有最高熵的函数,最稳定的状态,以至于自然界大多数的统计规律都呈现出正态分布:
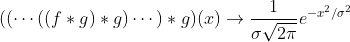
下面介绍离散形式的卷积。这卷积,首先是由有限项的多项式体现。神奇的是,而它们的乘积就是卷积。首先我们设有两个多项式 以及
以及 。计算它们的乘积:
。计算它们的乘积:
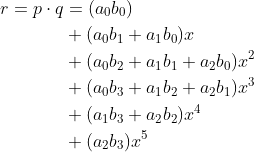
再引入离散形式卷积(向量卷积)的定义,大家比较一下这个定义和上面多项式的计算。稍微说明一下,中括号的意义是p[n]代表向量第n个元素。将两个多项式的系数写成向量形式然后进行向量卷积,也就是例如![p = [a_0, a_1, a_2]](http://latex.codecogs.com/gif.latex?p%20=%20%5Ba_0,%20a_1,%20a_2%5D) ,而没定义的地方当作0。可以发现,两者是完全一致的:
,而没定义的地方当作0。可以发现,两者是完全一致的:
![\begin{align*} (p * q)[n] &= \sum_{m=-\infty}^\infty p[m]\cdot q[n-m] \\ r[1] &= \sum_{m=0}^1 p[m]\cdot q[1-m] &&= a_0 b_1 + a_1 b_0 \\ r[2] &= \sum_{m=0}^2 p[m]\cdot q[2-m] &&= a_0 b_2 + a_1 b_1 + a_2 b_0 \\ &\cdots \end{align*}](http://latex.codecogs.com/gif.latex?%5Cbegin%7Balign*%7D%0A%28p%20*%20q%29%5Bn%5D%20&=%20%5Csum_%7Bm=-%5Cinfty%7D%5E%5Cinfty%20p%5Bm%5D%5Ccdot%20q%5Bn-m%5D%20%5C%5C%0Ar%5B1%5D%20&=%20%5Csum_%7Bm=0%7D%5E1%20%20p%5Bm%5D%5Ccdot%20q%5B1-m%5D%20&&=%20a_0%20b_1%20+%20a_1%20b_0%20%5C%5C%0Ar%5B2%5D%20&=%20%5Csum_%7Bm=0%7D%5E2%20%20p%5Bm%5D%5Ccdot%20q%5B2-m%5D%20&&=%20a_0%20b_2%20+%20a_1%20b_1%20+%20a_2%20b_0%20%5C%5C%0A&%5Ccdots%0A%5Cend%7Balign*%7D)
知道了多项式的乘积就是其相应的卷积,我们甚至可以直接得出两个幂级数卷积的结果。因为泰勒级数就是幂级数的一种,所以我们可以将几乎所有的连续函数转换成离散形式,避免了繁复的积分运算:比如我们希望得到 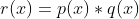 ,其中
,其中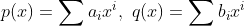 ,只需要简单地计算这两个级数的柯西乘积,所得结果就是
,只需要简单地计算这两个级数的柯西乘积,所得结果就是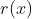 的卷积。当然了,这是后话,与本文的主题无关。
的卷积。当然了,这是后话,与本文的主题无关。
卷积与图像处理
在开始讲图像处理之前,我希望先理解一下卷积的整个过程是怎样的。从上面的公式看得还是有点懵懵懂懂,从直觉上去理解一下很有必要。观察卷积的公式以及下面的图片,这个过程可以看作,当你想求一个r[n]的时候:
你先把卷积核q叠在p上面,尽量使左端靠近(如果左对齐就再好不过了),然后看看在[0, n]内p, q重叠的部分是从哪里到哪里,分别写成向量,那么r[n]就等于其中一个向量与另一个向量的逆序的内积。
比如当n = 2时,两个向量是[a_0, a_1, a_2]和[b_2, b_1, b_0];n = 4时,两个向量是[a_1, a_2, a_3, a_4]和[b_3, b_2, b_1, b_0]。至于求内积,一定难不倒你。下图说明了这一点:
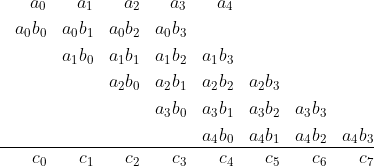
上面是对某一点上卷积的理解。对整个域的卷积,则可以看成是将卷积核(除了开头几个外)不停向右移动,每移动一格就将重叠部分拿出来求内积。
这时我们可以把图像处理和卷积联系起来了。图像处理是,将一副“源图像”(Source),通过一些算法,变成一副“目标图像”(Destination)。当我们进行平滑处理的时候,用到一个叫做滤波器(filter)的 东西,也叫做滤镜。想想我们现实生活中放大镜是怎么用的:拿着放大镜,从报纸的左上角开始,一直扫啊扫到右下角,扫的过程中一直望着放大镜和报纸的重叠区 域(其实就是望着放大镜,因为它比报纸小多了),这样你就浏览完了一张放大过的报纸。平滑滤镜也是同样的使用方法,从源图的左上角开始扫到右下角,扫的过 程中一直取出重叠部分进行内积计算,然后将结果存放到目标图像中 —— 显然这个操作跟卷积是一致的,只不过定义在二维空间内。
为了方便量化表示,我们把图像抽象成定义在![R \cap [0, 1]](http://latex.codecogs.com/gif.latex?R%20%5Ccap%20%5B0,%201%5D) 数环内的二维矩阵,其意义是灰度值,颜色信息我们暂且忽略。卷积核,也就是滤波器同样也是定义在
数环内的二维矩阵,其意义是灰度值,颜色信息我们暂且忽略。卷积核,也就是滤波器同样也是定义在![R \cap [0, 1]](http://latex.codecogs.com/gif.latex?R%20%5Ccap%20%5B0,%201%5D) 内的二维矩阵。这样,二维的卷积我们这样定义它的离散形式:
内的二维矩阵。这样,二维的卷积我们这样定义它的离散形式:
![\text{Dest}[i, j] = \sum_{y=-\infty}^\infty \sum_{x=-\infty}^\infty \text{Src}[y,x] \cdot \text{Ker}[i - y, j - x]](http://latex.codecogs.com/gif.latex?%5Ctext%7BDest%7D%5Bi,%20j%5D%20=%20%5Csum_%7By=-%5Cinfty%7D%5E%5Cinfty%20%5Csum_%7Bx=-%5Cinfty%7D%5E%5Cinfty%20%5Ctext%7BSrc%7D%5By,x%5D%20%5Ccdot%20%5Ctext%7BKer%7D%5Bi%20-%20y,%20j%20-%20x%5D)
我们的卷积核大小并不是无限的,它一个半径r,这样它的大小就是2r+1。规定了这个r使得,当|x| > r 或 |y| > r,都有Ker[y, x] = 0。规定过大小之后,由 |i-y| < r; |j-x| < r得到 i-r < y < i+r; j-r < x < j+r。同时我们规定Dest和Src的大小是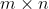 。于是我们得到了滤波器的算法:
。于是我们得到了滤波器的算法:
![\text{Dest}[i, j] = \sum_{y=\max\{0,i-r\}}^{\min\{i+r,n\}} \left( \sum_{x=\max\{0,j-r\}}^{\min\{j+r,m\}} \text{Src}[y, x] \cdot \text{Ker}[i - y, j - x] \right)](http://latex.codecogs.com/gif.latex?%5Ctext%7BDest%7D%5Bi,%20j%5D%20=%20%5Csum_%7By=%5Cmax%5C%7B0,i-r%5C%7D%7D%5E%7B%5Cmin%5C%7Bi+r,n%5C%7D%7D%20%5Cleft%28%20%5Csum_%7Bx=%5Cmax%5C%7B0,j-r%5C%7D%7D%5E%7B%5Cmin%5C%7Bj+r,m%5C%7D%7D%20%5Ctext%7BSrc%7D%5By,%20x%5D%20%5Ccdot%20%5Ctext%7BKer%7D%5Bi%20-%20y,%20j%20-%20x%5D%20%5Cright%29)
高斯滤波器

二维的高斯函数(俗称避孕套函数)
高斯滤波器是最常用的平滑滤波器之一,在Photoshop里面它被用作高斯模糊滤镜。高斯滤波器的定义很经典,就是简单地把正态分布离散开来。二维形式只是单纯把x替代成(x2 + y2),然后修改系数令实数域上的积分为1:
![\begin{align*} \text{Ker}_1[x] &= \frac 1{\sigma\sqrt{2\pi}} e^{-x^2/{\sigma^2}} \\ \text{Ker}_2[i, j] &= \frac 1{2\sigma^2\pi} e^{-(i^2+j^2)/{\sigma^2}} \end{align*}](http://latex.codecogs.com/gif.latex?%5Cbegin%7Balign*%7D%0A%5Ctext%7BKer%7D_1%5Bx%5D%20&=%20%5Cfrac%201%7B%5Csigma%5Csqrt%7B2%5Cpi%7D%7D%20e%5E%7B-x%5E2/%7B%5Csigma%5E2%7D%7D%20%5C%5C%0A%5Ctext%7BKer%7D_2%5Bi,%20j%5D%20&=%20%5Cfrac%201%7B2%5Csigma%5E2%5Cpi%7D%20e%5E%7B-%28i%5E2+j%5E2%29/%7B%5Csigma%5E2%7D%7D%0A%5Cend%7Balign*%7D)
也许你已经发现了一个这样的规律,这一规律,这在更高维上仍然是满足的,也就是在连续空间里同样满足。这将成为我们优化算法的关键。将这个规律代回到二维离散卷积的公式里,因为y在第二个连加中相当于常数系数可以提出来,我们发现:
![\begin{align*} \text{Ker}_2[i, j] &= \text{Ker}_1[i] \cdot \text{Ker}_1[j] \\ \text{Dest}[i, j] &= \sum_{y=-\infty}^\infty \sum_{x=-\infty}^\infty \text{Src}[y,x] \cdot \text{Ker}_2[i - y, j - x] \\ &= \sum_{y=-\infty}^\infty \sum_{x=-\infty}^\infty \text{Src}[y,x] \cdot \text{Ker}_1[i-y] \cdot \text{Ker}_1[j-x]\\ &= \sum_{y=-\infty}^\infty \left( \sum_{x=-\infty}^\infty \text{Src}[y,x] \cdot \text{Ker}_1[j-x]\right) \text{Ker}_1[i-y] \end{align*}](http://latex.codecogs.com/gif.latex?%5Cbegin%7Balign*%7D%0A%5Ctext%7BKer%7D_2%5Bi,%20j%5D%20&=%20%5Ctext%7BKer%7D_1%5Bi%5D%20%5Ccdot%20%5Ctext%7BKer%7D_1%5Bj%5D%20%5C%5C%0A%5Ctext%7BDest%7D%5Bi,%20j%5D%20&=%20%5Csum_%7By=-%5Cinfty%7D%5E%5Cinfty%20%5Csum_%7Bx=-%5Cinfty%7D%5E%5Cinfty%20%5Ctext%7BSrc%7D%5By,x%5D%20%5Ccdot%20%5Ctext%7BKer%7D_2%5Bi%20-%20y,%20j%20-%20x%5D%20%5C%5C%0A&=%20%5Csum_%7By=-%5Cinfty%7D%5E%5Cinfty%20%5Csum_%7Bx=-%5Cinfty%7D%5E%5Cinfty%20%5Ctext%7BSrc%7D%5By,x%5D%20%5Ccdot%20%5Ctext%7BKer%7D_1%5Bi-y%5D%20%5Ccdot%20%5Ctext%7BKer%7D_1%5Bj-x%5D%5C%5C%0A&=%20%5Csum_%7By=-%5Cinfty%7D%5E%5Cinfty%20%5Cleft%28%20%5Csum_%7Bx=-%5Cinfty%7D%5E%5Cinfty%20%5Ctext%7BSrc%7D%5By,x%5D%20%5Ccdot%20%5Ctext%7BKer%7D_1%5Bj-x%5D%5Cright%29%20%5Ctext%7BKer%7D_1%5Bi-y%5D%0A%5Cend%7Balign*%7D)
如果x连加所表示是卷积是从右上角开始按照文字书写顺序从左到右,然后从上到下的顺序进行一维卷积,那么y连加表示的卷积就是先从上到下,再从左到有的顺序卷积。在OpenCV提供的数据结构的基础上,不用imgproc提供的算法,我写了一个示例:
1 // cflags: -lopencv_highgui -lopencv_core
2
3 #include <iostream>
4 #include <cmath>
5 #include <opencv2/highgui/highgui.hpp>
6
7 using namespace cv;
8 using namespace std;
9
10 const char* title = "gaussian-filter";
11
12 Mat kernelMatrix(int radius, double sigma)
13 {
14 int d = radius * 2 + 1;
15 Mat kernel(2, d, CV_64F);
16
17 double coef = 0;
18 for(int i = 0; i <= radius; i++) {
19 // f(x) = 1/(sigma * sqrt(2 pi)) * e ^ -x^2/(2 s^2)
20 int dx = i - radius;
21 double dx_2 = dx * dx;
22 double w = pow(M_E, - dx_2 / (2 * sigma * sigma));
23
24 coef += w;
25 kernel.at<double>(0, i) = w;
26 kernel.at<double>(0, d - i - 1) = w;
27 // when you used values from i to j (j>i), the sum of them is:
28 // kernel[1, j] - (i ? kernel[1, i-1] : 0)
29 kernel.at<double>(1, i) = coef;
30 }
31
32 for(int i = radius + 1; i < d; i++) {
33 coef += kernel.at<double>(0, i);
34 kernel.at<double>(1, i) = coef;
35 }
36
37 return kernel;
38 }
39
40
41 void convolution(const Mat& img, const Mat& kernel, Mat& output, bool t = true)
42 {
43 for(int y = 0, x = 0; y < img.rows; x = (++x<img.cols)? x : (y++, 0)) {
44 Vec3d r(0, 0, 0);
45
46 int ideal = x - int(kernel.cols / 2),
47 ran_beg = max(ideal, 0) - ideal,
48 ran_end = min(ideal + kernel.cols, img.cols) - ideal;
49
50 for(int i = ran_beg; i < ran_end; i++) {
51 double weight = kernel.at<double>(0, i);
52 Vec3b pixel = img.at<Vec3b>(y, ideal + i);
53
54 r[0] += pixel[0] * weight;
55 r[1] += pixel[1] * weight;
56 r[2] += pixel[2] * weight;
57 }
58
59 double coef = kernel.at<double>(1, ran_end - 1);
60 if(ran_beg) coef -= kernel.at<double>(1, ran_beg - 1);
61
62 output.at<Vec3b>(t?x:y, t?y:x) = Vec3b(
63 saturate_cast<uchar>(r[0]/coef),
64 saturate_cast<uchar>(r[1]/coef),
65 saturate_cast<uchar>(r[2]/coef));
66 }
67 }
68
69
70 int main()
71 {
72 namedWindow(title, WINDOW_AUTOSIZE);
73
74 const int r = 10;
75
76 Mat img = imread("ai-sample.jpg"),
77 kernel = kernelMatrix(r, (r - 1) * 0.3 + 0.8);
78
79 Mat product_v = Mat(img.cols, img.rows, img.type());
80 Mat product_h = Mat(img.rows, img.cols, img.type());
81
82 convolution(img, kernel, product_v);
83 convolution(product_v, kernel, product_h);
84
85 imshow(title, product_h);
86 for(; waitKey(0) > 0;);
87
88 destroyWindow(title);
89 }
